7.3.Нечеткая нс tsk

Рассмотренные модели нечеткого вывода Мамдани–Заде и TSK с выходными сигналами (7.17) и (7.21) позволяют с произвольной точностью аппроксимировать любую функцию многих переменных суммой нечетких функций одной переменной. Формулы (7.17), (7.21), (7.22) имеют модульную структуру, идеально соответствующую многослойной НС, характерной особенностью которой является возможность использования нечетких правил вывода для расчета выходного сигнала. Обучение таких нечетких НС сводится к подбору параметров функции фаззификации.

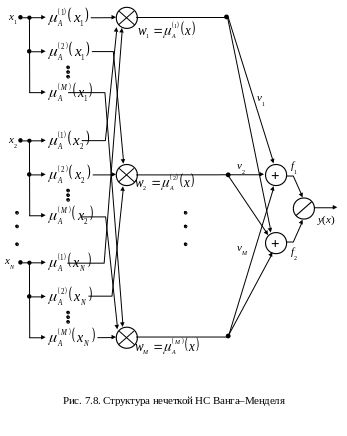
Определим структуру нечеткой сети TSK, для которой при N переменных и М правилах справедливы (7.21), (7.22), используя в качестве фаззификатора обобщенную функцию Гаусса вида (7.8) для каждой переменной x_i, в результате чего для каждого k–го правила вывода

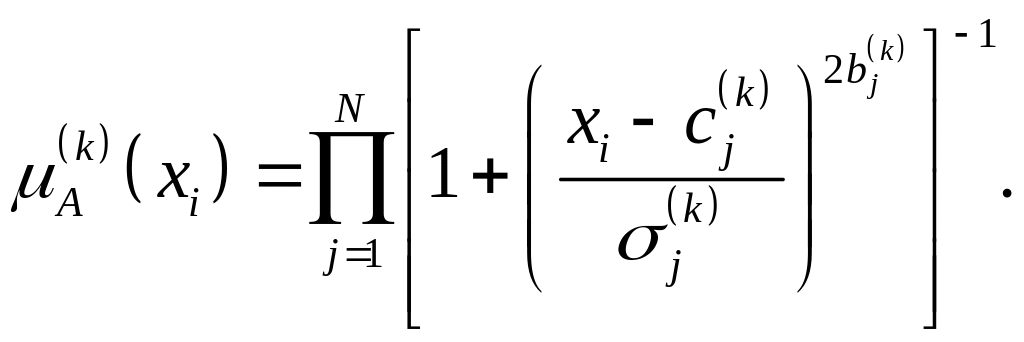(7.23)

Если веса w_i в выражении (7.21) интерпретировать как значимость компонентов , определенных (7.23), то формулам (7.21)–(7.23) можно сопоставить многослойную НС (рис. 7.7) из пяти слоев:

• первый слой выполняет фаззификацию каждой переменной, определяя для каждого k–го правила, в которой параметры 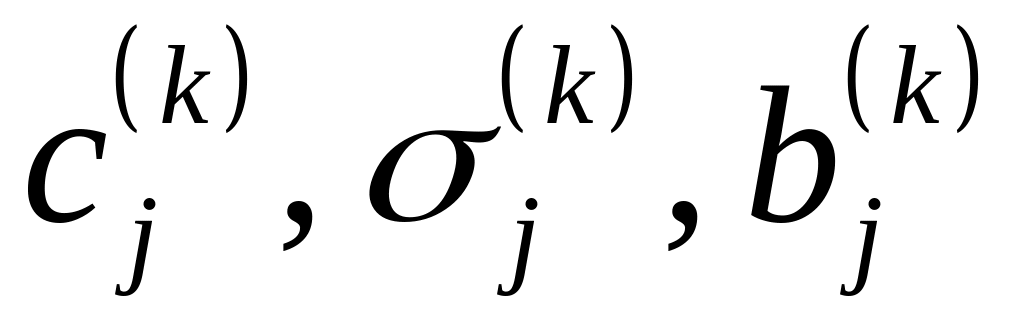определяются в процессе обучения;

• второй слой выполняет агрегирование отдельных переменных x_i, определяя результирующее значение 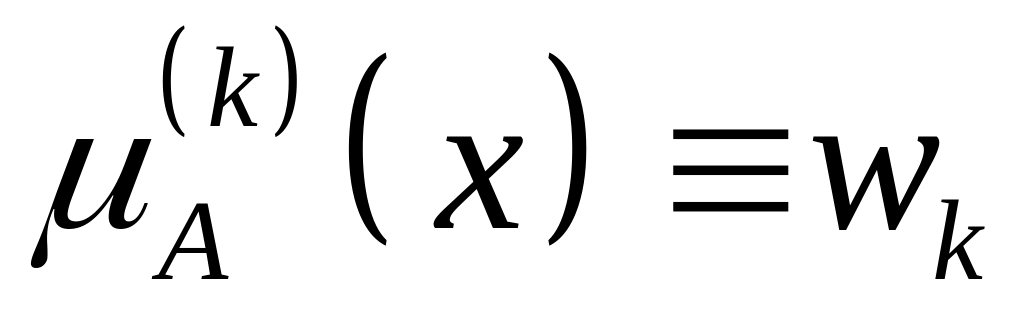в соответствии с (7.23);

• третий слой – генератор функции TSK, рассчитывающий значения y_k(x) согласно (7.22), где адаптации подлежат линейные веса p_kj для k=1, 2, …, M и j=1, 2, …, N;

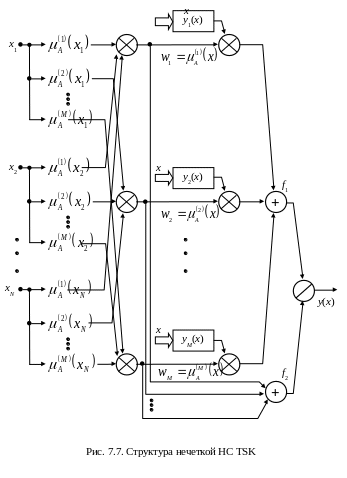
• четвертый слой составляют два нейрона – сумматора: один для взвешенной суммы y_k(x), второй – для суммы весов ;

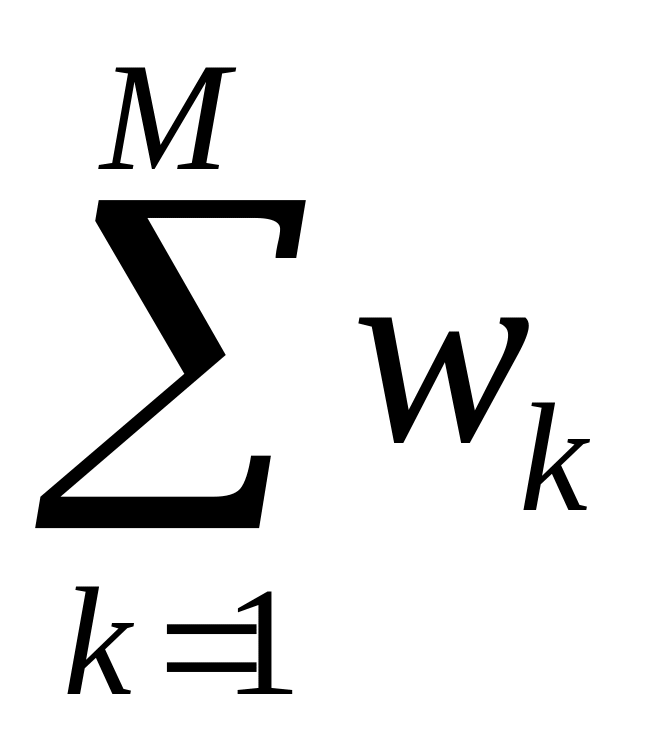• пятый слой, состоящий из одного нейрона, – нормализующий веса согласно формуле (7.21) и формирующий выходной сигнал y(x).

Таким образом, в процессе обучения НС TSK уточнению подлежат 3MN параметров первого (нелинейного) и M(N+1) третьего (линейного) слоев, что в сумме дает M(4N+1) величин. На практике для уменьшения числа адаптируемых параметров оперируют меньшим числом независимых функций принадлежности.

Частным случаем НС TSK является четырехслойная НС Ванга–Менделя (рис. 7.8) с аппроксимацией y=f(x) полиномом нулевого порядка (7.20) и результирующим выражением для y(x) типа (7.17), вытекающим из модели Мамдани–Заде. В структуре рис. 7.8 параметрическими также являются первый ( ) и третий (веса v₁, v₂, …, v_M) слои, где v_k интерпретируются как центры c_k функций принадлежности следствия k–го нечеткого правила вывода.

Заметим, что все вышеперечисленные рассуждения могут быть обобщены на случай нечетких НС с несколькими выходами.

7.4.Обучение нс с нечеткой логикой

Подобно классическим, обучение нечетких НС может проводиться либо с учителем на основе минимизации целевой функции вида (2.24), либо на основе алгоритмов самоорганизации, выполняющих группирование (кластеризацию) входных данных. Наиболее эффективным способом обучения нечетких НС считается гибридный алгоритм, в котором подлежащие адаптации параметры разделяются на 2 группы: линейных параметров p_ij 3–го слоя и параметров нелинейной функции принадлежности 1–го слоя. В соответствии с этим обучение НС проводится в 2 этапа (рассуждения справедливы как для сети TSK, так и Ванга–Менделя):

• для известных значений параметров функции принадлежности из (7.21), (7.22) при

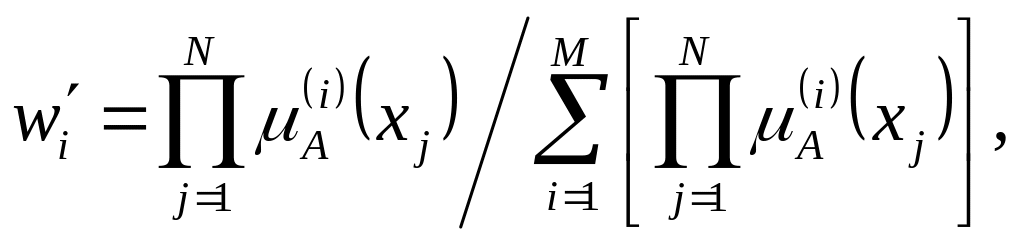(i=1, 2, …, M) (7.24)

и р обучающих выборках (k=1, 2, …, p) получают систему линейных уравнений вида

(7.25)

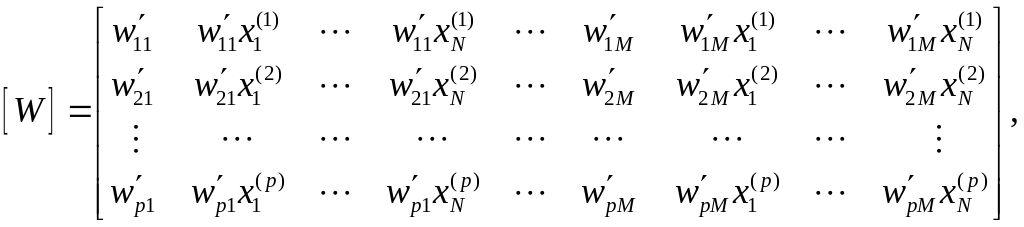
где – уровень активации (вес) i–го правила при предъявлении k–го входного . Решение (7.25) можно получить за один шаг при помощи псевдоинверсии матрицы [W], количество строк которой р обычно значительно больше количества столбцов M(N+1), т.е.

(7.26)

где нахождение [W]⁺ соответствует задаче минимизации min||[W]⁺[W]–[E]||, [E] – единичная матрица;

• при фиксированных значениях p_ij (i=1, 2, …, M) рассчитывают фактические выходные сигналы y_k­ (k=1, 2, …, p) 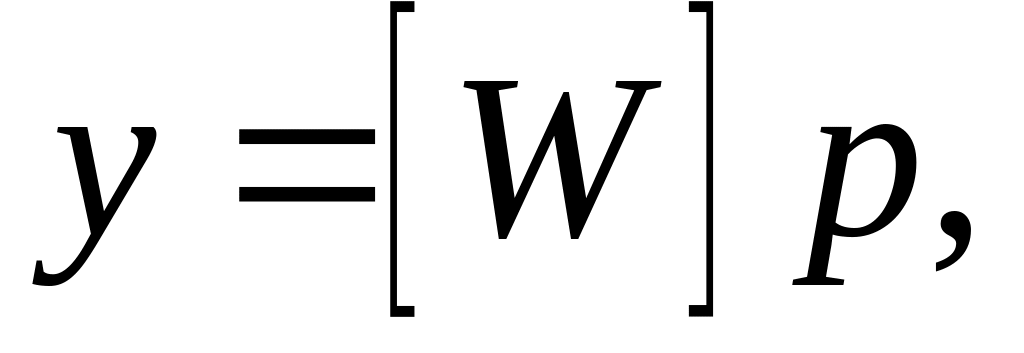вектор ошибки 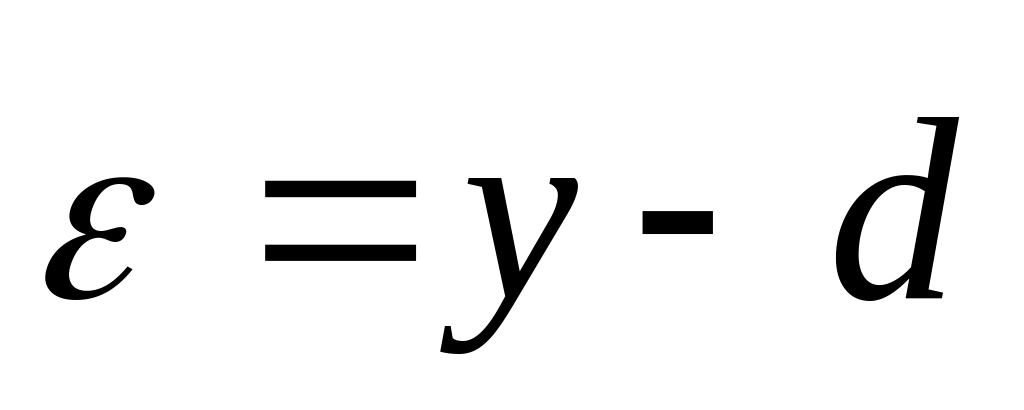и градиент целевой функции E(W) по параметрам 1–го слоя (с помощью метода ОРО). Если для обучения используют простейший из градиентных алгоритмов – АНС, то формулы адаптации принимают вид

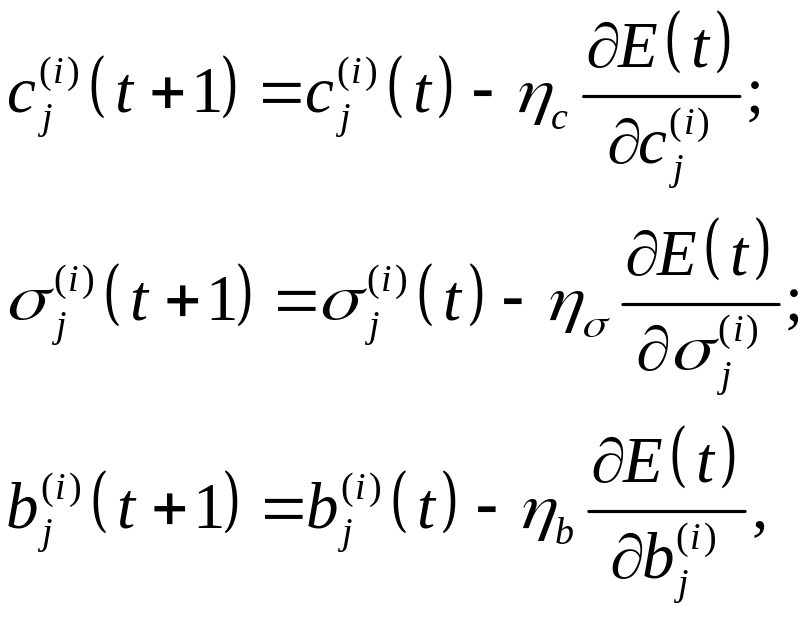(7.27)

где t – номер итерации.

После уточнения нелинейных параметров процесс адаптации возвращают к первому, затем второму этапу и т.д., повторяя цикл до стабилизации всех параметров сети. При практической реализации этого метода основным считается первый этап (определение p_ij), для компенсации его влияния второй этап (подбор нелинейных параметров градиентным методом) многократно повторяется в каждом цикле.

Алгоритмы СО используют обучение конкурентного типа аналогично НС Кохонена, определяя положение центров с_i для кластеров, на которые разделяется пространство входных данных. Среди методов СО для обучения нечетких НС наиболее известны алгоритмы С–means и Густавсона–Кесселя, отличающиеся только понятием расстояния между входными векторами, так что рассмотрим лишь первый из них.

Пусть нечеткая НС с функцией фаззификации в виде обобщенной функции Гаусса (7.8) содержит К нейронов с центрами в точках (i = 1, 2, …K), случайно выбранных из областей допустимых значений так, что степень их принадлежности u_ij[0,1] кластерам подчинена очевидному условию

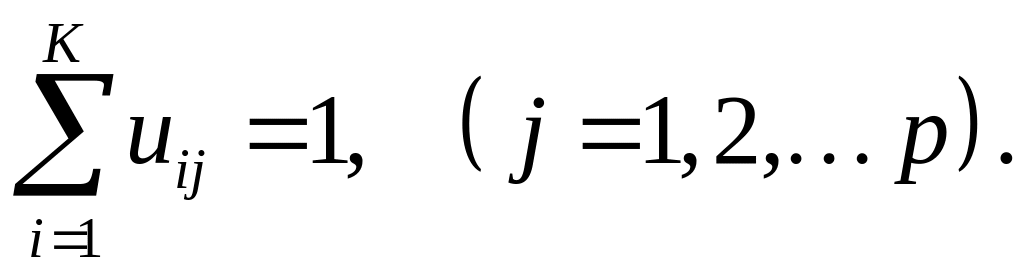(7.28)

Соответствующая такому представлению функция погрешности примет вид

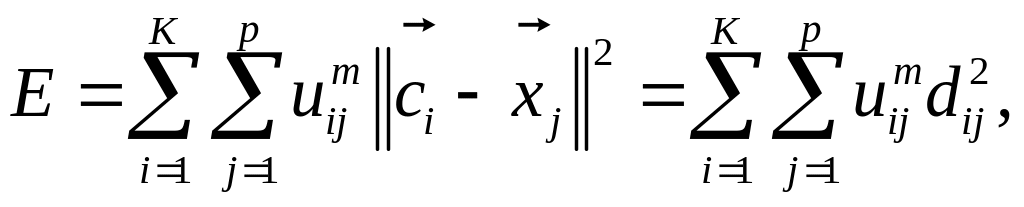(7.29)

где m[1, ) – весовой коэффициент, т.е. задача обучения с СО сводится к минимизации нелинейной функции (7.29) с р ограничениями типа (7.28). Доказано, что решение этой задачи можно представить в виде

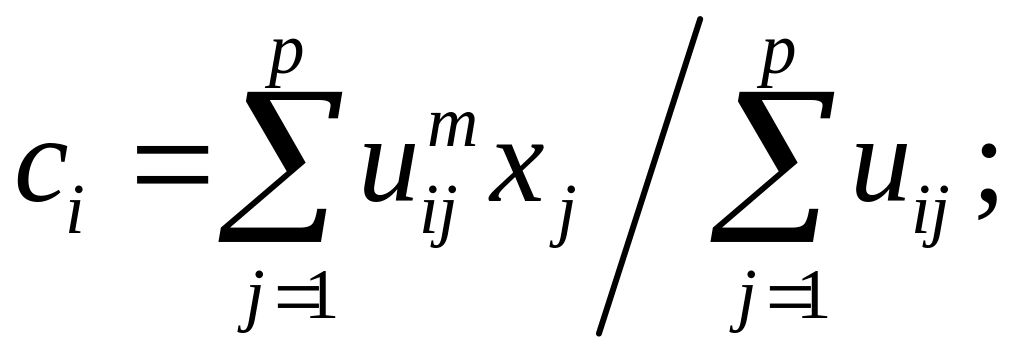(7.30)

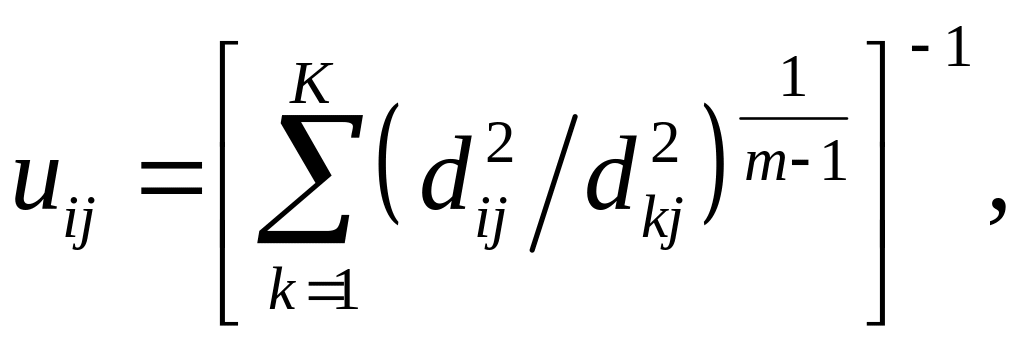(7.31)

т.е. итерационный процесс алгоритма С–means будет выглядеть так:

1. Случайная инициализация u_ij[0,1] при выполнении условия (7.28).

2. Определение положения K центров с_i в соответствии с (7.30).

3. Расчет значения функции Е согласно (7.29) и, если оно удовлетворяет критериям останова, завершение вычислений, если нет, то переход к п.4.

4. Вычисление новых значений u_ij по формуле (7.31) и переход к п.2.

Полученное в результате итерационной процедуры значение функции E необязательно будет глобальным минимумом, ибо качество находимых центров существенным образом зависит от предварительного подбора как значений u_ij, так и с_i. Поэтому обычно расчет оптимальных значений центров предваряется их начальной инициализацией с помощью специальных алгоритмов пикового или разностного группирования входных данных, использующих в качестве меры плотности размещения векторов так называемые пиковые функции. Такой подход значительно сокращает длительность итерационного процесса при определении с_i, более того, их использование в гибридном алгоритме обучения нечеткой НС значительно сокращает вычислительные затраты и гарантирует сходимость решения к глобальному минимуму.

Заметим, что независимо от способа обучения НС с нечеткой СО выполняет группирование данных по различным центрам на основе коэффициентов принадлежности u_ij[0,1]. Если принять, что вектор с принадлежностями u_ij представляется К центрами с_i, то реконструкция исходного происходит согласно

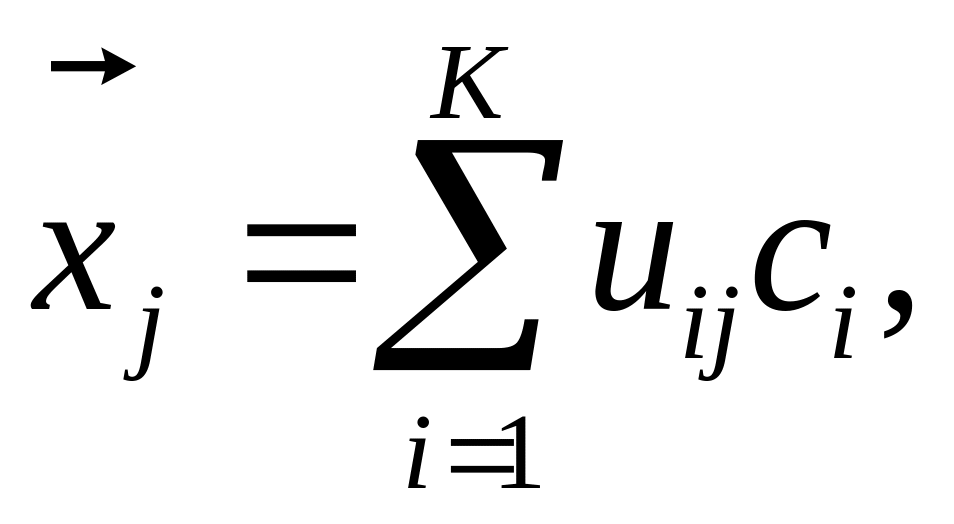(7.32)

т.е. влияние каждого центра на значение восстановленного различно и зависит от расстояния между ними, в чем и заключается основное отличие нечеткой СО от классической СО Кохонена.