- •Затверджено
- •Навчально-методичний посібник
- •5.03050801 „Фінанси і кредит”, 5.03050401 „Економіка підприємства”
- •Тема 1.1. Вступ. Множини та операції над ними
- •Тема 1.2. Комбінаторика. Біном Ньютона
- •1.1. Вступ. Множини та операції над ними Література
- •Питання, що виносяться на самостійну роботу:
- •Перехід від алгебраїчної форми запису комплексного числа до тригонометричної, показникової і навпаки
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Розв’язування квадратних рівнянь з від’ємним дискримінантом
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •1.2. Комбіноторика. Біном Ньютона Література
- •Питання, що виносяться на самостійну роботу:
- •Основні принципи комбінаторики
- •Розв’язування комбінаторних задач
- •Тема 2.1. Матриці та визначники
- •Тема 2.2. Системи лінійних алгебраїчних рівнянь
- •2.1. Матриці та визначники Література
- •Питання, що виносяться на самостійну роботу:
- •Розв’язування матричних рівнянь
- •Розв’язування матричних рівнянь:
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Знаходження рангу матриць з використанням елементарних перетворень
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Тема 3.1. Векторна алгебра
- •Тема 3.2. Аналітична геометрія
- •3.1. Векторна алгебра Література
- •Питання, що виносяться на самостійну роботу:
- •Векторні та скалярні величини. Координати вектора. Дії над векторами в координатній формі. Скалярний добуток і його властивості. Кут між векторами
- •Координати вектора
- •Дії над векторами в координатній формі
- •Розв’язання
- •Приклади для самостійного розв’язування
- •3.2. Аналітична геометрія Література
- •Питання, що виносяться на самостійну роботу:
- •Розв’язування задач на криві другого порядку
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Тема 4.1. Задачі лінійного програмування
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Тема 5.1. Функціональна залежність. Елементарні функції. Границя функції. Неперервність функції
- •5.1 Функціональна залежність. Елементарні функції. Границя функції. Неперервність функції Література
- •Питання, що виносяться на самостійну роботу:
- •Означення функціональної залежності. Функції в економіці. Способи задання функцій
- •Розв’язання
- •Способи задання функції:
- •За означенням, для взаємно обернених функцій маємо:
- •Приклади для самостійного розв’язування
- •Дослідження основних властивостей функції: області визначення, парності, непарності функції, періодичності за аналітичним заданням функції
- •Розв’язання
- •Елементарні функції
- •Приклади для самостійного розв’язування
- •Тема 6.1. Похідна функції та диференціал
- •Тема 6.2. Застосування диференціального числення до дослідження функцій та побудови їх графіків
- •6.1. Похідна функції та диференціал Література
- •Питання, що виносяться на самостійну роботу:
- •Задачі, які приводять до поняття похідної. Геометричний та механічний зміст похідної. Означення похідної функції. Основні правила диференціювання
- •Властивості еластичності функції:
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Означення похідної функції
- •Механічний зміст похідної:
- •Основні правила диференціювання
- •Доведення
- •Похідні функцій заданих неявно та параметрично
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Диференціал, його геометричний зміст. Застосування диференціала до наближених обчислень.
- •Диференціали вищих порядків
- •Питання, що виносяться на самостійну роботу:
- •Зростання, спадання та екстремуми функцій, необхідні та достатні умови. Асимптоти до графіка функцій Зростання та спадання функції
- •Розв’язання
- •Доведення
- •Екстремуми функції
- •Проте виявляється, що цього недостатньо, бо може , а функція в цій точці екстремуму не має.
- •Якщо в критичній точці, то нічого конкретного сказати не можна, бо в цій точці може бути екстремум, а може й не бути.
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Асимптоти до графіка функцій
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Дослідження функцій за допомогою похідної
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Тема 7.1. Функції багатьох змінних. Екстремуми функцій багатьох змінних
- •7.1. Функції багатьох змінних. Екстремуми функцій багатьох змінних Література
- •Питання, що виносяться на самостійну роботу:
- •Границя та неперервність функцій кількох змінних
- •Розв’язання
- •Доведення
- •Неперервність функцій двох змінних
- •Неперервність складеної (складної) функції двох змінних
- •Приклади для самостійного розв’язування
- •Найбільше та найменше значення функції в замкненій області
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Застосування диференціального числення функцій багатьох змінних до наближених обчислень
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Тема 8.1. Невизначений інтеграл
- •Тема 8.2. Визначений інтеграл та його застосування
- •Тема 8.3. Диференціальні рівняння першого порядку
- •8.1. Невизначений інтеграл Література
- •Питання, що виносяться на самостійну роботу:
- •Первісна функція. Невизначений інтеграл і його властивості. Таблиця невизначених інтегралів
- •І. Похідна від невизначеного інтеграла дорівнює підінтегральній функції
- •Метод інтегрування частинами
- •Приклади для самостійного розв’язування
- •8.2. Визначений інтеграл та його застосування Література
- •Питання, що виносяться на самостійну роботу:
- •Визначений інтеграл та його основні властивості
- •Приклади для самостійного розв’язування
- •Обчислення довжини дуги плоскої фігури, об’єму тіла обертання Площа фігури
- •Розв’язання
- •Область задана в полярних координатах
- •Об’єм тіла, отриманого при обертанні кривої навколо координатної вісі
- •Розв’язання
- •Питання, що виносяться на самостійну роботу:
- •Розв’язування вправ на диференціальні рівняння першого порядку
- •Розв’язання
- •Рівняння з відокремлювальними змінними
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Лінійні рівняння
- •Розв’язання
- •Розв’язання
- •Однорідні рівняння
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Тема 9.1. Числові ряди, їх збіжність.
- •Тема 9.2. Степеневі ряди.
- •9.1. Числові ряди, їх збіжність Література
- •Питання, що виносяться на самостійну роботу:
- •Ряд геометричної прогресії, його збіжність
- •Розв’язання
- •Радикальна ознака Коші. Використання ознак збіжності рядів з додатними членами
- •Візьмемо другий додатний числовий ряд, збіжність чи розбіжність якого відома
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язування
- •Знакопочергові ряди. Ознака Лейбніца
- •Розв’язання
- •Приклади для самостійного розв’язування
- •9.2. Степеневі ряди Література
- •Питання, що виносяться на самостійну роботу:
- •Ряди Тейлора та Маклорена. Розклад елементарних функцій в ряд Маклорена.
- •Приклади для самостійного розв’язування
Приклади для самостійного розв’язування
Обчислити інтеграли:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]()
Обчислення довжини дуги плоскої фігури, об’єму тіла обертання Площа фігури
Декартові координати. Попередньо ми вже сформували геометричний зміст визначеного інтегралу: якщо f(x)>0 на відрізку [a,b], то дорівнює площі криволінійної трапеціїи ABCD, що обмежена знизу відрізком [a,b], зліва та справа - прямими x = a і x = b, зверху - функцією y = f(x).
Наслідок: якщо фігура обмежена зверху кривою y = f(x), знизу – кривою y = g(x), зліва та справа – відрізками прямих x = a і x = b, то її площа дорівнює:
![]()
Приклад. Знайти площу області D, що обмежена кривими y = x2 + x + 11, y = 2x - 9, при умові, що х ≤ 1.
Розв’язання
Н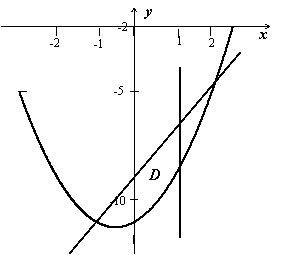 адалі
ми будемо записувати так:
адалі
ми будемо записувати так:
![]()
При розв’язуванні подібних задач слід обов’язково зобразити досліджуваний геометричний об’єкт.
Для визначення нижньої межі інтегрування необхідно знайти точку перетину кривих; рівняння x2 + x + 11 = 2 x - 9 має два корені: x = -1 та x = 2. Вірний корінь - x = -1. Область обмежена зверху параболою, знизу – прямою, справа – прямою x = 1, крайня ліва точка - x = -1, тому:
![]()
Відповідь. S (D) = 10/3.
Якщо область має більш складну структуру, її слід розбити на прості частини.
Область задана в полярних координатах
Якщо область D - сектор, обмежений променями φ = α, φ = β та кривою r = r(φ), формула для знаходження площі отримується з допомогою слідуючої інтегральної конструкції.
Розіб’ємо
проміжок α
≤ φ ≤ β
променями α
= φ0
<
φ1
<…< φі-1
< φі
<…< φn
< β
на n
частин;
![]() .
На кожному з відрізків
.
На кожному з відрізків
![]() виберемо довільну точку ξі,
знайдемо r(ξі),
тоді
виберемо довільну точку ξі,
знайдемо r(ξі),
тоді
![]() дорівнює площі сектора круга, обмеженого
променями
дорівнює площі сектора круга, обмеженого
променями
![]() ,
,
![]() та дугою кола радіуса r(ξі).
Об’єднання цих секторів – знову
ступінчаста фігура, наближуючи дану
область D,
її
площа:
та дугою кола радіуса r(ξі).
Об’єднання цих секторів – знову
ступінчаста фігура, наближуючи дану
область D,
її
площа:
![]()
При
![]() різниця
між Sступ
та
S
- площею
області
D
– буде
також наближатися до нуля, так як:
різниця
між Sступ
та
S
- площею
області
D
– буде
також наближатися до нуля, так як:
![]() .
.
Приклад.
Знайти
площу, обмежену лемніскатою
![]() .
.
Розв’язання
Точки
лемніскати
розміщені в секторах
![]() та
та
![]() ;
крім
того, при розв’язуванні таких задач
доцільно використовувати симетрію
фігури, тому ми знайдемо площу частини,
розміщеної в секторі
;
крім
того, при розв’язуванні таких задач
доцільно використовувати симетрію
фігури, тому ми знайдемо площу частини,
розміщеної в секторі
![]() і
збільшимо її вчетверо:
і
збільшимо її вчетверо:
![]() .
Відповідь.
S
= 2a2.
.
Відповідь.
S
= 2a2.
Приклад.
Знайти
площу, що знаходиться всередині кардиноїди
![]() поза
колом
поза
колом
![]() .
.
Р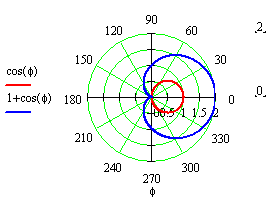 озв’язання
озв’язання
Знайдемо
різницю площ областей, що знаходяться
всередині кардиноїди та кола. Для
верхньої частини кардиноїди
![]() ;
для верхньої
частини кола
,
тому:
;
для верхньої
частини кола
,
тому:
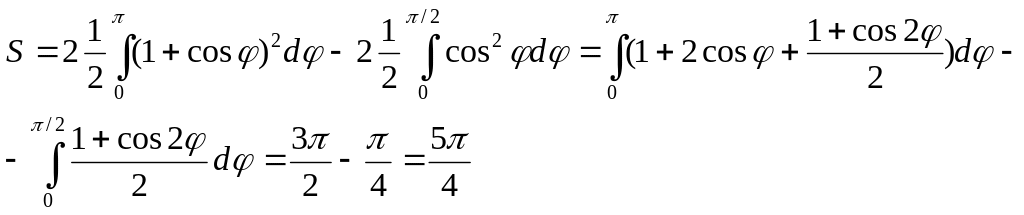
Відповідь. S = 5π/4.
Приклад.
Знайти
площу, що лежить всередині кола
![]() поза
лемніскатою
поза
лемніскатою
![]() .
.
Р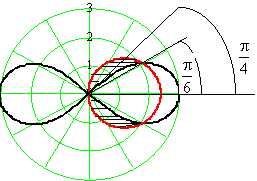 озв’язання
озв’язання
Точки перетину лемніскати та кола знаходимо з умови:
![]() ,
,
![]()
Область симетрична відносно полярної осі, тому знаходимо площу верхньої частини та подвоюємо її.
При
зміні φ
від
![]() до
до
![]() полярний радіус змінюється від
полярний радіус змінюється від
![]() до
до
![]() ;
при зміні
φ
від
до
;
при зміні
φ
від
до
![]() полярний радіус змінюється від 0
до
;
тому:
полярний радіус змінюється від 0
до
;
тому:
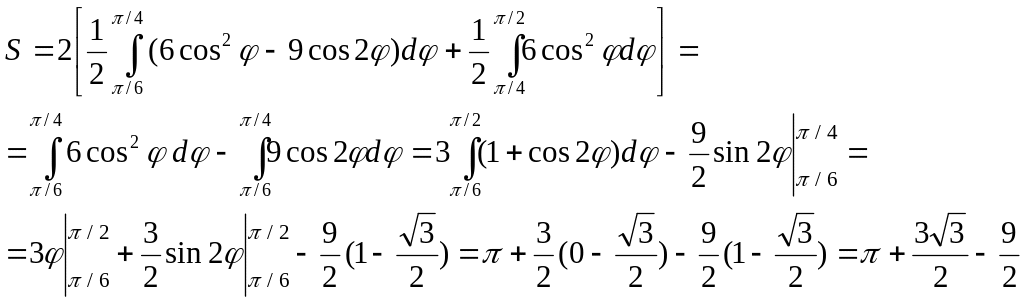
Відповідь.
S
=
![]()
Область обмежена кривими, заданими параметрично
Якщо
крива, що обмежую криволінійну трапецію
ABCD
задана в параметричному
вигляді:
![]()
![]() ,
а
= φ(t0),
b
= φ(tk);
то перехід
в інтегралі
,
а
= φ(t0),
b
= φ(tk);
то перехід
в інтегралі
![]() до
змінної t
призводить
до формули:
до
змінної t
призводить
до формули:
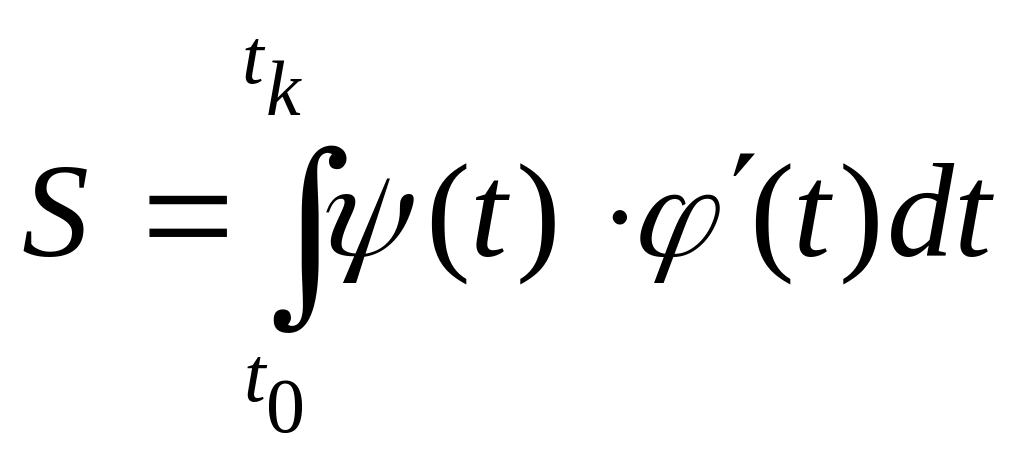
Приклад.
Знайти площу, обмежену астроїдою
![]()
![]() .
.
Розв’язання
Використаємо
симетрію фігури. Знаходимо площу частини
фігури, що розміщена в першому квадранті
(![]() ),
та
збільшимо її в 4
рази. Точку
(0, a)
отримуємо
при
),
та
збільшимо її в 4
рази. Точку
(0, a)
отримуємо
при
![]() ,
точку
(a,
0) - при t
= 0, тому:
,
точку
(a,
0) - при t
= 0, тому:
![]()
Відповідь.
![]()
Обчислення довжини кривої
Н ехай
на площині задана крива AB.
Розіб’ємо
дану криву
точками A
= M0,
M1,
M2,
…, Mi-1,
Mi,
…, Mn
= B
на n
частин
і впишемо в криву ламану
M0
M1
M2
…Mi-1
Mi
… Mn,
яка
з’єднує ці точки.
Довжина
L
лам
цієї
ламаної дорівнює сумі довжин прямолінійних
ланок, з’єднуючих точки розбиття:
ехай
на площині задана крива AB.
Розіб’ємо
дану криву
точками A
= M0,
M1,
M2,
…, Mi-1,
Mi,
…, Mn
= B
на n
частин
і впишемо в криву ламану
M0
M1
M2
…Mi-1
Mi
… Mn,
яка
з’єднує ці точки.
Довжина
L
лам
цієї
ламаної дорівнює сумі довжин прямолінійних
ланок, з’єднуючих точки розбиття:
![]()
Спрямуємо
тепер кількість
n
точок
розбиття до нескінченності так, щоб
максимальна
довжина ланки
![]() прямувала
до нуля.
Якщо
при цьому існує кінцева границя
послідовності довжин ламаних
L
лам,
не залежних
від способу розбиття кривої, то крива
називається
спрямленою,
а значення
цієї границі називається довжиною
кривої AB.
прямувала
до нуля.
Якщо
при цьому існує кінцева границя
послідовності довжин ламаних
L
лам,
не залежних
від способу розбиття кривої, то крива
називається
спрямленою,
а значення
цієї границі називається довжиною
кривої AB.
Довжина кривої в декартових координатах. Нехай тепер крива AB - графік функції кривої y = f(x), що має неперервну похідну f '(x), а ≤ х ≤ b. Тоді точка Mi має координати (xi, f(xi)), ланка Mi-1Mi має довжину:
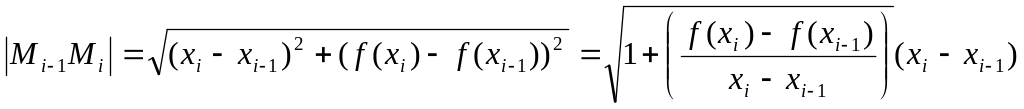 .
.
Функція
y =
f(x)
на відрізку
[xi-1,
xi]
задовольняє
умовам теореми
Лагранжа, тому існує
точка
![]() [xi-1,
xi]
така, що
[xi-1,
xi]
така, що
![]() .
Враховуючи
те, що довжина ланки Mi-1Mi
дорівнює
.
Враховуючи
те, що довжина ланки Mi-1Mi
дорівнює
![]() ,
довжина
всієї ламаної -
,
довжина
всієї ламаної -
![]() .
Остання
сума – інтегральна сума для інтегралу
.
Остання
сума – інтегральна сума для інтегралу
![]() ,
і,
внаслідок
неперервності підінтегральної функції,
прямує до нього при
,
і,
внаслідок
неперервності підінтегральної функції,
прямує до нього при
![]() .
Отже,
довжина
кривої, що задана декартовим рівнянням
y =
f(x),
а ≤ х ≤ b,
визначається
за формулою:
.
Отже,
довжина
кривої, що задана декартовим рівнянням
y =
f(x),
а ≤ х ≤ b,
визначається
за формулою:
Приклад. Знайти довжину відрізка параболи y = x2 від точки A(0,0) до точки B(2,4).
Розв’язання
![]() ,
,
![]() ,
тому:
,
тому:
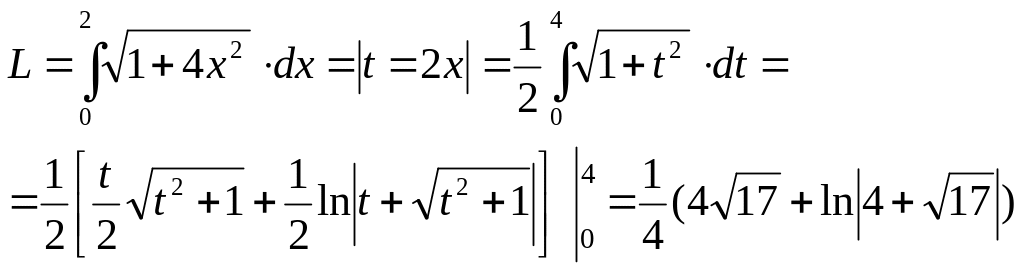
Відповідь.
![]()
Довжина кривої, що задана параметрично
![]() ,
а
= φ(t0),
b
= φ(tk);
,
а
= φ(t0),
b
= φ(tk);
Замінимо
в
змінну x
на змінну
t.
Так як
![]() ,
то
,
то
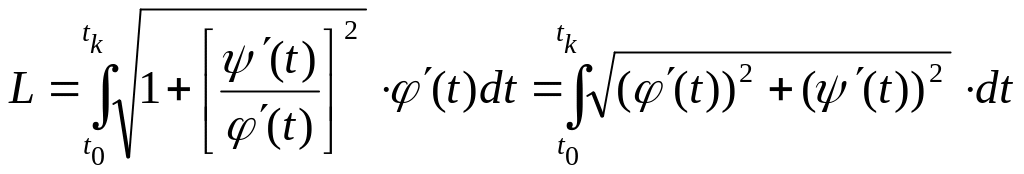 .
.
Отже, довжина кривої, що задана параметрично, визначається за формулою:
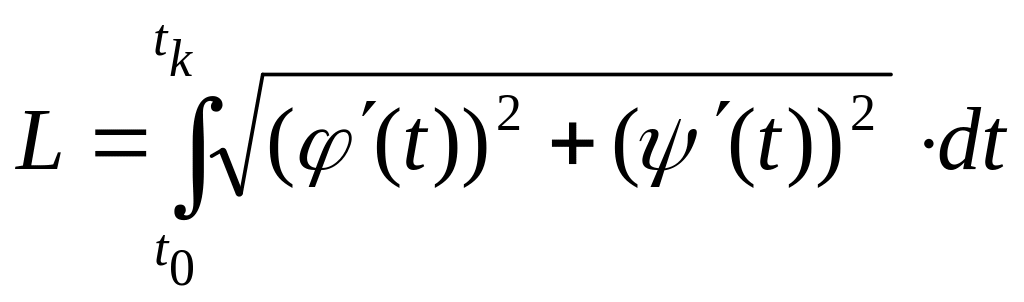
Приклад. Знайти ділянки розкладки кола, що відповідає одному завитку нитки.
Розв’язання
Крива задається рівняннями:
![]()
![]()
Відповідь.
![]()
Крива
задана в полярних
координатах.
Випадок,
коли крива
задається
рівнянням r
= r(φ),
α ≤ φ ≤ β,
легко зводиться
до попереднього.
Так як
![]() ,
,
![]() ,
то, розглядаючи
полярний кут φ
як параметр, отримаємо:
,
то, розглядаючи
полярний кут φ
як параметр, отримаємо:
![]() ,
тому:
,
тому: ![]()
Приклад.
Знайти
довжину
кардиноїди
![]() .
.
Розв’язання
![]() ,
тому:
,
тому:
![]() .
Відповідь
явно безглузда. Де ж помилка? Помилка в
тому, що не врахований знак модуля при
добуванні кореня з
.
Відповідь
явно безглузда. Де ж помилка? Помилка в
тому, що не врахований знак модуля при
добуванні кореня з
![]() .
.
Правильний розв’язок:

Проте, як і в попередніх випадках, простіше користуватися симетрією фігури, знайти довжину верхньої вітки та подвоїти її:
![]()
Відповідь. L = 8a.
Об’єми тіл обертання

Обчислення
об’єму за площами поперечних перерізів.
Нехай
тіло V
розміщено
в просторі між площинами x
= a
і x
= b,
і для
![]() відома площа його поперечного перерізу
S
= S(x).
Необхідно знайти об’єм цього тіла.
Розріжемо
це тіло площинами x
= x0
= a,
x
= x1,
x
= x
2, …, x
= xi-1,
x
= xi,
…, x
= x
n-1,
x
= xn
= b
на n
шарів
(a =
x0<
x1
< < x2<
…< xn-1
< xn
= b),
на кодному
з відрізків [xi-1,
xi]
візьмемо
довільну точку ξі;
вважатимемо, що об’єм
шару, що знаходиться між площинами x
= xi-1
та
x
= xi
приблизно
дорівнює об’єму
відома площа його поперечного перерізу
S
= S(x).
Необхідно знайти об’єм цього тіла.
Розріжемо
це тіло площинами x
= x0
= a,
x
= x1,
x
= x
2, …, x
= xi-1,
x
= xi,
…, x
= x
n-1,
x
= xn
= b
на n
шарів
(a =
x0<
x1
< < x2<
…< xn-1
< xn
= b),
на кодному
з відрізків [xi-1,
xi]
візьмемо
довільну точку ξі;
вважатимемо, що об’єм
шару, що знаходиться між площинами x
= xi-1
та
x
= xi
приблизно
дорівнює об’єму![]() циліндра
з площею основи S(ξі)
та
висотою
циліндра
з площею основи S(ξі)
та
висотою
![]() :
:
![]() .
Сума
об’ємів
- об’єм
ступінчатої фігури, при
.
Сума
об’ємів
- об’єм
ступінчатої фігури, при![]() наближається
до шуканого об’єму V,
тому:
наближається
до шуканого об’єму V,
тому:
![]()