
Глухов Ю.П. Конспект
лекций по высшей математике. Лекция
№ 36
Лекция 36 тема: Дифференциальные уравнения. Однородные уравнения
План.
Однородные уравнения.
Подстановка Бернулли.
Метод Лагранжа
Уравнение в полных дифференциалах
Особые точки и особые решения.
1. Однородные уравнения
Определение. Функция f(x,y) называется однородной функцией n-порядка относительно переменных x и y, если при любом t выполняется тождество
![]()
Пример.
![]() -однородная функция
первого порядка, т.к.
-однородная функция
первого порядка, т.к.
![]()
Пример.
![]() -однородная
функция второго порядка,
т.к.
-однородная
функция второго порядка,
т.к.
![]()
Пример.
![]() -однородная
функция нулевого порядка,
т.к.
-однородная
функция нулевого порядка,
т.к.
![]()
К уравнениям с разделяющимися переменными приводятся и так называемые однородные дифференциальные уравнения первого порядка, имеющие вид:
![]() . (31.1)
. (31.1)
Действительно, замена
![]() или y = xt
приводит к
или y = xt
приводит к
![]()
![]()
![]()
![]()
![]()
Еще одной формой однородного уравнения является уравнение
M(x,y) dx + N(x,y) dy = 0, (31.2)
если М(х,у) и N(x,y)
– однородные функции одинаковой степени
однородности. При этом
![]() .
.
Пример
y² + x²y′ = xyy′.
Решение.
Преобразуем уравнение к виду (31.1):
y′(xy
– x²) = y²,
![]() ,
,
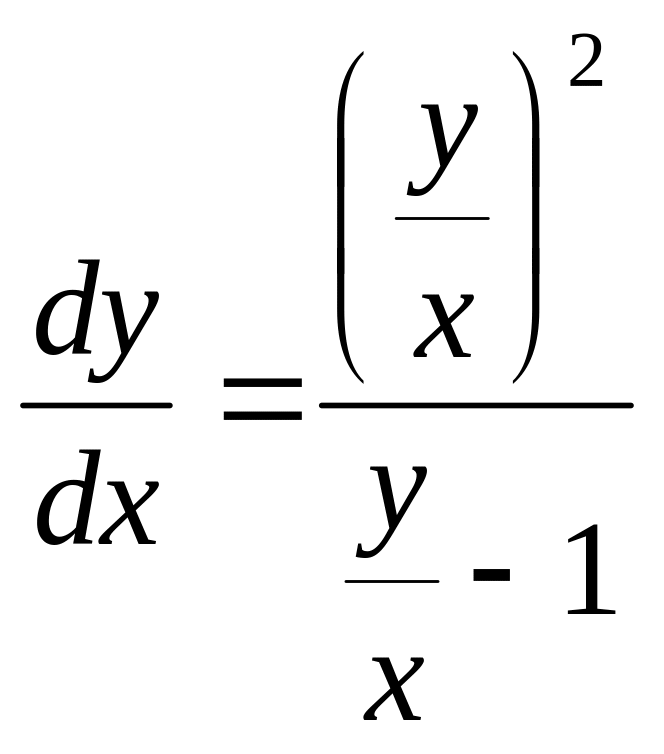 .
После замены y = xt
получим:
.
После замены y = xt
получим:
![]()
![]()
![]() ,
,
![]() t – ln
| t | = ln
| x | + ln
|C| ,
t – ln
| t | = ln
| x | + ln
|C| ,
![]() ,
,
![]() .
.
В однородные можно преобразовать и уравнения вида
![]() (31.3)
(31.3)
с помощью замены Х = х – х1 , Y = y – y1 , где х1 , у1 – решение системы уравнений
a1x + b1y + c1 = 0, a2x + b2y + c2 = 0.
(C геометрической точки
зрения производится перенос начала
координат в точку пересечения прямых
a1x
+ b1y
+ c1 = 0
и a2x
+ b2y
+ c2 = 0).
Тогда, поскольку
![]() ,
в новых переменных уравнение примет
вид:
,
в новых переменных уравнение примет
вид:
![]() или
или
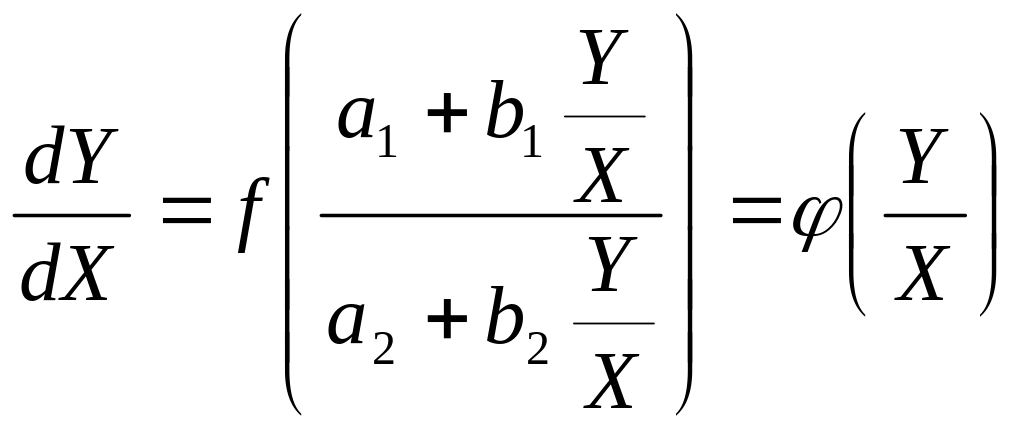 - однородное уравнение.
- однородное уравнение.
Пример
(у + 2) dx = (2x + y – 4)dy.
Решение.
Запишем уравнение в виде
![]() .
Решением системы у + 2 = 0, 2х + у –
4 = 0 будут х1 = 3, у1
= -2. В новых переменных Х = х – 3,
.
Решением системы у + 2 = 0, 2х + у –
4 = 0 будут х1 = 3, у1
= -2. В новых переменных Х = х – 3,
Y = y
+ 2 получим однородное уравнение
![]() ,
которое можно решить с помощью обычной
замены Y = Xt.
Тогда
,
которое можно решить с помощью обычной
замены Y = Xt.
Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() и после обратной замены общий интеграл
выглядит так:
и после обратной замены общий интеграл
выглядит так:
![]() .
Заметим, в это общее решение входит при
С=0 и частное решение у = 1 – х,
которое могло быть потеряно при делении
на у + х –1.
.
Заметим, в это общее решение входит при
С=0 и частное решение у = 1 – х,
которое могло быть потеряно при делении
на у + х –1.
Линейные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение вида
![]() ,
(32.1)
,
(32.1)
линейное относительно неизвестной функции у(х) и ее производной. При этом будем предполагать, что р(х) и f(x) непрерывны.
В случае, когда f(x) ≡ 0, уравнение (32.1) называется однородным. Такое уравнение является уравнением с разделяющимися переменными:
![]() ,
откуда
,
откуда
![]()
![]()
![]() .
(32.2)
.
(32.2)
При делении на у могло быть потеряно решение у = 0, но оно входит в общее решение при С = 0.
