Пример 9.
Первоначальная сумма долга равна 50 млн руб. Определить наращенную сумму долга через 2,5 года, используя способ начисления смешанных процентов по ставке 25 % годовых.
Для смешанных или комбинированных процентов имеем согласно формуле (2.12):
млн руб.
Пример 10.
31 марта 2010 г. была получена в долг сумма 40 тыс. руб. под 32 % годовых. Долг был возвращен 11 июня 2013 г. Какая сумма была возвращена?
При использовании в расчетах комбинированных процентов согласно (2.12) получается сумма:
тыс. руб.
При расчете кредитования могут возникать различные задачи. В формуле для сложных процентов (2.10) и непрерывных процентов (2,12), имеется четыре параметра. Можно задать любые три из них, а четвертый параметр определить из уравнения (2.10) или (2,12). В соответствии с этим возникают различные экономические задачи. Например, следующие.
Пример 11.
За какой срок первоначальный капитал 50 млн руб. увеличится до 200 млн руб., если:
а) на него начисляются сложные проценты по ставке 28 % годовых;
б) проценты начисляются ежеквартально;
в) проценты начисляются непрерывно?
Решение.
Согласно
(2.9) для случая «а» начальная и конечная
суммы связаны соотношением
.
Отсюда, находим время t:
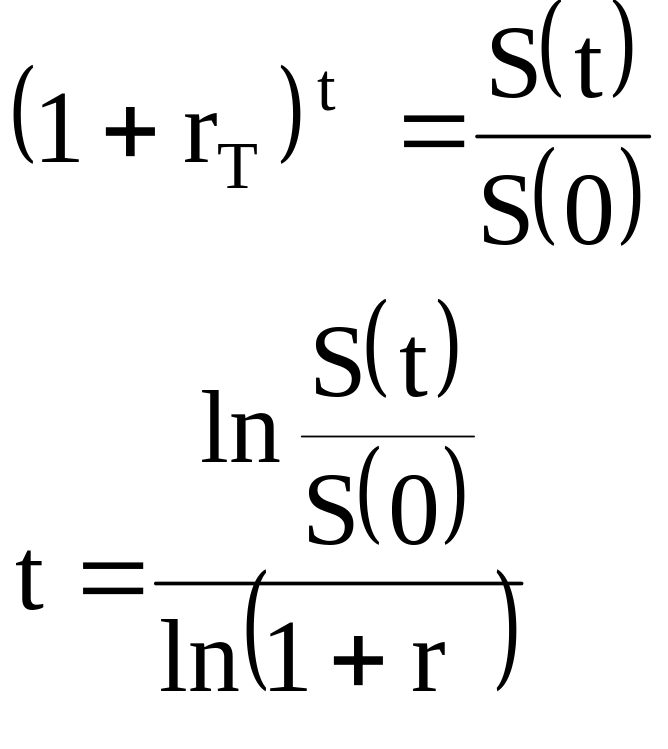
Подставляя численные значения, имеем:
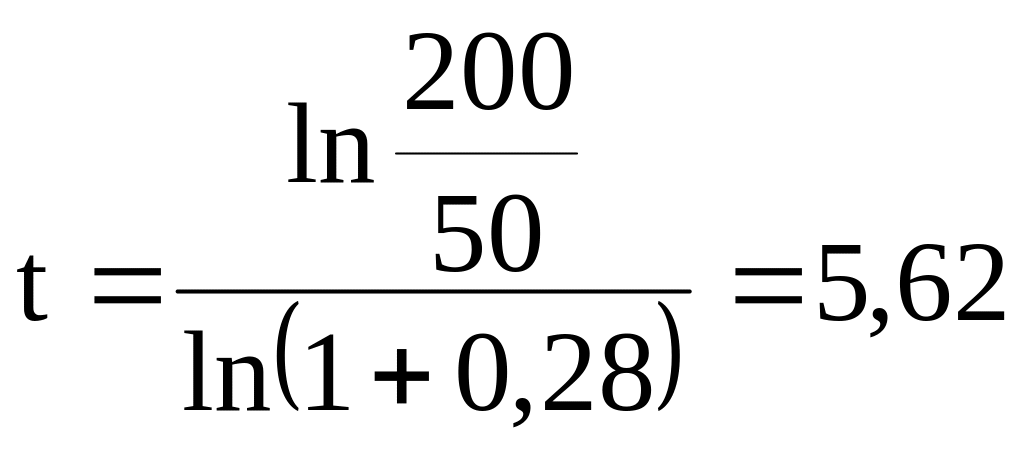года.
Аналогично,
согласно (2.11) для случая «б», когда
проценты начисляются раз m
в год, имеем уравнение для определения
длительности сделки
.
Решая уравнение, имеем:
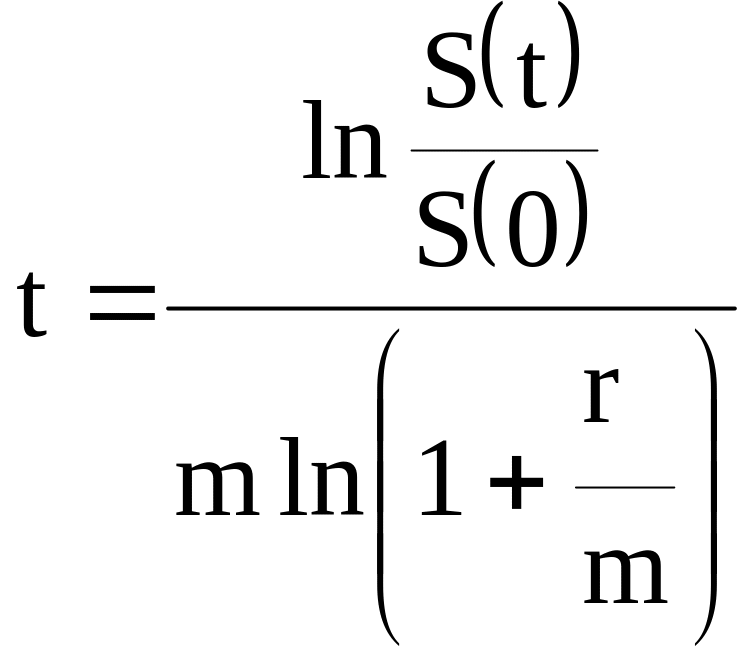. (2.14)
В нашем случае при r=0,28, m=4, S(0)=50 млн руб., S(t)=200 млн руб. для времени накопления капитала получим:
года.
Для определения периода начисления в случае «в», когда проценты начисляются непрерывно, воспользуемся формулой (2.12). Решая уравнение (2.12) относительно t получим:
(2.15)
Формула
для расчета времени (2.15) может быть
получена также из (2.14) предельным
переходом при m.
При этом нужно воспользоваться
замечательным пределом
при малых
значениях x.
Подставляя численные значения в (2.15), имеем:
t=ln(200/50)/0,28=4,95 года
Таким образом, чем чаще начисляются проценты, тем быстрее происходит накопление капитала.
Пример 12.
Если цены растут на 2 % ежемесячно, то часто за годовой уровень инфляции принимают 24 %, и банки привлекают клиентов, обещая 25 %. Каков уровень инфляции? Какую прибыль имеют клиенты банка?
Решение.
Пусть стоимость S(0) товара в начале года. Тогда, при месячном уровне инфляции r стоимость товара в конце года будет равна в соответствии с формулой сложных процентов (2.10) величине:
Приращение стоимости товара за год составит:
S(12)-S(0)=(1+r)12S(0)-S(0)=((1+r)12 - 1) S(0)
Следовательно, годовая инфляция, равная относительному повышению стоимости товара, будет иметь вид:
(2.16)
Таким образом, при месячном уровне инфляции r=2 % годовая инфляция будет составлять:
i = (1+0,02)12 - 1=26,82 %
В этом случае клиенты банка терпят убытки в размере 1,82 %.
Учитывая что, инфляция действует непрерывно каждую наносекунду, расчет годовой инфляция может быть произведен по формулам для непрерывных процентов (2.12). Действительно, в этом случае стоимость товара в конце года будет равна:
S(12)=S(0) e12 r
Приращение стоимости:
S(12)-S(0)=(e12 r-1) S(0)
Годовая инфляция (относительное повышению стоимости товара за год), будет равна:
(2.17)
или в нашем случае:
Очевидно, годовая инфляция 27,12 %, вычисленная по формулам непрерывных процентов, чуть больше годовой инфляции 26,82 %, рассчитанной по формулам сложных процентов.
Пример 13.
Банк предлагает потребительский кредит под 3 % в месяц. Какова годовая процентная ставка кредита?
Решение.
На первый взгляд кажется, что годовая процентная ставка кредита равна 3 %*12=36 %. Однако, правильное значение ставки получается с учетом формул сложных процентов. Используя рассуждения, аналогичные приведенным в примере 12, получим правильное значение процентной ставки в виде (см. формулу 2.16):
rгод=(1+r)12-1 = (1+0,03)12-1=42,58 %
Таким образом, истинное значение годовой процентной ставки потребительского кредита 42,58 % превышает предполагаемое значение 36 % на 6,8 %.
Удвоение капитала. Правило 72. В банк под r процентов годовых вложен капитал. Для клиента банка процентная ставка r является достаточно абстрактной величиной. Ему хотелось бы знать, за какой срок капитал удвоится при этой ставке?
Предположим сначала, что проценты начисляются непрерывно. Тогда, воспользовавшись формулой для непрерывных процентов (2.12), получим для времени удвоения капитала из (2.15) формулу:
,
где r%=100*r ставка в процентах.
Таким образом, в случае непрерывного начисления процентов получается точное «правило 70», т. е. время за которое капитал удвоится равно70/r %, где r выражено в процентах. Например, при r% =10 % капитал увеличится в два раза за 7 лет.
В банке проценты начисляются дискретно раз в год, раз в полгода, раз в квартал. При этом время удвоения капитала немного возрастает и в банковском деле используется полуэмпирическая формула «правило 72» в виде:
(2.18)
Правило 72: Если процентная ставка есть r%, то удвоение капитала произойдет через 72/ r %.
В таблице 1.1 приведена зависимость времени удвоения капитала от процентной ставки:
Таблица 1.1
-
r %
t годы
5 %
14,4
10 %
7,2
20 %
3,6
Дадим дополнительное обоснование цифре 72 в формуле (2.18) («правило 72»). В дискретном случае, при начислении r процентов годовых m в год в течение t лет, для накопленного капитала имеем формулу (2.11).
.
Отсюда, аналогично (2.14) для срока удвоения капитала получим:
где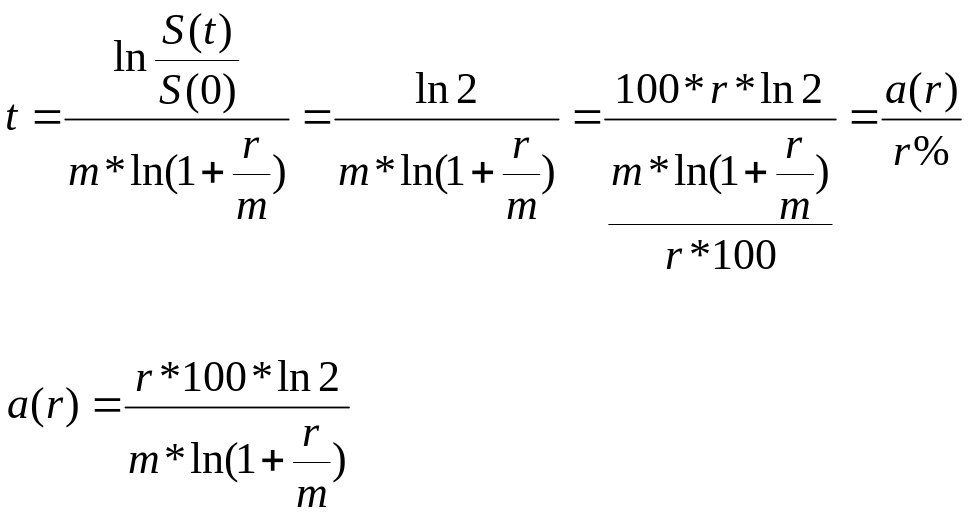
Видно, что a(r) в дискретном случае не является постоянной величиной. Она зависит от процентной ставки r и количества периодов начисления m. Однако, при малых значениях ставки r, в силу замечательного предела, ln(1+r/m) примерно равен r/m и, следовательно, a(r) приблизительно равно 70 и мало меняется. Действительно, произведем вычисления a(r) для некоторых реально встречающихся процентных ставок r и количеств периодов начисления m.
Таблица 1.2
r % |
m=4 |
m=2 |
m=1 |
a (r) |
a (r) |
a (r) |
|
8 % |
70 |
70,69 |
72,05 |
10 % |
70,17 |
71,03 |
72,72 |
12 % |
70,34 |
71,37 |
73,39 |
Из таблицы 1.2 видно, что в большинстве реальных случаев начисления процентов a(r) действительно близко к 72 и, следовательно, «правило 72» верно.
Сравнение кредитования по схеме простых и сложных процентов
Оценим выгодность для кредитора схем кредитования по простым и сложным процентам. В качестве показателя эффективности кредитования используем относительное приращение капитала:
, (2.19)
где t - период начисления, S(0) - выданная сумма, S(t) - полученная сумма.
Тогда, из (2.9) показатель эффективности для кредитования по схеме простых процентов будет равен линейной по длительности t сделки функции:
Q(t) = r t (2.20)
Показатель эффективности для кредитования по схеме сложных процентов из (2.10) будет равен показательной по t функцией:
Q(t)= (1+r) t - 1 (2.21)
При длительности сделки равной нулю (t=0), её эффективность Q(t) очевидно равна нулю. Если длительность сделки равна году (t=1), то показатели эффективности кредитования по схемам простых и сложных процентов одинаковы и равны r. Чтобы разобраться с общим случаем, построим график зависимости показателей эффективности Q(t) от длительности сделки t.
Из графика (см. рис. 2.2) видно, что при длительности сделки меньше года для кредитора более выгодна схема кредитования по простым процентам, при длительности сделки больше года для кредитора более выгодна схема кредитования по сложным процентам.
Пример 14.
Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через полгода и три года при использовании простой и сложной ставки процентов в размере 50 % годовых.
Решение.
Из (2.8) наращенная по простым процентам сумма через полгода и три года будет равна соответственно:
тыс. руб.,
тыс. руб.
Из (2.9) наращенная по сложным процентам сумма через полгода и три года будет равна соответственно:
тыс.
руб.,
тыс. руб.
Таким образом, при сроке кредитования полгода для кредитора более выгоден расчет по простым процентам. Возвращаемая сумма, рассчитанная по схеме простых процентов равна 250 тыс. руб., по схеме сложных процентов 244,949 тыс. руб. При сроке кредитования три года более выгоден расчет по сложным процентам. Возвращаемая сумма, рассчитанная по схеме простых процентов равна 500 тыс. руб., по схеме сложных процентов 675 тыс. руб.
Задача 9. Переменная ставка сложных процентов.
За время хранения вклада меняются величины процентных ставок. Пусть в периоды времени n1 , n2 … nm процентные ставки составляют r1 , r2 , rm. Найти наращенную сумму S(t), если начальный вклад равен S(0).
Ответ.
