Тема 4. Система пар сил

а) Параллельные силы направлены в одну сторону

Рассмотрим твердое тело, на которое действуют две параллельные силы и, приложенные в точкахитела (рис.20,а). Требуется определить модуль и точку приложения равнодействующей этих двух сил.

Пользуясь аксиомами 1 и 2 статики, перейдем от данной системы параллельных сил к эквивалентной системе сходящихся сил и. Для этого приложим в точкахипрямопротивоположные силыи, направленные вдоль прямой, и сложим силы,и,по аксиоме 3 (рис. 20,б).

18

П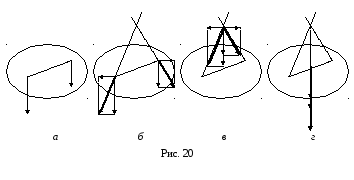олученные в результате такого сложения силыи, переносим вдоль линий их действия в точкуи раскладываем обратно на составляющие,и,. Прямопротивоположные силыиможно отбросить, при этом состояние тела не изменится (рис. 20,в).

В результате в точке получаем две силыи, направленные вдоль одной прямой. Перенесем эти силы вдоль линии их действия в точкуи находим их равнодействующую, модуль которой равен(рис. 20,г). Для определения точки приложения силы (точки) рассмотрим подобные треугольники(рис. 20,в).

,или, учитывая, что,.,

, получаем . (6)

Таким образом, равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону, равна по модулю сумме модулей слагаемых сил, им параллельна и направлена в ту же сторону. Линия действия равнодействующей проходит между точками

приложения слагаемых сил на расстояниях от этих точек, обратно пропорциональных силам.

б) Антипараллельные силы

Докажем теорему: равнодействующая двух антипараллельных сил параллельна этим силам и направлена в сторону большей из них. Модуль равнодействующей равен разности модулей данных сил, а линия действия равнодействующей делит расстояния между точками приложения данных сил внешним образом на части, обратнопропорциональные этим силам.

19

Рассмотрим твердое тело, на которое действуют две антипараллельные силы и, приложенные в точкахитела, и при этом(рис.21,а). Требуется определить модуль и точку приложения равнодействующей этих двух сил. Заменим силу двумя эквивалентными силами, приложенной в точке, причеми силой, приложенной в точке.,и, учитывая, что,,, отсюда. Это равенство определяет положение точки.

П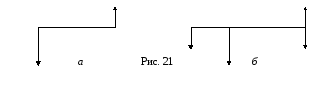реобразуем равенство,,,. Из последней полученной зависимости видно, что в этом случае линия действия равнодействующейпроходит через точку, лежащую вне отрезка, и притомближе к большей силе (рис. 21,б).

Рассмотрим частный случай, когда две антипараллельные силы равны по модулю (рис. 22,а). Такая система называется парой сил.

Ранее получили ,. В данном случае,,, т.е. равнодействующая обращается в ноль, а точка ее приложения удаляется в бесконечность. Этот результат указывает на то, что в действительностипару сил невозможно заменить одной силой, ей эквивалентной, т.е. пара не имеет равнодействующей и под действием пары сил тело может совершать только вращательное движение.

20

На практике понятие пары сил мы применяем постоянно: поворачивая вентиль крана, чтобы потекла вода, вращая рулевое колесо автомобиля и т.д. (рис. 22,б). Так как под действием пары сил тело может совершать только вращательное движение, то действие пары характеризуется ее моментом. Алгебраическим моментом пары называется взятое со знаком плюс или минус произведение одной из сил пары на плечо пары (рис. 22,а): , здесь- плечо пары, т.е. кратчайшее расстояние между линиями действия сили. Знак у момента пары определяется по тому же правилу, что и у момента силы относительно точки. Теорема о сумме алгебраических моментов сил пары.Алгебраическая сумма моментов сил пары относительного любого центра, лежащего в плоскости действия пары, не зависит от выбора этого центра и равна моменту пары.

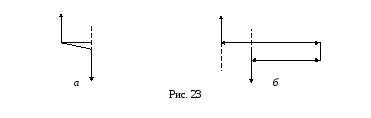
Доказательство: рассмотрим пару сил (рис. 23,а), лежащую в плоскости листа, и покажем, что сумма моментов, которую создают эти силы относительно любого центра, лежащего в плоскости листа, есть величина постоянная и равная моменту данной пары. Сначала определим момент данной

пары , а затем выбираем произвольный центр(рис. 23,б) и определяем относительно него моменты сил и:,. Тогда, так как.

Эквивалентность пар

Теорема. Две пары, лежащие в одной плоскости и имеющие численно

равные моменты и одинаковые направления вращения, эквивалентны.

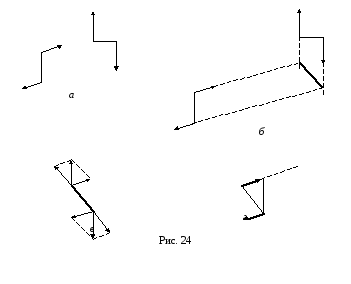
Доказательство: даны две пары и, лежащие в одной плоскости и имеющие численно равные моменты и одинаковые направления вращения(рис. 24,а). Требуется доказать, что эти пары эквивалентны.

21

Продлеваем линии действия этих сил и получаем линию пересечения плоскостей пари(рис. 24,б). Далее, переносим силы ивдоль линий их действия в точкиисоответственно и раскладываем силы на составляющие:наи, анаи(рис. 24,в). Причем ,и линии действия силинаправлены вдольисоответственно, а силыиравные прямопротивоположные и направлены вдоль. На основании аксиомы 2 , не изменяя состояния тела, силыиможно отбросить, и в результате мы получаем пару сил с плечом(рис. 24,г).

Покажем, что момент полученной пары будет численно равен моменту первоначальной пары. Для этого воспользуемся теоремой Вариньона, которая для нашего случая будет иметь вид (рис. 24,в) , причем, так как линия действия силыпересекает точку . Следовательно, или.

22

Тогда, учитывая , получаем. Учитывая, что у париодинаковые плечи и алгебраические моменты, получаем, что силы этих пар равны как по модулю, так и по направлению, т.е. данные пары эквивалентны.

Из доказанной теоремы получаем следующие следствия.

Следствие 1. Данную пару, не изменяя ее действия на тело, можно как угодно переносить в ее плоскости действия. Следовательно, действие пары на тело не зависит от ее положения в своей плоскости.

Следствие 2. Не изменяя действия данной пары на тело, можно менять модули сил и плечо данной пары, но при условии, что ее момент и направление вращения остаются неизменными.

Следствие 3. Две данные пары всегда можно привести к одному плечу.