
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
2.Производная
Пусть
![]() определена в окрестности
определена в окрестности![]() точки
точки
![]() .
.
Поскольку
на множестве
![]() определена
функция
определена
функция
![]() и
и![]() - предельная точка для
- предельная точка для
![]() ,
то
можно ставить вопрос
,
то
можно ставить вопрос
о
существовании предела разностного
отношения
![]() в точке
в точке![]() .
.
Определение
19.2.
Число
![]() (если оно существует) называютпроизводной
функции
(если оно существует) называютпроизводной
функции
![]() в точке
в точке![]() и обозначают символом
и обозначают символом![]() .
.
Итак,
![]() , (2)
, (2)
при условии, что предел существует.
Для
обозначения производной также используется
символ
![]() .
.
Например,
скорость прямолинейного движения
есть производная перемещения как функции
времени. Часто
полезно, по аналогии с этим, трактовать
и производную
любой функции
![]() в
точке
в
точке
![]() как
скорость
изменения функции в этой точке. Пример-
скорость химической реакции.
как
скорость
изменения функции в этой точке. Пример-
скорость химической реакции.
Пример
1'. Линейная
функция
![]() имеет
производную в каждой точке,
и
ее
производная
имеет
производную в каждой точке,
и
ее
производная
![]() -
постоянная.
-
постоянная.
◄Действительно,
![]() .►
.►
В частности, постоянная имеет всюду производную, равную нулю, а тождественная функция - производную, равную единице.
Пример
2'. Квадратичная
функция
![]() имеет производную в каждой точке, и ее
производная равна
имеет производную в каждой точке, и ее
производная равна![]() .
.
◄Действительно,
![]() .►
.►
Пример
3'.
Модуль
![]() не
имеет производной в точке 0.
не
имеет производной в точке 0.
◄Действительно,
![]() не существует, поскольку предел при
не существует, поскольку предел при![]() этого
отношения равен 1, а предел при
этого
отношения равен 1, а предел при![]() равен
-1 и, следовательно, предел при
равен
-1 и, следовательно, предел при![]() не существует ►
не существует ►
В
этом примере мы встретились с ситуацией,
когда существуют
![]() и
и
![]() .
Эти величины называются, соответственно,
правой
и левой производной
и обозначаются
.
Эти величины называются, соответственно,
правой
и левой производной
и обозначаются
![]() .
Для существования производной, по
теореме 9.4, необходимо и достаточно,
чтобы
.
Для существования производной, по
теореме 9.4, необходимо и достаточно,
чтобы
![]() существовали
и были равны друг другу.
существовали
и были равны друг другу.
Теорема
19.2.
Функция
![]() ,
дифференцируемая в точке
,
дифференцируемая в точке![]() ,
имеет в этой точке производную, и
последняя равна коэффициенту
,
имеет в этой точке производную, и
последняя равна коэффициенту![]() в
представлении функции
в
представлении функции
![]() по формуле (1).
по формуле (1).
◄Согласно
определению 1,
![]() --
предельная
точка области определения функции
--
предельная
точка области определения функции
![]() .
В силу формулы(1),
.
В силу формулы(1),
![]() для
всех.
для
всех.
![]() .Так
как
.Так
как
![]() при
при![]() ,
то на основании формулы(2)
заключаем,
что
,
то на основании формулы(2)
заключаем,
что
![]() существует и равна
существует и равна![]() .►
.►
Из
единственности предела следует
единственность коэффициента
![]() в
формуле (1).
Теорема
19.2 показывает, что функция
в
формуле (1).
Теорема
19.2 показывает, что функция
![]() ,
дифференцируемая в точке
,
дифференцируемая в точке![]() ,
представима в виде
,
представима в виде
![]() , (3)
, (3)
где
![]() при
при![]() .
.
На
основании теоремы 19.2 утверждения
примеров 1' - 2' являются следствиями
соответствующих утверждений примеров
1-2. Вместе с тем, пример 3’ показывает,
что функция
![]() не является дифференцируемой в точке
0.
не является дифференцируемой в точке
0.
Теорема
19.3.
Функция
![]() ,
имеющая производную в точке
,
имеющая производную в точке![]() ,
дифференцируема в этой точке.
,
дифференцируема в этой точке.
◄По
условию, существует
![]() .
Следовательно,
по теореме о представлении функции,
имеющей предел в точке,
.
Следовательно,
по теореме о представлении функции,
имеющей предел в точке,
![]() , (4)
, (4)
где
и
![]() при
при![]() .
Положим
.
Положим

Тогда
также
![]() при
при![]() и по формуле (4') для всех
и по формуле (4') для всех
![]() справедлива
формула (3). Тем самым,
справедлива
формула (3). Тем самым,
![]() дифференцируема в точке
дифференцируема в точке![]() (с коэффициентом
(с коэффициентом![]() ).►
).►
Таким
образом, сказать, что числовая функция
дифференцируема в данной точке, или
что она имеет в этой точке производную,
одно и то же. Нахождение производной
функции
![]() у функции
у функции![]() называютдифференцированием
этой
функции.
называютдифференцированием
этой
функции.
3. Касательная к графику функции
Как и нахождение скорости неравномерного движения, нахождение касательной к кривой линии - одна из основных задач, решение которых привело к созданию дифференциального исчисления.
Рассмотрим частный случай задачи о касательной, когда линией служит график функции.
Определение
19.3.
Пусть числовая функция
![]() определена на невырожденном промежутке
определена на невырожденном промежутке![]() и непрерывна в его точке
и непрерывна в его точке![]() (так что расстояние
(так что расстояние![]() от
соответствующей точки
от
соответствующей точки
![]() графика
до его точки
графика
до его точки
![]() ,
,
![]() ,
стремится к нулю при
,
стремится к нулю при![]() ) .Касательной
к
графику функции
) .Касательной
к
графику функции
![]() в точке
в точке
![]() называют
такую прямую, проходящую через
называют
такую прямую, проходящую через
![]() ,
что отношение расстояния
,
что отношение расстояния
![]() от
точки
от
точки
![]() до
этой прямой к расстоянию
до
этой прямой к расстоянию
![]() от
от
![]() до
до
![]() стремится
к нулю при
стремится
к нулю при
![]() (т.е.что
(т.е.что
![]() бесконечно
мало по сравнению с
бесконечно
мало по сравнению с
![]() при
при
![]() ).
).
Суть
этого определения можно наглядно описать
следующим образом: если представить,
что точка
![]() движется
по линии к точке касания
движется
по линии к точке касания
![]() ,то,
какова бы ни была точность наблюдения,
с некоторого момента точка
,то,
какова бы ни была точность наблюдения,
с некоторого момента точка
![]() ,
будучи
еще отличной от
,
будучи
еще отличной от
![]() ,уже
неотличима от своей проекции
,уже
неотличима от своей проекции
![]() на касательную (рис. 14). Таким образом,
кривая, обладающая в точке
на касательную (рис. 14). Таким образом,
кривая, обладающая в точке
![]() касательной, почти сливается с ней
вблизи этой точки.
касательной, почти сливается с ней
вблизи этой точки.
Теорема
19.4.
Если
функция
![]() ,
определенная на промежутке, дифференцируема
в его точке
,
определенная на промежутке, дифференцируема
в его точке![]() ,
то график этой функции имеет в
соответствующей точке
,
то график этой функции имеет в
соответствующей точке
![]() касательную,
причем угловой коэффициент касательной
равен
касательную,
причем угловой коэффициент касательной
равен
![]() .
.
◄ По условию и по теореме 19.2 предыдущего пункта, представление
![]()
![]() ,
(5)
,
(5)
с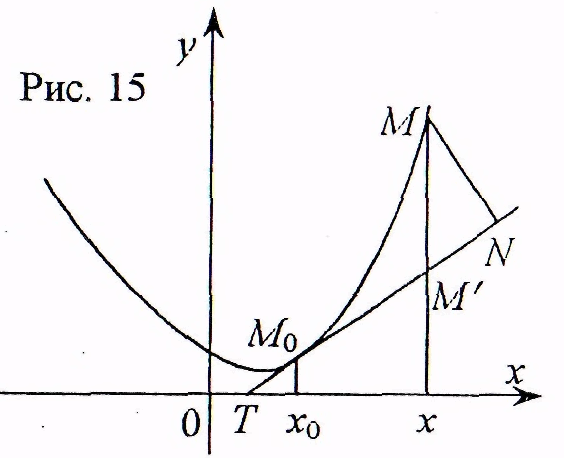 праведливо
для всех
праведливо
для всех![]() ,
принадлежащих некоторой окрестности
,
принадлежащих некоторой окрестности
![]() точки
точки
![]() ,
и
,
и![]() при
при![]() .
Прямая
с угловым коэффициентом
.
Прямая
с угловым коэффициентом
![]() ,
проходящая через точку
,
проходящая через точку
![]() ,
имеет уравнение
,
имеет уравнение
![]() .
(6)
.
(6)
Пусть
![]() - точка графика с абсциссой
- точка графика с абсциссой
![]() и
и![]() (рис. 15),
(рис. 15),
![]() -
проекция этой точки на прямую (6) и
-
проекция этой точки на прямую (6) и
![]() -точка
этой прямой с абсциссой
-точка
этой прямой с абсциссой
![]() .
Тогда
направленный отрезок
.
Тогда
направленный отрезок
![]() равен
равен
![]() ,так
что, вычитая (8) из (7), получаем
,так
что, вычитая (8) из (7), получаем
![]() .Так
как
.Так
как
![]() ,а
,а
![]() ,
то
,
то
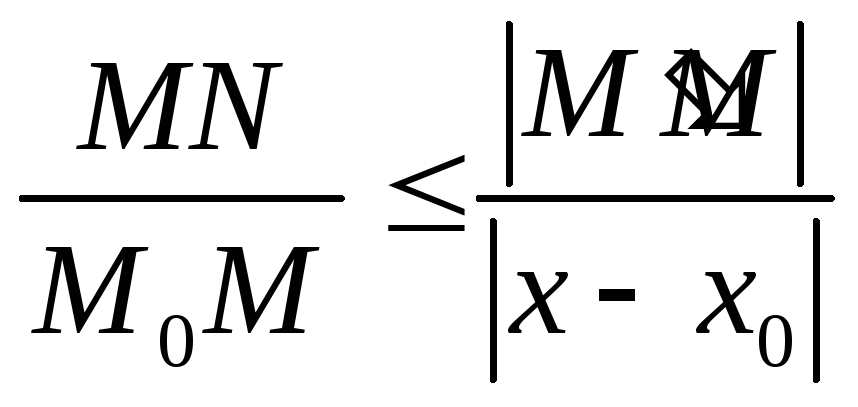 .
Но
.
Но
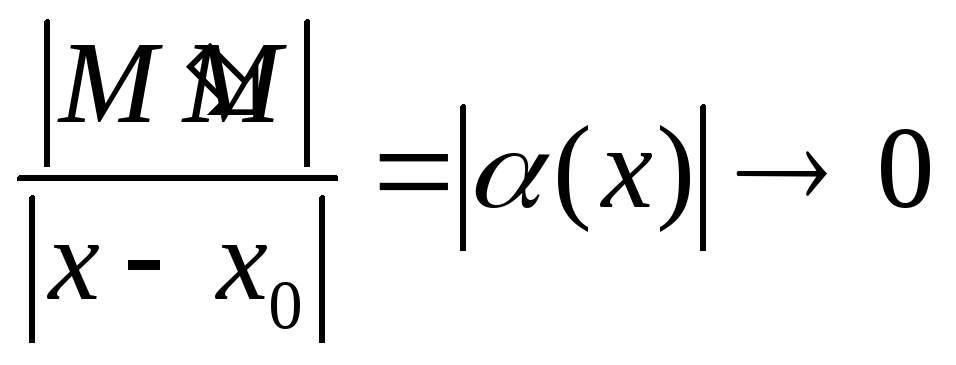 при
при
![]() .
Следовательно,
.
Следовательно,
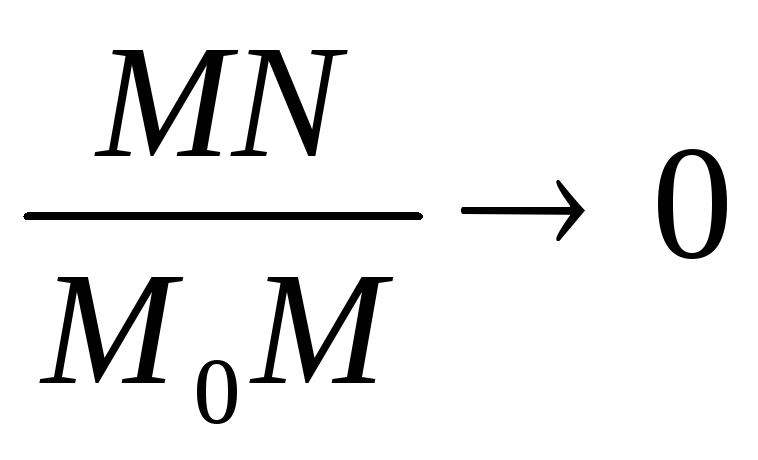 при
при
![]() ,
т.е.
(7) - уравнение касательной к графику
функции
,
т.е.
(7) - уравнение касательной к графику
функции![]() в
его точке
в
его точке
![]() .
►
.
►
Таким образом, нахождение углового коэффициента касательной (как и нахождение скорости) приводит к вычислению производной.
Замечание
1.
Секущая
![]() имеет
угловой коэффициент
имеет
угловой коэффициент (см. рис. 15). Таким образом теорема 1
показывает, что угловой
коэффициент касательной в точке
(см. рис. 15). Таким образом теорема 1
показывает, что угловой
коэффициент касательной в точке
![]() есть предел углового коэффициента
секущей
есть предел углового коэффициента
секущей![]() при
при
![]() .
.
