Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.

Пусть - функции, задающие некоторое отображение из в . Предположим, что эти функции имеют частные производные по всем переменным в некоторой точке . Тогда матрица

Называется матрицей Якоби. В случае , т. е., когда рассматривается функция , то матрица Якоби состоит из одного элемента . Поэтому эту матрицу можно считать обобщением понятия производной. Как уже отмечалось, для дифференциала отображения, соответствующего приращению , имеем

.

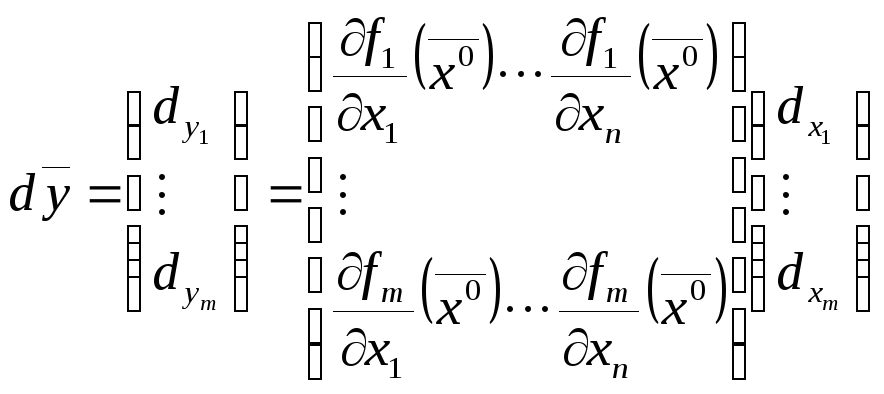Предположим, что и что, в свою очередь, Это приводит к сложному отображению (или композиции отображений) , где использованы краткие записи , , , , .

Для этого отображения, по теореме о производной сложной функции, , поэтому имеет место равенство: .

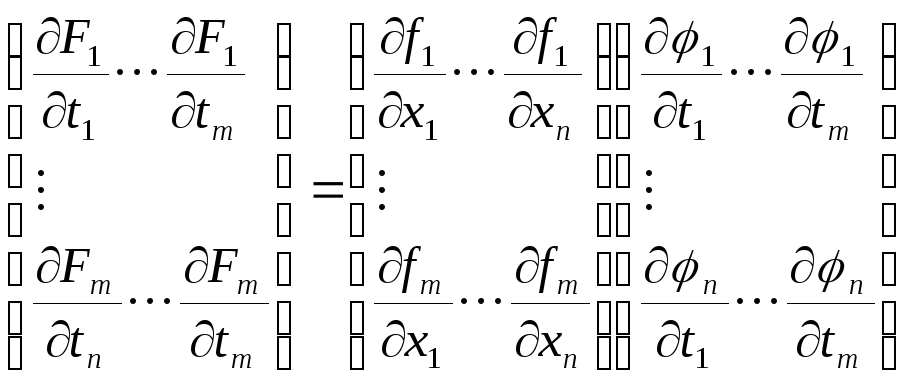В случае, когда , определитель матрицы Якоби

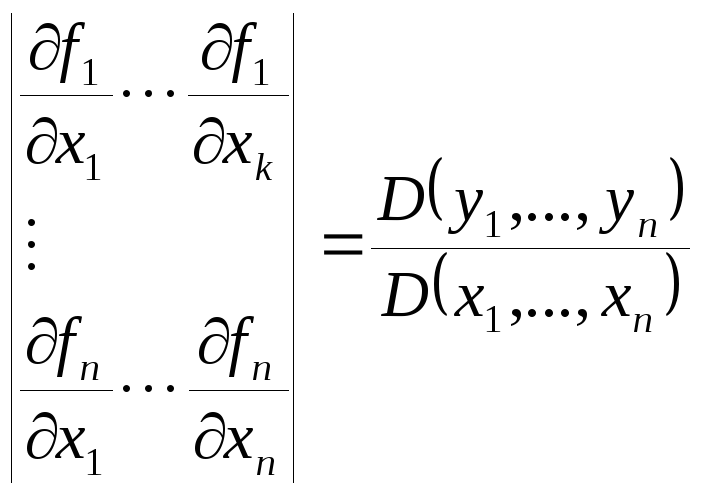называется якобианом отображения.

По доказанному, в случае композиции отображений ,, выполняется равенство

,

Если отображение имеет обратное отображение, т.е. , то , т.е. , если . Эта формула обобщает правило для производной обратной функци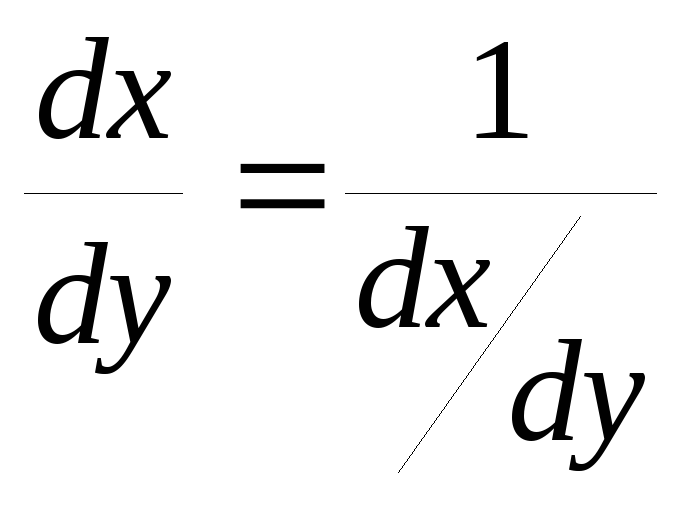и , если .

Отметим важное правило для вычисления якобиана в случае , , , , .

Доказательство этого правила состоит в применении правила дифференцирования сложной функции и последующих алгебраических преобразований. Ввиду громоздкости мы его опускаем.

Вопрос 39. Производные высших порядков

Если функция обладает в некоторой окрестности точки частной производной , а эта производная обозначается . Далее индуктивным образом можно определить производные более высокого порядка. Возникает вопрос: всегда ли ?

Ответ на него такой: нет, не всегда! Можно показать, что функция 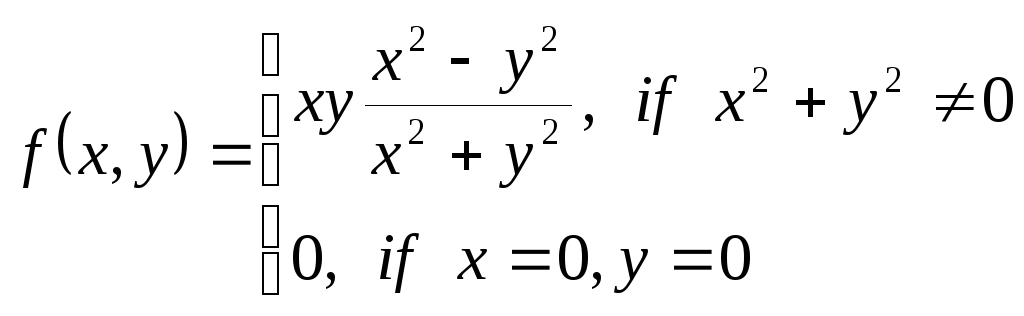имеет неравные производные и . Однако имеет место следующая теорема.

Теорема 39.1. Пусть определена в открытой области и пусть в этой области существуют . Пусть и непрерывны в точке . Тогда в этой точке

Доказательство. Пусть числа такие, что областьсодержит все точки из прямоугольника со сторонами от до и от до . Пусть.

Положим , тогда .

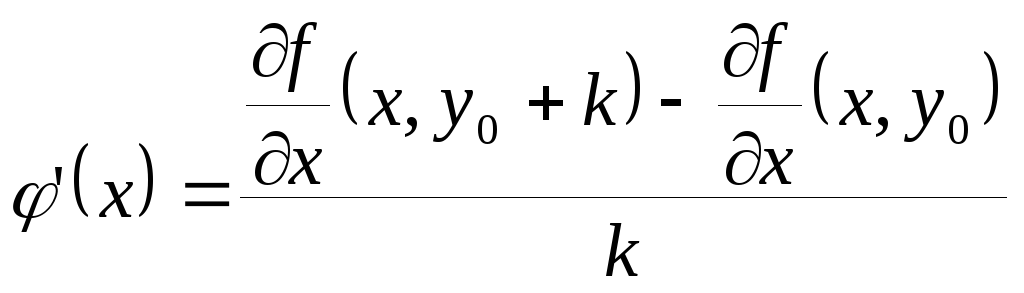В промежутке , по условию теоремы, функция имеет производную . И, значит, непрерывна, причем по теореме Лагранжа (вновь по теореме Лагранжа) , где , .

С другой стороны, аналогично, получаем , где , . Следовательно, устремляя к , получаем, ввиду непрерывности , . Таким образом, теорема доказана.

Замечание. По аналогии можно доказать следующую теорему.

Теорема 39.2. Пусть определена в открытой области и имеет в этой области всевозможные частные производные до -го порядка включительно и смешанные производные -го порядка, причем все эти производные непрерывны в . При этих условиях значение любой -ой смешанной производной не зависит от того порядка, в котором производится последовательное дифференцирование.

Например, и т.п.

Дифференциалы высших порядков

Пусть - имеет непрерывные производные в области . Тогда .(1)

При этом, если - независимые переменные, то можно считать постоянными величинами, не зависящими от . Поэтому , .

Пусть имеет непрерывные частные производные 2-го порядка. Положим по определению

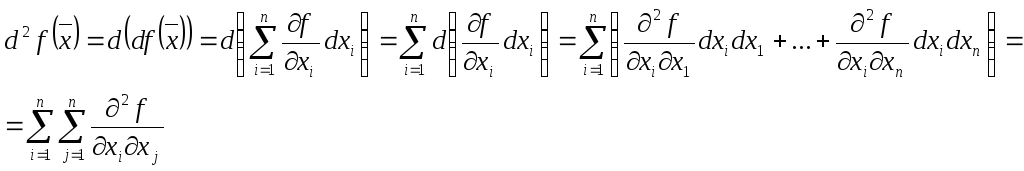
.(2)

Здесь мы воспользовались тем, что .Например, при

, при n=3 .

Вообще, легко заметить, что, используя формальную операторную запись,

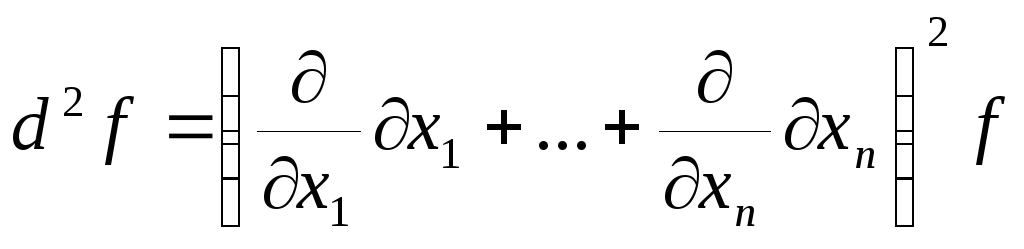(3)

Аналогично, полагая , находим:

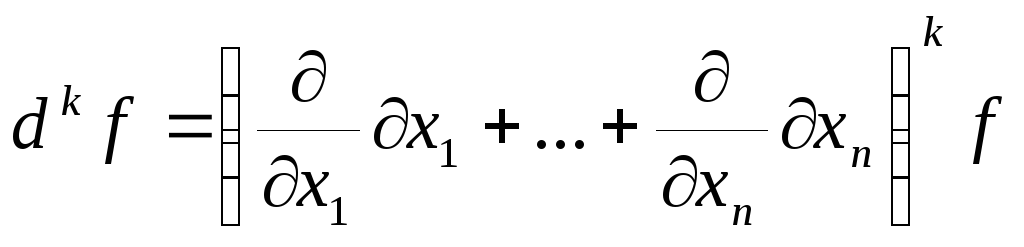(4)

В предположении, что для существуют частные производные до k - го порядка включительно.

Доказательство этого утверждения можно провести индукцией по . Мы не будем подробно останавливаться на этом.

Отметим, что если (т.е. переменные не независимые, а представляют собой функции от других переменных), то , вообще говоря, они не равны 0 и, хотя ввиду инвариантности 1-го дифференциала, формула (1) сохраняется, уже в формулах (2) и (3) (не говоря о (4)) следует внести изменения.

Именно, вместо (3) в этом случае верна формула 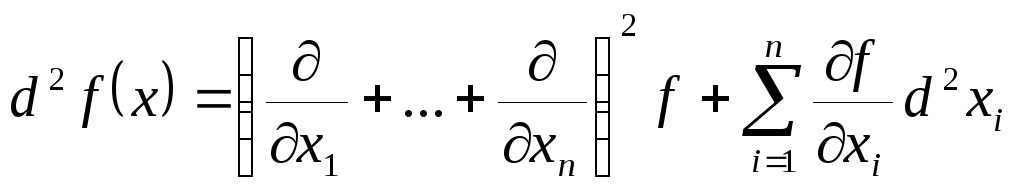(5).

«Добавок» по отношению к (3) получается, из-за того (см. вывод (2)), что в нашем случае .

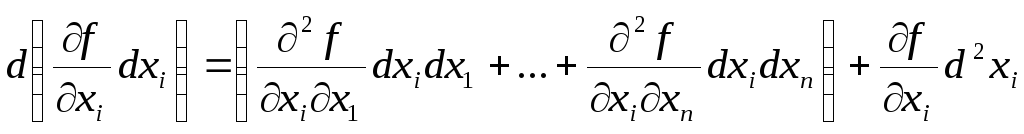Однако, если (6), то и . Поэтому в случае линейной замены переменных (6) формулы (3) и (4) сохраняются.