
- •Геометрические векторы. Основные понятия: определение, модуль,коллинеар- ность, равенство векторов, проекция вектора на направление другого вектора.
- •Линейные операции над геометрическими векторами. Правила треугольника и параллелограмма сложения векторов. Свойства линейных операций.
- •Линейная зависимость системы векторов. Необходимое и достаточное условие линейной зависимости системы векторов (доказательство).
- •Необходимое и достаточное условие линейной зависимости двух; трех векторов.
- •Определение линейного пространства. Размерность линейного пространства.
- •Базис плоскости; базис трехмерного пространства. Линейные операции над векторами в координатной форме.
- •Декартов ортонормированный базис плоскости; трехмерного пространства. Вычисление модуля вектора в ортонормированном базисе.
- •Теорема о вычислении скалярного произведения векторов в ортонормированном базисе
Теорема о вычислении скалярного произведения векторов в ортонормированном базисе
В
евклидовом (унитарном) пространстве
скалярное произведение векторов
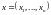 и
и
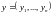 ,
заданных своими координатами в базисе
,
заданных своими координатами в базисе
 ,
вычисляется по правилу
,
вычисляется по правилу
 тогда и только тогда, когда базис
- ортонормированный.
тогда и только тогда, когда базис
- ортонормированный.
Нахождение модуля вектора, угла между векторами с помощью скаляр. произв.
Векторное произведение двух векторов; его свойства. Вычисление векторного произведения векторов в ортонормированном базисе.
Определение.
Векторным произведением 2-х векторов
называется вектор
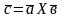 (Х-векторное
произведение)
1.
(Х-векторное
произведение)
1. такой
что
такой
что
Длина вектора c равна S параллелограмма, построена на векторах и .

2. :
3. Направление вектора определяется по правилу буравчика или по правилу правой руки
Если вектор поворачивать к вектору по кратчайшему повороту, то направление правого винта показывает направление вектора .
Свойства векторного произведения.
1)
 ;
;
2)
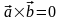 ,
если
ïï
,
если
ïï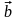 или
=
0 или
=
0;
или
=
0 или
=
0;
3) (m )´ = ´(m ) = m( ´ );
4)
´(
+
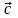 )
=
´
+
´
;
)
=
´
+
´
;
Векторное произведение в координатной форме.
5) Если заданы
векторы
(xa,
ya,
za)
и
(xb,
yb,
zb)
в декартовой прямоугольной системе
координат с единичными векторами
 ,
то
,
то
= =
I*
=
I*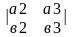 -J*
-J*
 +K*
+K*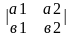 =*
=* =ad-bc
=ad-bc
Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .
Вычисление векторного произведения векторов в ортонормированном базисе.
Смешанное произведение трех векторов; его свойства. Геометрический смысл смешанного произведения.
Определение.
Смешанным
произведением
векторов
,
и
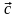 называется число,
равное скалярному произведению вектора
на вектор, равный векторному произведению
векторов
и
.(aXb)c
Обозначается
называется число,
равное скалярному произведению вектора
на вектор, равный векторному произведению
векторов
и
.(aXb)c
Обозначается
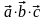 или
(
,
,
).
или
(
,
,
).
Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .v=|abc|
Геометрический смысл заключается в том, что по абсолютной величине смешанное произведение 2-х векторов = объему параллелепипеда, построенных на векторах
Объем этого параллелепипеда = произведению векторов V=| |
Свойства.
1)Смешанное произведение равно нулю, если:
а) хоть один из векторов равен нулю;
б) два из векторов коллинеарны;
в) векторы компланарны.abc=0 ck abc компланарны
2)
3)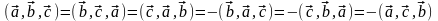
4)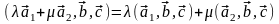
5) Объем треугольной пирамиды, образованной векторами , и , равен

6)Если
 ,
,
 ,
то
,
то
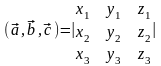
Прямая на плоскости и в пространстве. Канонические и параметрические уравнения прямой. Уравнение прямой, проходящей через две данные точки.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 0. Это уравнение первого порядка называют общим уравнением прямой.
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
Это векторное уравнение может быть представлено в координатной форме:
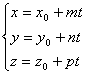
Замечание. Каждые точки на прямой соответствует свое значение параметра t.
При движении точки по прямой параметра t непрерывно меняется.
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
![]() .
.
Замечание. Каждые точки на прямой соответствует свое значение параметра t.
При движении точки по прямой параметра t непрерывно меняется.
Уравнение
прямой проходящей через 2 данные точки.

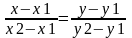
Уравнение плоскости в пространстве (вывод). Уравнение плоскости, проходящей через три данные точки.
Угол между плоскостями. Угол между прямой и плоскостью.

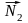
1
0
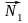
Угол между двумя плоскостями в пространстве связан с углом между нормалями к этим плоскостям 1 соотношением: = 1 или = 1800 - 1, т.е.
cos = cos1.
Определим угол 1. Известно, что плоскости могут быть заданы соотношениями:
 ,
где
,
где
(A1, B1, C1), (A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения:
 .
.
Таким образом, угол между плоскостями находится по формуле:

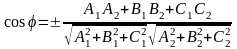
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Угол между прямой и плоскостью.
Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.

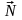
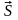
Пусть плоскость задана уравнением
 ,
а прямая -
,
а прямая -
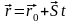 .
Из геометрических соображений (см. рис.)
видно, что искомый угол
= 900 - , где
- угол между векторами
и
.
Этот угол может быть найден по формуле:
.
Из геометрических соображений (см. рис.)
видно, что искомый угол
= 900 - , где
- угол между векторами
и
.
Этот угол может быть найден по формуле:
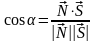
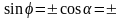
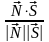

В
координатной форме:
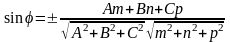
Матрицы. Основные понятия. Виды матриц: прямоугольная, квадратная, единичная, матрица-строка, матрица-столбец. Равенство матриц. Линейные операции над матрицами и их свойства.
Операция умножения матриц; ее свойства. Умножение матрицы-строки на матрицу-столбец. Примеры. Транспонирование матриц. Свойства операции транспонирования.
Определители квадратных матриц, миноры и алгебраические дополнения. Разложение определителя по строке или столбцу. Свойства определителей.
Обратная матрица. Определение, условие существования, алгоритм вычисления. Свойства обратных матриц.
Ранг матрицы (определение). Вычисление ранга матрицы путем приведения ее к ступенчатому виду. Пример.
Системы n линейных уравнений с n неизвестными. Критерий единственности решения. Решение системы n х n методом Крамера.
Запись системы линейных уравнений в виде матричного уравнения. Решение системы n х n матричным способом.
Решение системы m линейных уравнений с n неизвестными методом Гаусса. Пример. Определение числа решений по виду приведенной к ступенчатому виду расширенной матрицы системы.
Однородные системы линейных уравнений. Нахождение нетривиальных (ненулевых) решений системы методом Гаусса. Пример. Условие существования нетривиальных решений. Фундаментальная система решений.
