
- •1.Последовательность. Ограниченные последованности. Монотонные последовательности
- •5.Односторонний предел по Коши
- •7. Определение
- •8. Точки разрыва первого и второго рода
- •13. Производная обратной функции
- •14. Производная параметрически заданной функции
- •16. Дифференциал высшего порядка функции одной переменной
- •[Править]Дифференциал высшего порядка функции нескольких переменных
- •2) Второе достаточное условие
- •3) Третье достаточное условие
- •Функции нескольких переменных
5.Односторонний предел по Коши
Число
 называется правосторонним
пределом (правым
пределом, пределом
справа)
функции
называется правосторонним
пределом (правым
пределом, пределом
справа)
функции  в
точке
в
точке  ,
если для всякого положительного
числа
,
если для всякого положительного
числа  отыщется
отвечающее ему положительное
число
отыщется
отвечающее ему положительное
число 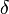 такое,
что для всех
точек
такое,
что для всех
точек  из интервала
из интервала  справедливо неравенство
справедливо неравенство 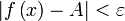 .
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякого положительного числа отыщется отвечающее ему положительное число , такое, что для всех точек из интервала
 справедливо
неравенство
.[1]
справедливо
неравенство
.[1]
![]()
Односторонний предел по Гейне
Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке , если для всякой последовательности
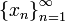 ,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции  сходится
к числу
сходится
к числу  .
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякой последовательности , состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .[1]
![]()
6. 1. Бесконечно малые функции и их сравнение.
Пусть y=f1(x) и y=f2(x) – некоторые две функции, а x стремится к некоторому x0(конечному или бесконечному). Если при этом f1(x)→0 и f2(x)→0, то есть если

Это значит, что f2(x) несравненно меньше f1(x) при x→x0 (f2(x) несравненно быстрее, чем , стремится к нулю при x→x0). В этом случае говорят, что функция f2(x) является бесконечно малой функцией более высокого (высшего) порядка малости, чем функция f1(x),при x→x0. И обозначают этот факт так:
![]()
(читается: f2(x) есть «о малое» от f1(x) при x→x0). Суть записи (4.3) состоит, как сказано выше, в том, что бесконечно малая функция f2(x) является бесконечно малой частью другой бесконечно малой функции f1(x) при x→x0.
7. Определение
Пусть ![]() и
и ![]() .
.
Функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
если для любого
,
если для любого ![]() существует
существует ![]() такое,
что для любого
такое,
что для любого
![]()
Свойства
Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
Если функция непрерывна в точке и
 (или
(или 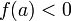 ),
то
),
то  (или
(или  )
для всех
,
достаточно близких к
.
)
для всех
,
достаточно близких к
.Если функции и
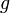 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции  и
и  тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
 ,
то функция
,
то функция  тоже
непрерывна в точке
.
тоже
непрерывна в точке
.Если функция непрерывна в точке и функция непрерывна в точке
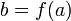 ,
то их композиция
,
то их композиция  непрерывна
в точке
.
непрерывна
в точке
.
8. Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называютточкой разрыва второго рода.
9.
Рассмотрим
функцию ![]() ,
определенную на некотором промежутке
,
определенную на некотором промежутке ![]() .
Функция
непрерывна
в точке
.
Функция
непрерывна
в точке ![]() ,
если предел
функции в
точке
,
если предел
функции в
точке ![]() равен
значению функции в этой точке,
равен
значению функции в этой точке,![]()
Свойства функций, непрерывных на отрезке.
Функция,
непрерывная в каждой точке промежутка ![]() ,
называется непрерывной на промежутке.
Для функции, непрерывной на отрезке
,
называется непрерывной на промежутке.
Для функции, непрерывной на отрезке ![]() ,
справедливы следующие утверждения.
,
справедливы следующие утверждения.
Функция,
непрерывная на отрезке
,
достигает на нем своих наибольшего и
наименьшего значений, т.е. на
отрезке
существуют
точки ![]() такие,
что
такие,
что
![]()
![]() .
.
Если
функция ![]() непрерывна
на отрезке
и
принимает на концах значения разных
знаков, то на интервале
существует
точка
непрерывна
на отрезке
и
принимает на концах значения разных
знаков, то на интервале
существует
точка ![]() ,
в которой функция обращается в нуль,
т.е.
,
в которой функция обращается в нуль,
т.е. ![]() .
Это утверждение применяют для отделения
корней уравнений
.
Это утверждение применяют для отделения
корней уравнений ![]() с
непрерывной левой частью — если найден
отрезок, на концах которого функция
принимает значения разных знаков, то
можно утверждать, что на этом отрезке
есть хотя бы один корень уравнения.
с
непрерывной левой частью — если найден
отрезок, на концах которого функция
принимает значения разных знаков, то
можно утверждать, что на этом отрезке
есть хотя бы один корень уравнения.
Если
функция
непрерывна
на отрезке
, дифференцируема хотя
бы на интервале ![]() ,
то на интервале
существует
точка
,
такая, что
,
то на интервале
существует
точка
,
такая, что ![]() .
Это свойство называют формулой Лагранжа
или формулой конечных приращений.
.
Это свойство называют формулой Лагранжа
или формулой конечных приращений.
Теория Дифференциальной последовательности
10.
1) Физический
смысл производной. Если
функция y = f(x) и ее аргумент x являются
физическими величинами, то производная![]() – скорость изменения переменной y
относительно переменной x в точке
– скорость изменения переменной y
относительно переменной x в точке![]() .
Например, если S = S(t) – расстояние,
проходимое точкой за время t, то ее
производная
.
Например, если S = S(t) – расстояние,
проходимое точкой за время t, то ее
производная![]() –
скорость в момент времени
–
скорость в момент времени![]() .
Если q = q(t) – количество электричества,
протекающее через поперечное сечение
проводника в момент времени t,
то
.
Если q = q(t) – количество электричества,
протекающее через поперечное сечение
проводника в момент времени t,
то![]() – скорость изменения количества
электричества в момент времени
,
т.е. сила тока в момент времени
.2) Геометрический
смысл производной.
– скорость изменения количества
электричества в момент времени
,
т.е. сила тока в момент времени
.2) Геометрический
смысл производной.
Пусть ![]() –
некоторая кривая,
–
некоторая кривая,![]() –
точка на кривой
.
–
точка на кривой
.
Любая прямая, пересекающая не менее чем в двух точках называется секущей.
Касательной
к кривой
в
точке
называется
предельное положение секущей ![]() ,
если точка
,
если точка ![]() стремится
к
,
двигаясь по кривой.
стремится
к
,
двигаясь по кривой.
Из определения очевидно, что если касательная к кривой в точке существует, то она единственная
11.
1)
Производная константы равна нулю, т.е ![]() ,
где C – константа.
,
где C – константа.
2)
Производная суммы (разности) равна сумме
(разности) производных, т.е ![]() .
3) Производная произведения находится
по правилу:
.
3) Производная произведения находится
по правилу: ![]() .
.
4) ![]() ,
где
,
где ![]() -
константа. 5) Производная
дроби находится по правилу:
-
константа. 5) Производная
дроби находится по правилу:![]() .
.
6)
Если функция![]() имеет
производную в точке
имеет
производную в точке![]() ,
а функция
,
а функция![]() имеет
производную в точке
имеет
производную в точке![]() ,
то сложная функция
,
то сложная функция![]() имеет
производную в точке
,
причем
имеет
производную в точке
,
причем ![]() (правило
дифференцирования сложной функции).
(правило
дифференцирования сложной функции).
7)
Пусть функция y = f(x) имеет производную
в точке
,
причем ![]() .
Если существует обратная функция
.
Если существует обратная функция ![]() ,
то она имеет производную в
точке
,
то она имеет производную в
точке![]() и
и ![]() (производная
обратной функции).
(производная
обратной функции).
12.
Цепное
правило (правило
дифференцирования сложной функции)
позволяет вычислить производную
композиции двух и более функций на
основе индивидуальных производных.
Если функция f имеет производную в
точке ![]() ,
а функция g имеет производную в точке
,
а функция g имеет производную в точке ![]() ,
то сложная функция h(x) = g(f(x)) также имеет
производную в точке
. Т
е о р е м а 1. Если функция
,
то сложная функция h(x) = g(f(x)) также имеет
производную в точке
. Т
е о р е м а 1. Если функция ![]() имеет
производную в точке
имеет
производную в точке ![]() ,
а функция
,
а функция ![]() имеет
производную в точке
имеет
производную в точке ![]() ,
то сложная функция
,
то сложная функция
![]() (1)
(1)
имеет производную (по ) в точке и справедливо равенство
![]() (2)
(2)
или
![]() .
(3)
.
(3)
