Свойства бесконечно малых величин

1. Алгебраическая сумма конечного числа бесконечного малых величин есть величина бесконечно малая.

По условию и - бесконечно малые величины при . Это означает, что для любого найдутся такие числа , что для всех и удовлетворяющих условиям:

и (1.1)

выполняются соответствующие неравенства:

и . (1.2)

Если взять в качестве числа минимальное из чисел и , т.е. , то неравенству будут удовлетворять решения обоих неравенств (1.1) , а, следовательно, одновременно будут верны неравенства (1.2). Складывая почленно неравенства (1.2), получим, что;

.

Используя свойство абсолютных величин, т.е. , придем к более сильному неравенству:

(1.3)

Итак, для любого существует такое , что для всех и удовлетворяющих условию верно неравенство (1.3). А это означает, что функция есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную функцию (в т.ч. на постоянную, на другую бесконечно малую) есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Отношение двух бесконечно малых (неопределенность вида ) в зависимости от характера изменения переменных в числителе и знаменателе может оказаться или числом, или бесконечно малой или бесконечностью.

Сравнение бесконечно малых

        Пусть   и   — бесконечно малые при  . 1. Если  , то говорят, что   является бесконечно малой высшего порядка по сравнению с  . В этом случае пишут  . 2. Если  , где  —число, отличное от нуля, то говорят, что   и  — бесконечно малые одного и того же порядка. В часности, если  , то бесконечно малые   и   называются эквивалентными. Запись  ~  означает, что   и  —эквивалентные бесконечно малые.          Если  , то это означает, что  . Таким образом,   является бесконечно малой высшего порядка по сравнению с  , т. е.  3. Если   и  —бесконечно малые одного и того же порядка, причем  , то говорят, что бесконечно малая   имеет порядок   по сравнению с  . Отметим некоторые свойства бесконечно малых величин: 1^o. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если  , то   и  . 2^o. Бесконечно малые   и   эквивалентны тогда и только тогда, когда их разность  является бесконечно малой высшего порядка по сравнению с   и  , т. е. если  ,  . 3^o. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, т.е. если  ,  ~ ,  ~ , то  .

24. Замечательные пределы: число е. Следствия из 2-го замечательного предела. Второй замечательный предел.

Определение. Числом (вторым замечательным пределом) называется предел числовой последовательности :

, где

Прямым вычислением можно убедиться, что , (иррациональное число, число Эйлера).

Если рассмотреть функцию , то при функция имеет предел, равный числу :

.

Или если , то .

Непосредственное вычисление этого предела приводит к неопределенности . Однако доказано, что он равен числу . Второй замечательный предел необходимо всегда использовать при раскрытии неопределенности вида .

Число (число Эйлера, неперово число) играет важную роль в математическом анализе. График функции

Рассмотрим примеры вычисления пределов. Получил название экспоненты. Широко используются логарифмы по основанию , называемые натуральными. Натуральные логарифмы обозначаются символом .
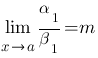