25. Непрерывность функции. Точки разрыва 1-го и 2-го рода.

2. Если   не существует, то точку x₀ ϵ X называем точкой существенного разрыва функции f. При этом

а) если существуют конечные пределы

f(x₀ - 0),   f(x₀ + 0)   (f(x₀ - 0) ≠ f(x₀ + 0)),

то точку x₀ называем точкой разрыва первого рода функции f;

б) все остальные точки существенного разрыва называем точками разрыва второго родафункции f.

Поскольку в изолированной точке x₀ ϵ X функция f: X → R непрерывна, то ее точками разрыва могут быть лишь предельные точки x ϵ X.

Основные свойства непрерывных функций

Функция f: [a, b] → R называется непрерывной на сегменте [a, b], если она непрерывна на интервале ]a, b[ и в точке a непрерывна справа, а в точке b - слева.

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], тогда:

1) она ограничена на этом сегменте;

2) если  , то на сегменте [a, b] существуют точки x₁ и x₂ такие, что f(x₁) = m, f(x₂) = M (теорема Вейерштрасса);

3) она принимает на каждом сегменте  , все промежуточные значения между f(α) и f(β) (теорема Коши).

В частности, если f(α)f(β) < 0, то найдется такое значение γ (α < γ < β), то f(γ) = 0.

Функция f: ]a, b[ → R называется кусочно-непрерывной на интервале ]a, b[, если она непрерывна во всех точках этого интервала, кроме конечного числа точек разрыва первого рода и конечного числа точек устранимого разрыва.

26. Понятие производной. Геометрический и механический смысл. Определение производной

Пусть на некотором промежутке Х определена функция y=f(x). Возьмем любую точку _. Зададим аргументу х произвольное приращение ∆х ≠ 0 такое, что точка х+∆х также будет принадлежать Х. Функция получит приращение ∆у= f(x+∆х)− f(x).

Определение. Производной функции y=f(x) в точке х называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует).

Для обозначения производной функции y=f(x) в точке х используются символы у′(х) или f′(x).

Итак, по определению, .

Если для некоторого значения х₀ выполняется условие

или ,

т.е. пределы равны бесконечности, то говорят, что в точке х₀ функция имеет бесконечную производную.

Если функция y=f(x) имеет конечную производную в каждой точке , то производную f′(x) можно рассматривать как функцию х, также определенную на Х. Нахождение производной функции называется дифференцированием функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки –известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +    точка перемещается на расстояние:  x ( t₀ +   ) - x ( t₀ ) =  , а её средняя скорость равна:  v_a =   /   .При      0  значение средней скорости стремится к определённой величине, которая называетсямгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

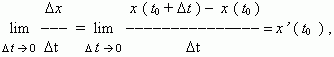
отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной. Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).