5.6 Вопросы для самопроверки знаний

по лабораторной работе №3

1. Дать определение коэффициента корреляции.

2. Дайте определение корреляционной зависимости между двумя случайными величинами (геологическими параметрами) и .

3. Записать систему нормальных уравнений для нахождения параметров 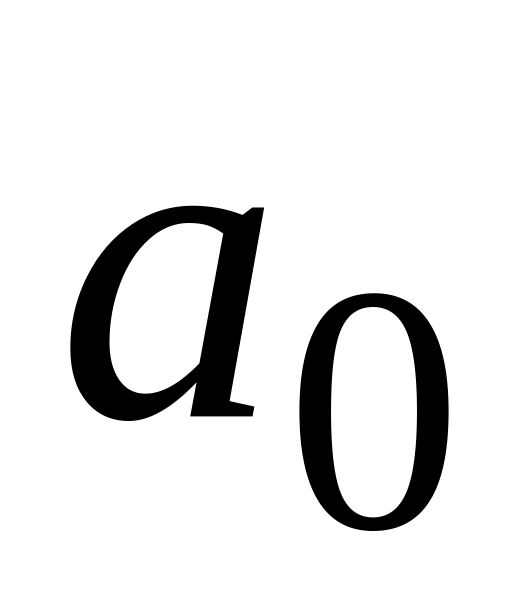и уравнения линейной регрессии .

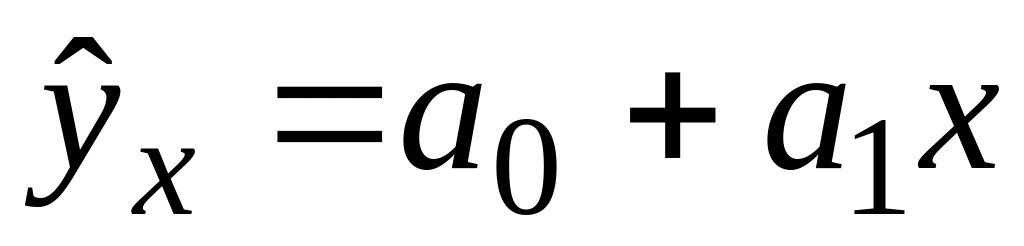4. Сформулировать свойства коэффициента корреляции.

5. Рассказать, как определяется теснота линейной корреляционной связи между двумя параметрами на основе коэффициента корреляции.

6. Как производится оценка коэффициента и уравнения линейной регрессии ?

6. Задание 4. Оценка коэффициентов линейной

ЗАВИСИМОСТИ МЕЖДУ ГЕОЛОГИЧЕСКИМИ ПАРАМЕТРАМИ

6.1 Цель работы

Научиться находить оценки параметров линейной регрессии методом наименьших квадратов, если между случайными параметрами и существует линейная корреляционная зависимость и они ( и ) подчинены нормальному закону распределения.

6.2. Основные теоретические положения

Пусть эмпирическая зависимость между признаками X и Y задана таблицей Х | x₁ x₂ …x_n

Y | y₁ y₂ …y_n (6.1)

и пусть по графику этой зависимости видно, что ее можно аппроксимировать линейной функцией (построить линейное уравнение регрессии, линейный тренд)

. (6.2)

Для определения коэффициентов уравнения (6.2) по наблюденным данным (6.1) в геологии используется метод наименьших квадратов (МНК).

Согласно этому методу, коэффициенты ₀ и ₁ находятся из условия минимума среднеквадратичного отклонения наблюденных значений признака Y от теоретических (расчетных) i=1, 2,…, n:

. (6.3)

Коэффициенты, удовлетворяющие требованию (6.3), находятся как решение системы линейных уравнений:

. (6.4)

Теперь рассмотрим задачу оценки качества уравнения регрессии. Качество регрессии (аппроксимации, тренда) определяется величинами отклонений эмпирических значений от расчетных . Значения часто называют остатками. Анализ остатков осуществляется либо графически, т. е. визуально, либо аналитически.

При визуальном анализе остатков строятся точечные диаграммы в координатах , , по которым выявляется наличие резкоуклоняющихся значений, гетероскедастичности данных или других закономерностей в поведении остатков.

При аналитическом анализе остатков вычисляется среднее значение квадратов остатков, которое называется остаточной дисперсией:

. (6.5)

Корень квадратный из остаточной дисперсии называют остаточным среднеквадратичным отклонением и обозначают .

В случае линейной регрессии формула для вычисления S²_ост имеет вид:

, (6.6)

где коэффициенты и получены при решении нормальной системы уравнений (6.4).

При заданном допустимом (пороговом) значении дисперсии регрессия считается качественной, если вычисленное по формуле 6.5 или 6.6 значение S²_ост не превышает это пороговое значение, т. е. если  . В геологии обычно не задано, поэтому для оценки качества регрессии используется коэффициент детерминации ( ):

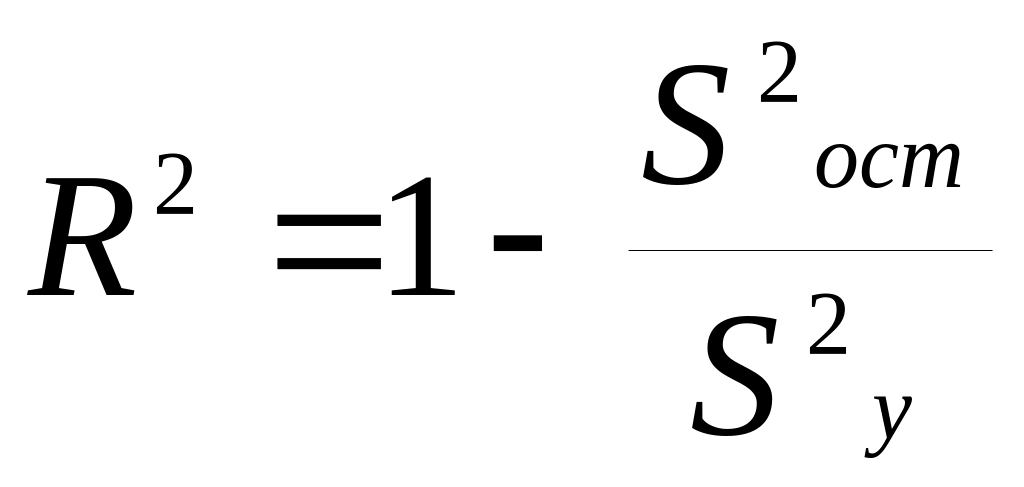, (6.7)

здесь - дисперсия признака , которая характеризует степень разброса значений вокруг математического ожидания М(у) и вычисляется по формуле:

. (6.8)

Качество уравнения регрессии по значению оценивается в соответствии с табл. 6.1.

Таблица 6.1

Градации коэффициента детерминации для оценки качества регрессии

Градации	Теснота связи
=1	Связь функциональная
0,56 1	Связь тесная
0,25 0,56	Связь средней тесноты
0,12 0,25	Связь слабая
0,12	Связи нет

Для проверки значимости используется статистика F, которая имеет распределение Фишера:

. (6.9)

Для проверки гипотезы необходимо вычислить и по таблице приложения 2 найти 1, . Если  1, - нет основания отвергать нулевую гипотезу.

6.3 Пример. В результате опытов получены следующие данные о зависимости растворимости (У) азотно-натриевой соли от температуры (t⁰C).

t^0C	0	4	10	15	21	29	36	51	68
У	66.7	71.0	76.3	80.6	85.7	92.9	99.4	113.6	125.1

Нанеся эти данные на график, получим точки, расположенные довольно близко к некоторой прямой (рис. 6.1).

Р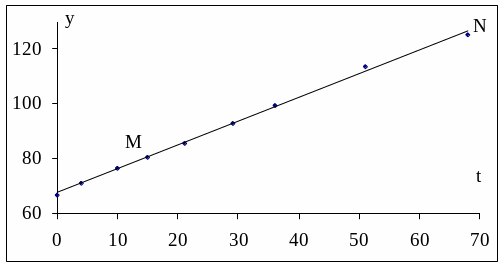 ис. 6.1 Эмпирическая и регрессионная линейная зависимость

Вычислим коэффициенты аппроксимирующей функции

по МНК. Расчеты по этому методу сведены в табл. 6.2.

Таблица 6.2

Вычисление по методу наименьших квадратов

№	хi	xi^2	yi	xiyi
1	0	0	66.7	0
2	4	16	71.0	284
3	10	100	76.3	763
4	15	225	80.6	1209
5	21	441	85.7	1799.7
6	29	841	92.9	2694.1
7	36	1296	99.4	3578.4
8	51	2601	113.6	5793.6
9	68	4624	125.1	8506.8
	234	10144	811.3	24628.6

Система для вычисления коэффициентов и МНК имеет вид:

.

Решая ее, получим , , т. е. прямая линия описывается уравнением: .

Для оценки качества регрессии вычислим S²_ост (формула (6.6)) и R² (формула 6.7). Вычисления и результаты приведены в табл. 7.3, , .

Таблица 6.3

Вычисление отклонений замеренных значений от прямой линии

№ п/п
1	0	66.7	67.5	-0.8	0.64
2	4	71.0	70.98	0.02	0.0004
3	10	76.3	76.2	0.1	0.01
4	15	80.6	80.55	0.05	0.0025
5	21	85.7	85.77	-0.07	0.0049
6	29	92.9	92.73	0.17	0.0289
7	36	99.4	98.82	0.58	0.3364
8	51	113.6	111.87	0.73	2.9929
9	68	125.1	126.66	-1.56	2.4336
=6.450

Для проверки гипотезы о значимости вычислим (по 6.9), затем найдем из приложения 2 . Так как  гипотеза отвергается, т.е. значение значимо.