4.13. Специальные классы булевских функций определение

Множество функций B называется замкнутым классом, если [B] = B.

Например, множество {x, } является замкнутым классом. Рассмотрим пять специальных классов булевских функций, свойства которых будут использованы при нахождении простых необходимых и достаточных условий полноты произвольных систем функций в P₂.

4.13.1. Функции, сохраняющие ноль

Обозначим как Т₀ множество всех таких булевских функций, которые на нулевом наборе значений переменных принимают значение 0.

О таких функциях говорят, что они сохраняют 0, т.е. множество б.ф., сохраняющих ноль, это:

Т₀ = {f(x₁,...,x _n)  f(0,...,0) = 0}.

Сформулируем простейшие свойства класса T₀.

1. Класс T₀ является замкнутым классом функций.

Для проверки справедливости последнего утверждения достаточно проверить, что всякая формула U(f₁, . . . , f_p), составленная с помощью функций f₁, . . . , f_p, сохраняющих ноль, представляет функцию f_U, которая также сохраняет ноль.

Проведем обоснование этого свойства в соответствии с определением понятия формулы над классом функций.

1. Если U = f(x₁,. . . , x_n), где f(x₁, . . . , x_n)T₀, то f (0, . . . , 0) = 0 и f_U = f.

2. Если U = f (U₁,..., U_n), где f (x₁, . . . , x _n)  T₀, а U₁, . . . , U_n  это или символы переменных или подформулы формулы U, составленные с помощью функций из T₀ и символов переменных. Заметим, что поскольку обозначение переменной представляет тождественную функцию I(x) = x, то U₁, . . . , U_n можно рассматривать как подформулы, представляющие некоторые функции 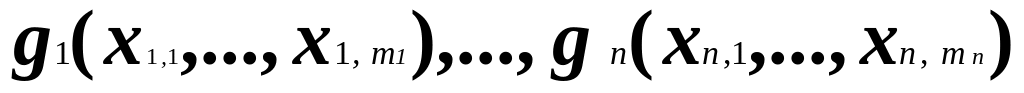из класса T₀. Тогда функция f( ) также принадлежит классу T₀.

Действительно, f(g₁(0,. . . , 0), . . . , g_n (0, . . . ,0))= f(0, . . . ,0)=0.

2. Определим число различных функций переменных x₁, . . . , x_n, которые содержатся в T₀.

Поскольку функции из T₀ на всех наборах значений переменных, отличных от нулевого набора, принимают произвольные значения, и таких ненулевых наборов 2ⁿ1, то в T₀ содержится ровно различных булевских функций n переменных.

4.13.2. Функции, сохраняющие единицу

Обозначим как T₁ множество всех булевских функций, которые на единичном наборе значений переменных принимают значение 1. О таких булевских функциях говорят, что они сохраняют единицу, т.е. Т₁ = {f(x₁, . . . , x_n)  f(1, . . . , 1) = 1}.

Класс T₁ является замкнутым и содержит различных функций n переменных. Последние свойства могут быть обоснованы аналогично тому, как это делалось для класса T₁.

4.13.3. Самодвойственные функции

Двоичные наборы и называются противоположными наборами.

Противоположные наборы значений переменных в табличном задании булевых функций соответствуют строкам, расположенным симметрично относительно середины таблицы.

Докажем это утверждение. Заметим, что середина таблицы располагается между последним набором верхней половины таблицы (0, 1, . . . , 1) и первым набором значений переменных в нижней половине таблицы (1, 0,. . . , 0).

Тогда, пусть и  произвольные противоположные наборы. Для определенности будем считать, что ₁ =0.

1. Для набора , расположенного в верхней половине таблице, определим расстояние до нижнего набора верхней половины таблицы, т.е. количество наборов до набора (0, 1, . . . , 1). Нетрудно видеть, что искомое расстояние представляется числом, имеющим двоичное представление в виде набора .

2. Определим двоичный набор, находящийся на таком же расстоянии от набора (1,0, . . . , 0), являющегося первым набором нижней половины таблицы

Нетрудно проверить, что 10. . . 0 + = .

Следовательно, набор, отстоящий от (1, 0, . . . , 0) на расстоянии ,  это набор, который является противоположным . Поэтому расстояния от противоположных наборов и до середины таблицы равны.