
- •Глава 2. Исследование устойчивости и качества сау
- •2.1. Устойчивость динамических систем
- •2.2. Критерии устойчивости
- •2.2.1. Аналитические критерии устойчивости
- •2.2.2. Частотные критерии устойчивости
- •2.3. Показатели качества сау и методы их определения
- •Интегральные оценки показателей качества
- •Частотные методы оценки показателей качества
- •2.4. Чувствительность систем автоматического управления
2.2.2. Частотные критерии устойчивости
При исследовании устойчивости линейных САР, которые описываются дифференциальными уравнениями высоких порядков, использование аналитических критериев оказывается весьма трудоемким. Частотные критерии получили наиболее широкое практическое применение. Это обусловлено их положительными свойствами, такими как:
позволяют судить об устойчивости замкнутой системы по более простой передаточной функции разомкнутой системы;
анализ устойчивости можно выполнять по экспериментально определенным частотным характеристикам;
с помощью частотных характеристик можно судить и о качестве переходных процессов в САР.
В основе частотных критериев устойчивости лежит известный в теории функций комплексного переменного принцип аргумента. Пусть дано характеристическое уравнение вида
![]() (2.10)
(2.10)
Уравнение (2.10) – это алгебраическое уравнение с действительными коэффициентами.
Многочлен
![]() можно представить в виде выражения
можно представить в виде выражения
![]() (2.11)
(2.11)
где
![]() –
корни
уравнения (2.11).
–
корни
уравнения (2.11).
Произведем
замену
![]() (j
- уравнение
мнимой оси), тогда получим
(j
- уравнение
мнимой оси), тогда получим
![]() (2.12)
(2.12)
Рассмотрим
представление комплексного числа
![]() на
комплексной плоскости. Начало вектора,
изображающего это число, лежит в точке
,
а конец - на мнимой оси в точке j.
Геометрически это представление показано
на рис. 2.6.
на
комплексной плоскости. Начало вектора,
изображающего это число, лежит в точке
,
а конец - на мнимой оси в точке j.
Геометрически это представление показано
на рис. 2.6.
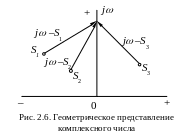
Найдем аргумент комплексного числа
![]() (2.13)
(2.13)
При изменении в пределах от - до + аргумент будет изменяться в соответствии с выражением
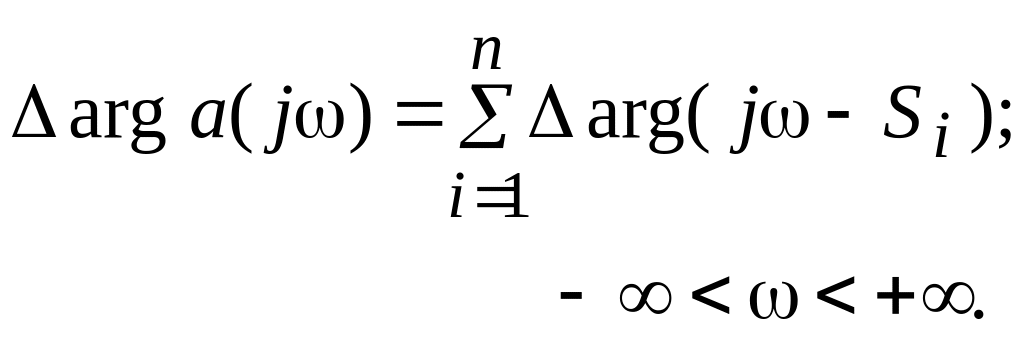 (2.14)
(2.14)
Согласно (2.14) для подсчета изменения аргумента надо подсчитать сумму изменений аргументов выражений вида . Это изменение аргумента зависит от того, в какой полуплоскости лежит корень . Рассмотрим эти два случая. Корень лежит в левой полуплоскости, как это показано на рис. 2.7 а.
При изменении от - до + конец вектора скользит вдоль мнимой оси снизу вверх, поворачиваясь против часовой стрелки на 180 и, следовательно, изменение аргумента при этом будет
![]() (2.15)
(2.15)
Если корень лежит в правой полуплоскости (рис. 2.7 б), то
![]() (2.16)
(2.16)
Допустим,
что уравнение
![]() имеет m
корней
в правой полуплоскости и
l
корней в левой. При этом
l+m=n.
Тогда на основании (2.12), (2.15) и (2.16) получим
имеет m
корней
в правой полуплоскости и
l
корней в левой. При этом
l+m=n.
Тогда на основании (2.12), (2.15) и (2.16) получим
![]() (2.17)
(2.17)
Уравнение
(2.17) представляет собой выражение
принципа аргумента, который формулируется
следующим образом: изменение
аргумента
![]() при
изменении
от
-
до +
равно разности между числом корней l,
лежащих в левой полуплоскости и числом
корней m,
лежащих в правой полуплоскости, умноженной
на .
при
изменении
от
-
до +
равно разности между числом корней l,
лежащих в левой полуплоскости и числом
корней m,
лежащих в правой полуплоскости, умноженной
на .
Критерий А.В.Михайлова.
Был сформулирован им в 1938 году. Он является по существу геометрической интерпретацией принципа аргумента. Пусть дано характеристическое уравнение системы
(2.18)
Полином называется, как было отмечено выше, характеристическим полиномом. Для того чтобы система была устойчива, необходимо, чтобы все корни характеристического уравнения лежали в левой полуплоскости, т.е. чтобы m=0. В этом случае согласно (2.17) должно удовлетворяться уравнение
![]() (2.19)
(2.19)
Из
условия (2.19) следует, что все корни
уравнения
лежат в левой полуплоскости. Геометрическое
место конца вектора
при
![]() называется годографом вектора
или
годографом
Михайлова.
Согласно (2.18) уравнение годографа
Михайлова имеет вид
называется годографом вектора
или
годографом
Михайлова.
Согласно (2.18) уравнение годографа
Михайлова имеет вид
![]() (2.20)
(2.20)
где действительная и мнимая части комплекса будут
![]()
Действительная часть является четной функцией
![]()
а мнимая часть является нечетной функцией
![]()
Следовательно
![]() т.е.
т.е.
![]() и
и
![]() являются сопряженными комплексными
величинами, и
являются сопряженными комплексными
величинами, и
![]() (2.21)
(2.21)
Учитывая (2.21), уравнение (2.19) можно записать в виде
![]() (2.22)
(2.22)
Из
формулы следует формулировка критерия
устойчивости Михайлова. Система
автоматического регулирова-ния устойчива,
если при изменении
от
0 до +
вектор
поворачивается на угол
![]() ,
где n
– степень характеристического уравнения;
или, иначе, если годограф
с ростом
от
0 до +,
начинаясь на действительной оси, обходит
последовательно в положительном
направлении (против часовой стрелки) n
квадрантов комплексной плоскости. На
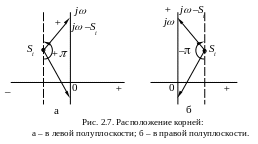
рис. 2.8 а показаны годографы
устойчивых САР для разных n.
На рис. 2.8 б показаны годографы неустойчивых
САР. Годограф
можно построить по выражениям для
,
где n
– степень характеристического уравнения;
или, иначе, если годограф
с ростом
от
0 до +,
начинаясь на действительной оси, обходит
последовательно в положительном
направлении (против часовой стрелки) n
квадрантов комплексной плоскости. На
рис. 2.8 а показаны годографы
устойчивых САР для разных n.
На рис. 2.8 б показаны годографы неустойчивых
САР. Годограф
можно построить по выражениям для
![]() и
и
![]() ,
задаваясь значениями .
,
задаваясь значениями .
Пример. С помощью критерия Михайлова необходимо исследовать устойчивость САР, структурная схема которой показана на рис. 2.9 а. Это система стабилизации движения корабля по курсу.

Характеристический полином замкнутой системы будет иметь вид
![]()
Произведя замену , получим
![]()
Для построения кривой Михайлова выделим вещественную и мнимую части:

Зададимся следующими параметрами звеньев:
К1 =1,2; К2 =0,6; К3 =1; К4 =1; Т1 =0,1с; Т2 =0,05с; Т3 =1с.
Изменяя от 0 до , построим кривую Михайлова. Ее вид показан на рис. 2.9 б. Уравнение исследуемого контура имеет четвертый порядок. Годограф Михайлова обходит последовательно против часовой стрелки четыре квадранта, начиная с положительной вещественной оси. Значит САР является устойчивой.
Критерий Найквиста.
Пусть передаточная функция разомкнутой САР имеет вид:
![]()
Образуем функцию следующего вида
![]() (2.23)
(2.23)
Числитель этой функции (2.23) представляет собой характеристический полином замкнутой системы, знаменатель - характеристический полином разомкнутой системы. Пусть степень с(S) равна n, а степень b(S) равна r. Из физических соображений следует, что r<n. Учитывая неравенство r<n, можно утверждать, что степень полинома c(S)+b(S) также равна n. Предположим, что САР в разомкнутом состоянии устойчива. Тогда согласно критерию Михайлова изменение аргумента характеристического полинома разомкнутой системы будет
![]()
![]()
Если потребовать, чтобы система в замкнутом состоянии была устойчивой, то должно удовлетворяться равенство
![]() .
(2.24)
.
(2.24)
Из (2.23) следует, что
![]() (2.25)
(2.25)
Значит,
САР устойчива, если изменение аргумента
вектора F(j)
при
изменении
от 0 до ,
равно нулю. На рис. 2.10 а показаны два
годографа
![]() Первый соответствует устойчивой САР:
он не охватывает точку (0,
0),
второй –неустойчивой: он охватывает
точку (0,
0).
Так как F(j)
отличается от
Первый соответствует устойчивой САР:
он не охватывает точку (0,
0),
второй –неустойчивой: он охватывает
точку (0,
0).
Так как F(j)
отличается от
![]() на +1,
то сказанное можно сформулировать
непосредственно для характеристики
– см. рис. 2.10 б.
на +1,
то сказанное можно сформулировать
непосредственно для характеристики
– см. рис. 2.10 б.
Замкнутая система устойчива, если годограф разомкнутой САР не охватывает точку (-1, j0).

Пример. С помощью критерия Найквиста необходимо исследовать устойчивость системы регулирования, для которой передаточная функция в разомкнутом виде
![]()
О пределим
предельный коэффициент усиления, при
котором САР устойчива. Частотные
годографы для этой системы при разных
К
показаны на рис. 2.11.
пределим
предельный коэффициент усиления, при
котором САР устойчива. Частотные
годографы для этой системы при разных
К
показаны на рис. 2.11.
Согласно критерию Найквиста, при К=К1 система устойчива, при К=К2 – неустойчива. Для определения предельного значения Кпр необходимо найти значение К, при котором годограф проходит через точку (-1, j0), т.е. решить уравнение
Составив уравнения для мнимых и действительных частей, находим и Кпр:
![]()
Метод Д-разбиения.
Пусть дано характеристическое уравнение n-й степени
![]()
При заданном значении коэффициентов уравнения в общем случае оно имеет m корней в правой полуплоскости и (n-m) корней в левой полуплоскости. При изменении коэффициентов уравнения корни его перемещаются в плоскости корней, описывая корневые годографы. При определенном значении коэффициентов один из корней попадает в начало координат или пара корней попадает на мнимую ось и поэтому значения этих коэффициентов удовлетворяют уравнению:
![]() (2.26)
(2.26)
Уравнению
(2.26) в n-1
- мерном
пространстве коэффициентов, по осям
которого отложены а0,
а2,
…, аn-1,
соответствует
точка при данном значении
и гиперповерхность - при изменении
от -
до +
.
Если перемещаться в пространстве
коэффициентов, т.е. если менять коэффициенты
уравнения, то при некотором их значении
мы пересечем гиперповерхность
![]() и, значит, пара (или один корень) будет
переходить из правой (левой) полуплоскости
корней в левую (правую), т.е. пересекать
границу устойчивости. Пусть n=3,
тогда
и, значит, пара (или один корень) будет
переходить из правой (левой) полуплоскости
корней в левую (правую), т.е. пересекать
границу устойчивости. Пусть n=3,
тогда
![]()
 Каждому
значению коэффициентов а0,
а1
и
а2
в трехмерном пространстве коэффициентов
соответствует точка, как это показано
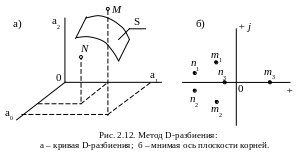
на рис. 2.12 а. Этому значению коэффициентов
уравнения соответствует определенное
расположение корней в плоскости корней
(рис. 2.12 б).
Каждому
значению коэффициентов а0,
а1
и
а2
в трехмерном пространстве коэффициентов
соответствует точка, как это показано
на рис. 2.12 а. Этому значению коэффициентов
уравнения соответствует определенное
расположение корней в плоскости корней
(рис. 2.12 б).
Точке М соответствуют корни m1, m2 и m3; точке N - корни n1, n2 и n3. При некоторых значениях коэффициентов один или пара корней окажутся на мнимой оси, т.е. корни будут иметь вид 0 или j1 и, следовательно, соответствующая точка в пространстве коэффициентов будет удовлетворять уравнению:
![]()
Этому уравнению при - соответствует поверхность S. При изменении коэффициентов корни тоже изменяются и попадают на мнимую ось только тогда, когда точка в пространстве коэффициентов попадает на поверхность S. При пересечении такой поверхности корни переходят из одной плоскости в другую. Можно сделать вывод о том, что поверхность S разделяет пространство коэффициентов на области, каждой точке которых соответствует характеристическое уравнение 3-й степени, имеющее определенное число корней в правой и левой части плоскости корней. Обозначим эти области - D(m), где m - число корней уравнения в правой полуплоскости. Для нашего примера можно наметить в пространстве коэффициентов четыре области: D(3), D(2), D(1), D(0). Последняя область является областью устойчивости. Такое разбиение пространства на области с различным значением m называется D-разбиением. Переход через границу D-разбиения соответствует переходу корней уравнения через мнимую ось. В некоторых случаях необходимо выяснить влияние одного параметра на устойчивость САР. Обозначим этот параметр через v. Предположим, что этот параметр входит линейно в характеристическое уравнение вида
![]() (2.27)
(2.27)
Границы D-разбиения, согласно уравнению (2.26), определяются с помощью выражения
![]() (2.28)
(2.28)
Отсюда
 (2.29)
(2.29)
При
построении границы
D-разбиения
достаточно построить ее для положительных
значений
и дополнить зеркальным отображением
построенного участка относительно
действительной оси. Обычно нас интересует
D-разбиение
не всей комплексной плоскости параметра
v,
а лишь ее действительной оси, которой
соответствуют действительные значения
v.
На
рис. 2.13 показан вид границы D-разбиения
в плоскости
![]() .
При изменении
от –
до +
в плоскости S
мнимая
ось проходит снизу вверх, при этом левая
полуплоскость остается слева. Будем
штриховать мнимую ось слева, как это
показано на рис. 2.13 б.
.
При изменении
от –
до +
в плоскости S
мнимая
ось проходит снизу вверх, при этом левая
полуплоскость остается слева. Будем
штриховать мнимую ось слева, как это
показано на рис. 2.13 б.
Такому движению по мнимой оси соответствует движение по границе D-разбиения в плоскости v (рис. 2.13а), которую будем также штриховать слева по обходу при изменении от – до +. Если в плоскости v пересекать границу D-разбиения по направлению штриховки (стрелка 1, рис. 2.13 а), то в плоскости корней S один корень переходит из правой полуплоскости в левую. Если в плоскости v пересекать границу D-разбиения против штриховки (стрелка 2, рис. 2.13 а), то в плоскости корней S один корень переходит из левой полуплоскости в правую. Направление штриховки и число штриховок определяют направление перехода корней через мнимую ось и их число. Поэтому для разметки областей D(m) достаточно знать распределение корней относительно мнимой оси при каком-либо произвольном значении параметра.
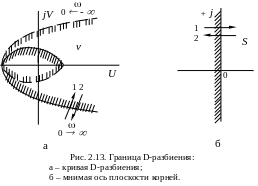
Переходя в плоскости v от этого значения параметра v к любому другому, по числу пересечений границы D-разбиения и направлению штриховки, можно определить значение m в любой точке. Областью устойчивости будет область D(0) и претендентом на эту область (отрезок) – область (отрезок), к которой направлена штриховка.
Пример. Пусть дано характеристическое уравнение САР в виде:
![]() (2.30)
(2.30)
где
![]() - заданные постоянные времени;
- заданные постоянные времени;
![]() -
общий
коэффициент усиления.
-
общий
коэффициент усиления.
САР состоит из трех апериодических звеньев первого порядка. Необходимо определить значения , при котором система устойчива.
Построим границу D-разбиения в плоскости комплексного параметра и будем иметь в виду лишь разбиение действительной оси, т.е. действительные значения .
Граница D-разбиения соответствует уравнению
![]() (2.31)
(2.31)
Г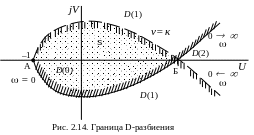 раница
D-разбиения
согласно выражению (2.31) представлена
на рис. 2.14.
раница
D-разбиения
согласно выражению (2.31) представлена
на рис. 2.14.
Претендентом на область устойчивости является область S, к которой направлена штриховка границы D-разбиения. Можно показать, что эта область является не только претендентом, но и самой областью устойчивости. Действительно, точка (0, 0), т.е. =0 лежащая в области S, принадлежит области устойчивости D(0), ибо при =0 характеристическое уравнение (2.30) превращается в уравнение
![]()
все три корня
![]()
которого
лежат в левой полуплоскости. Значит САР
устойчива, если действительные значения
изменяются
в пределах, определяемых отрезком АБ.
Предельное значение
определяется точкой Б. Система устойчива
и при отрицательных значениях
(отрицательные значения
могут
быть при положительной обратной связи).
Для нахождения
![]() (точка Б) следует определить значение
,
при котором V()=0,
где
– предельное значение
,
при котором САР устойчива.
(точка Б) следует определить значение
,
при котором V()=0,
где
– предельное значение
,
при котором САР устойчива.
Пусть корень уравнения V()=0 отличен от нуля ( =0), тогда =U(0). Опуская промежуточные вычисления, из уравнения (2.31) получим
![]()
где
![]()
На рис. 2.14 показаны области D(0), D(1) и D(2). Область D(3) в данном случае отсутствует. Это означает, что при положительных значениях Т1, Т2 и любом значении невозможно, чтобы все три корня уравнения (2.30) находились в правой полуплоскости.
