36,Дивергенция и ротор магнитного поля

Для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие

Эта формула выражает теорему Гаусса для вектора В: поток вектора магнитной индукции через любую за­мкнутую поверхность равен нулю.

Заменив в соответствии с (1.110) поверхностный ин­теграл в (6.98) объемным, получим, что

Условие, к которому мы пришли, должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если подынтегральная функция в ка­ждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его дивергенция всюду равна 0:

Теперь обратимся к циркуляции вектора В. По опреде­лению циркуляция равна интегралу

Проще всего вычислить этот интеграл в случае поля пря­мого тока. Пусть замкнутый контур лежит в плоскости, перпендикулярной к току (рис. 6.25; ток перпендикулярен к плоскости чертежа и направлен за чертеж). В каждой

В каждой точке контура вектор В направлен по касательной к окружности, проходящей через эту точку. Заменим в выражении для циркуляции ВdL на Вlp [dl_B — проекция эле­мента контура на направление вектора В). Из рисунка видно, что dl_B равно bd, где b — расстояние от провода с током до dI ( d — угол, на который поворачивается ра­диальная прямая при перемещении вдоль контура на от­резок dl. Таким образом, подставив выражение (6.25) для В, получим

С учетом равенства (6.101) имеем

При обходе по контуру, охватывающему ток, радиальная прямая все время поворачивается в одном направлении, поэтому §da = 2. Иначе обстоит дело, если ток не охва­тывается контуром (рис. 6.25 б). В этом случае при обходе по контуру радиальная прямая поворачивается сначала в одном направлении (участок 1-2}, а затем в противопо­ложном (участок 2-1), вследствие чего d равен нулю. Учтя этот результат, можно написать

где под I следует подразумевать ток, охватываемый конту­ром. Если контур тока не охватывает, циркуляция вектора В равна нулю.

Знак выражения (6.103) зависит от направления обхода по контуру (в этом же направлении отсчитывается угол ). Если направление обхода образует с направление тока правовинтовую систему, величина (6.103) положительна, в противном случае — отрицательна. Знак можно учесть, полагая I алгебраической величиной, причем положитель­ным нужно считать ток, направление которого связано с направлением обхода по контуру правилом правого винта;

ток противоположного направления будет отрицательным.

С помощью соотношения (6.103) легко восстановить в памяти формулу (6.30) для В поля прямого тока. Пред­ставим себе плоский контур в виде окружности радиуса R (рис. 6.26). В каждой точке этого контура вектор В оди­наков по модулю и направлен по касательной к окружно­сти. Следовательно, циркуляция равна произведению В

на длину окружности 2b, и соотношение (6.103) имеет вид

В • 2b = I₀

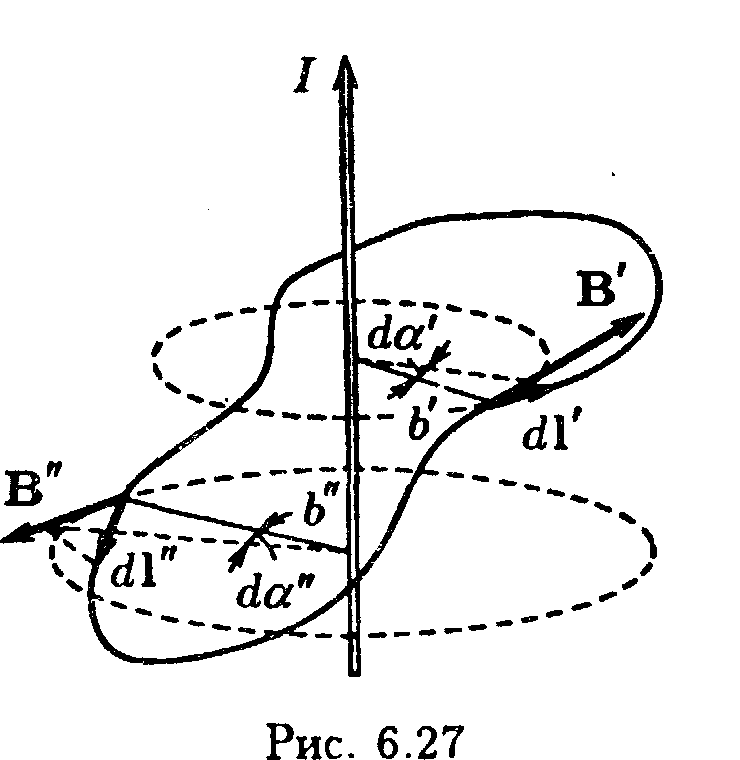
Случай неплоского контура (рис. 6.27) отличается от рассмотренного выше случая плоского контура лишь тем, что при перемещении вдоль контура радиальная прямая не только поворачивается вокруг провода, но и перемеща­ется вдоль него. Все выкладки, приведшие нас к формуле (6.103), остаются справедливыми, если под d подразу­мевать угол, на который поворачивается проекция ради­альной прямой на перпендикулярную к току плоскость.

Суммарный угол поворота этой проекции равен 2, если контур охватывает ток, и ну­лю в противном случае. Сле­довательно, мы снова при­ходим к формуле (6.103).

Формула (6.103) получена нами для случая прямого тока. Можно показать, что она справедлива и для тока, текущего по проводу произвольной формы, например для кругового тока. Допустим, что некоторый контур охва­тывает несколько проводов с токами. В силу принципа суперпозиции (см. (6.16))

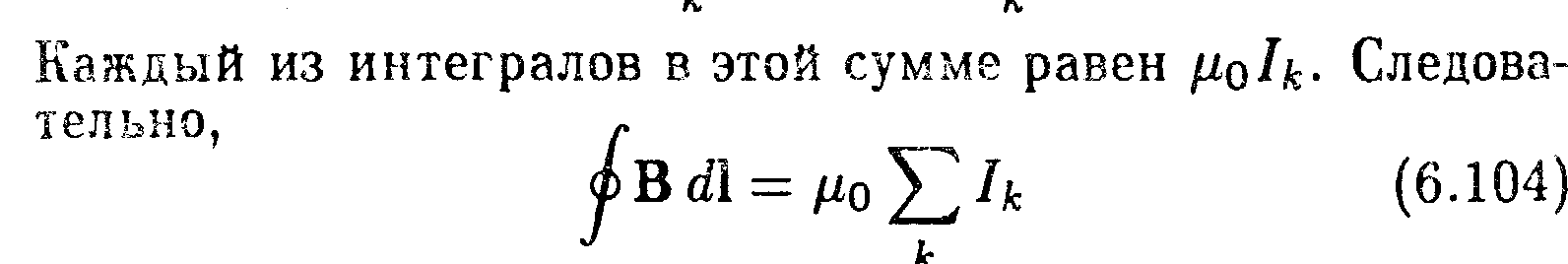
Если токи текут во всем пространстве, где расположен контур, алгебраическую сумму токов, охватываемых контуром, можно представить в виде

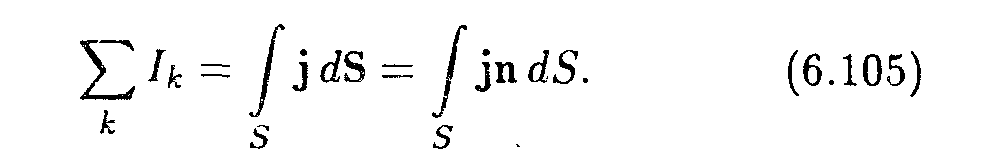
Интеграл берется по произвольной поверхности S, натяну­той на контур. Вектор j есть плотность тока в той точке, где расположена площадка dS; n — положительная нор­маль к этой площадке (т. е. нормаль, образующая с напра­влением обхода по контуру при вычислении циркуляции правовинтовую систему). Заменив в (6.104) сумму токов выражением (6.105), получим Bdl = o _sjdS. Преобра­зовав левую часть по теореме Стокса, придем к равенству

Полученное равенство должно выполняться при произволь­ном выборе поверхности S, по которой берутся интегралы. Это возможно лишь в том случае, если подынтегральные функции имеют в каждой точке одинаковые значения. Та­ким образом, мы приходим к выводу, что ротор вектора магнитной индукции пропорционален вектору плотности тока в данной точке:

Коэффициент пропорциональности в СИ равен о.

Отметим, что формулы (6.104) и (6.106) справедливы только для поля в вакууме в отсутствие меняющихся во времени электрических полей.

Итак, мы нашли дивергенцию и ротор магнитного поля в вакууме. Сравним полученные формулы с аналогичными формулами для электростатического поля в вакууме. Со­гласно (1.119), (1.114), (6.99) и (6.106)

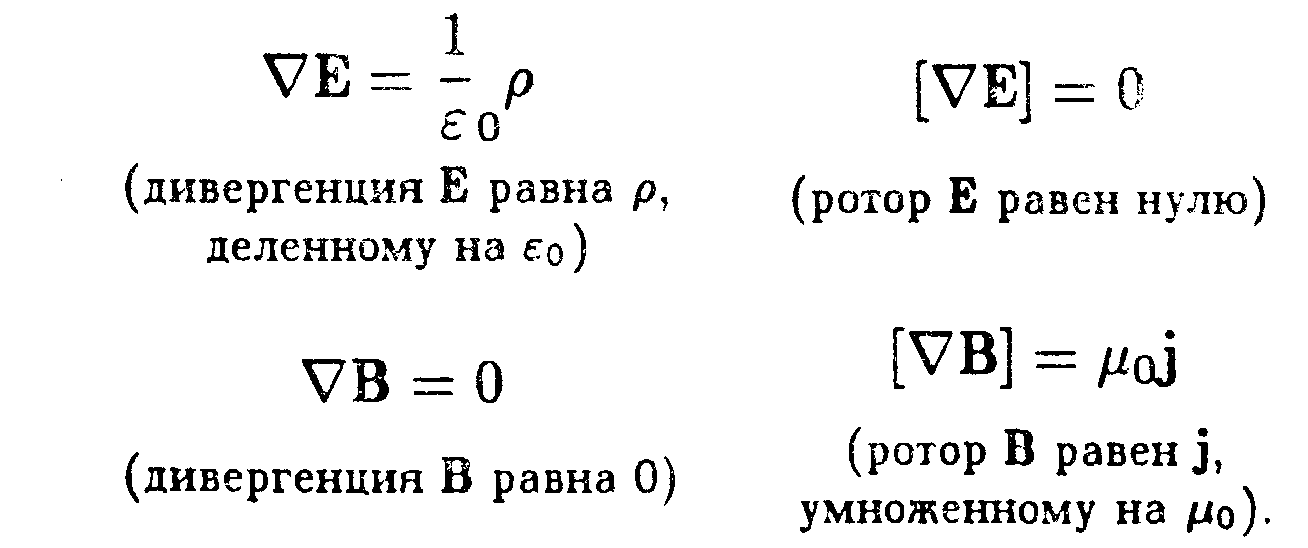
Сопоставление этих формул показывает, что электро­статическое и магнитное поля имеют существенно раз­личный характер. Ротор электростатического поля равен нулю; следовательно, электростатическое поле потенци­ально и может быть охарактеризовано скалярным потен­циалом . Ротор магнитного поля в тех точках, где есть ток, отличен от нуля. Соответственно циркуляция вектора В пропорциональна току, охватываемому контуром. По­этому магнитному полю нельзя приписать скалярный по­тенциал, который был бы связан с В соотношением, ана­логичным (1.40). Этот потенциал не был бы однознач­ным — при каждом обходе по контуру и возвращении в ис­ходную точку и получал бы приращение, равное ₀l. Поле, , у которого ротор отличен от нуля, называется вихревым или соленоидальным.

Поскольку дивергенция вектора В всюду равна нулю, этот вектор можно представить в виде ротора некоторой функции А:

Функция А называется векторным потенциалом магнитного поля.