37, Поле соленоида и тороида

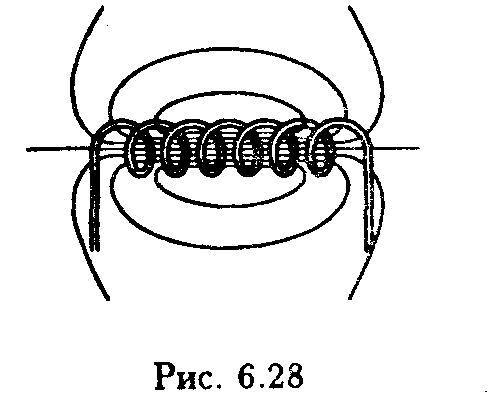
Соленоид представляет собой провод, навитый на круг­лый цилиндрический каркас. Линии В поля соленоида вы­глядят примерно так, как показано на рис. 6.28. Внутри соленоида направление этих линий образует с направле­нием тока в витках правовинтовую систему.

У реального соленоида имеется составляющая тока вдоль оси. Кроме того, линейная плотность тока j_лин (рав­ная отношению силы тока dI к элементу длины соленоида dl} изменяется периодически при перемещении вдоль со­леноида. Среднее значение этой плотности равно

где п — число витков соленоида, приходящееся на еди­ницу его длины, / — сила тока в соленоиде.

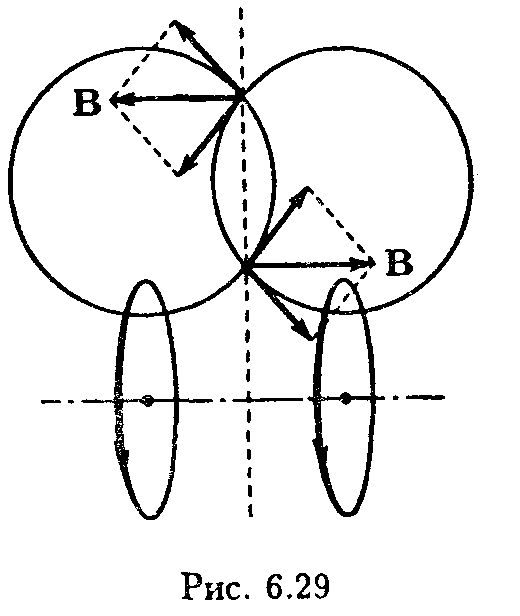
Представим соленоид в виде бесконечного тонкостенного цилиндра, обтекаемого током постоянной линейной плотности

Разобьем цилиндр на одинаковые круговые токи — «вит­ки». Из рис. 6.29 видно, что каждая пара витков, располо­женных симметрично относительно некоторой плоскости, перпендикулярной к оси соленоида, создает в любой точке этой плоскости магнитную индукцию, параллельную оси. Следовательно, и результирующее поле в любой точке вну­три и вне бесконечного соленоида может иметь лишь на­правление, параллельное оси.

Из рис. 6.28 вытекает, что направления поля внутри и вне конечного соленоида противоположны. При увеличе­нии длины соленоида направления полей не изменяются и в пределе при l со остаются противоположными. Для бесконечного соленоида, как и для конечного, направление поля внутри соленоида образует с направлением обтекания Цилиндра током правовинтовую систему.

Из параллельности вектора В оси вытекает, что поле как внутри, так и вне бесконечного соленоида должно быть однородным. Чтобы доказать это, возьмем внутри соленоида воображаемый прямоугольный контур 1-2-3-4 (рис. 6.30; участок 4-1 идет по оси соленоида). Обойдя контур по часовой стрелке, получим для циркуляции век­тора В значение (B₂ – В₁}. Контур не охватывает то­ков, поэтому циркуляция должна быть равна нулю . Отсюда следует, что B₁ = В₂. Располагая участок контура 2-3 на любом расстоянии от оси, мы ка­ждый раз будем получать, что магнитная индукция В₂ на

этом расстоянии равна индук­ции B₁ на оси соленоида. Та­ким образом, однородность по­ля внутри соленоида доказана.

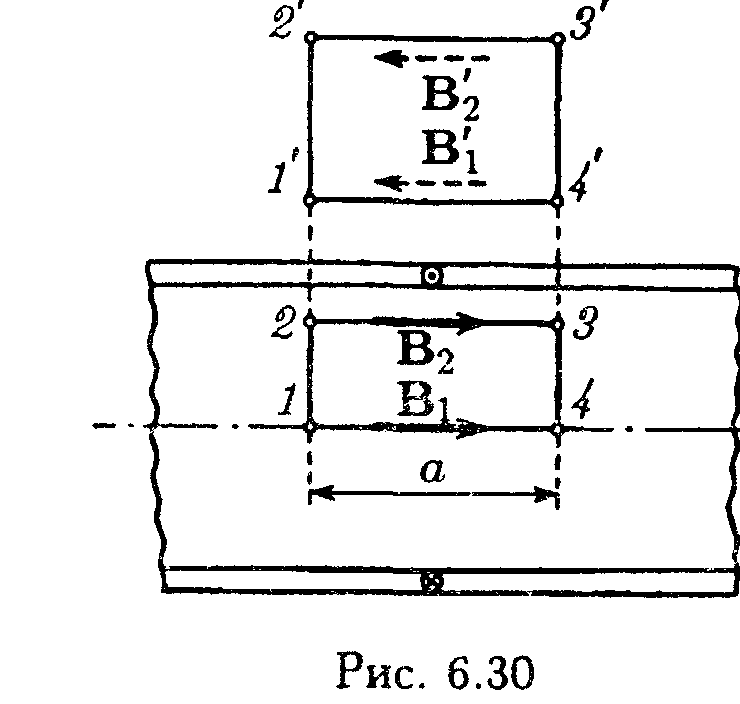
Теперь обратимся к контуру 1'-2'-3'-4¹ • Мы изобра­зили векторы В₁ и В'₂ штриховой линией, поскольку, как выяснится в дальнейшем, поле вне бесконечного солено­ида равно нулю. Пока же мы знаем лишь, что возмож­ное направление поля вне соленоида противоположно на­правлению поля внутри соленоида. Контур 1'-2'-3'-4' не охватывает токов; поэтому циркуляция вектора B^/ по этому контуру, равная [В₁ —В₂], должна быть равна нулю. От­сюда вытекает, что В₁= В₂. Расстояния от оси соленоида до участков 1'-4' и 2'-3' были взяты произвольно. Следо­вательно, значение В на любом расстоянии от оси будет вне соленоида одно и то же. Таким образом, оказывается доказанной и однородность поля вне соленоида.

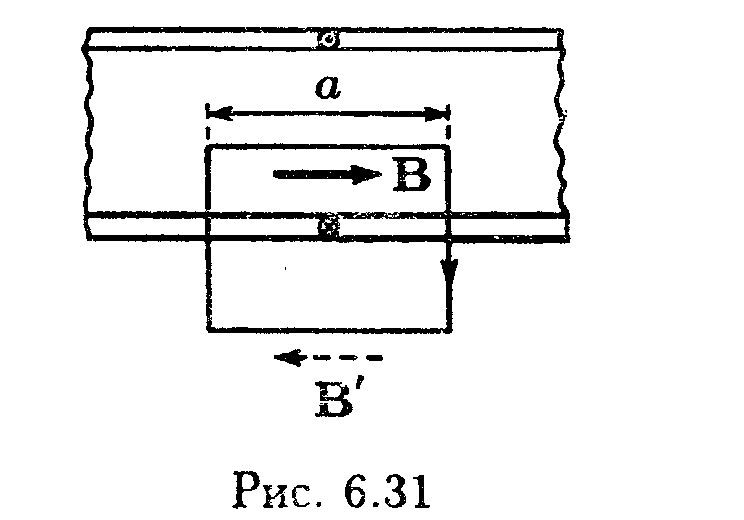
Циркуляция по контуру, изображенному на рис. 6.31, равна а(В+-В') (для обхода по часовой стрелке). Этот кон­тур охватывает положительный ток j_лина. В соответствии с (6.104) должно выполняться равенство

или после сокращения на а и замены j_дин на п1

Из этого равенства следует, что поле как внутри, так и снаружи бесконечного соленоида является конечным.

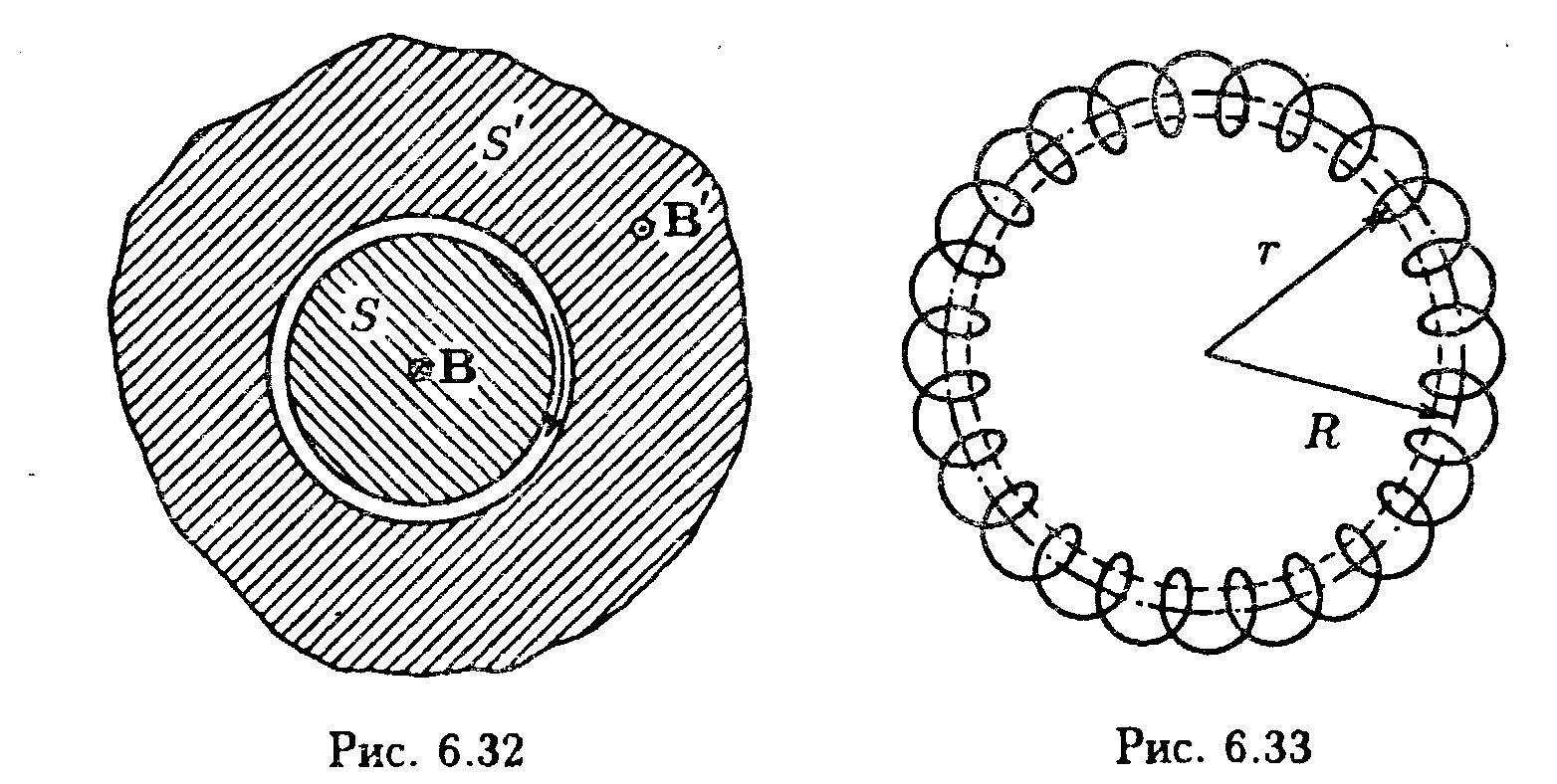
Возьмем плоскость, перпендикулярную к оси солено­ида (рис. 6.32). Вследствие замкнутости линий В магнитные потоки через внутреннюю часть S этой плоскости и через внешнюю часть S' должны быть одинаковыми. По­скольку поля однородны и перпендикулярны к плоскости, каждый из потоков равен произведению соответствующей магнитной индукции и площади, пронизываемой потоком. Таким образом. получается соотношение

Левая часть этого равенства конечна, множитель S¹ в пра­вой части бесконечно большой. Следовательно, В' == 0.

Итак, мы доказали, что вне бесконечно длинного соле­ноида магнитная индукция равна нулю. Внутри солено­ида поле однородно. Положив в (6.110) В' = 0, придем к Формуле для магнитной индукции внутри соленоида:

Произведение п1 называется числом ампер-витков на метр.

В магнитную индукцию на оси соленоида симметрично Расположенные витки вносят одинаковый вклад . Поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине значения (6.Ill):

Практически, если длина соленоида значительно боль­ше, чем его диаметр, формула (6.111) будет справедлива для точек в средней части соленоида, а формула (6.112) — для точек на оси вблизи его концов.

Тороид представляет собой провод, навитый на кар­кас, имеющий форму тора (рис. 6.33). Возьмем контур в виде окружности радиуса r, центр которой совпадает с центром тороида. В силу симметрии вектор В в каждой точке должен быть направлен по касательной к контуру. Следовательно, циркуляция В равна

(В — магнитная индукция в тех точках, где проходит кон­тур). Если контур проходит внутри тороида, он охваты­вает ток 2Rп1 (R — радиус тороида, п — число витков на единицу его длины). В этом случае

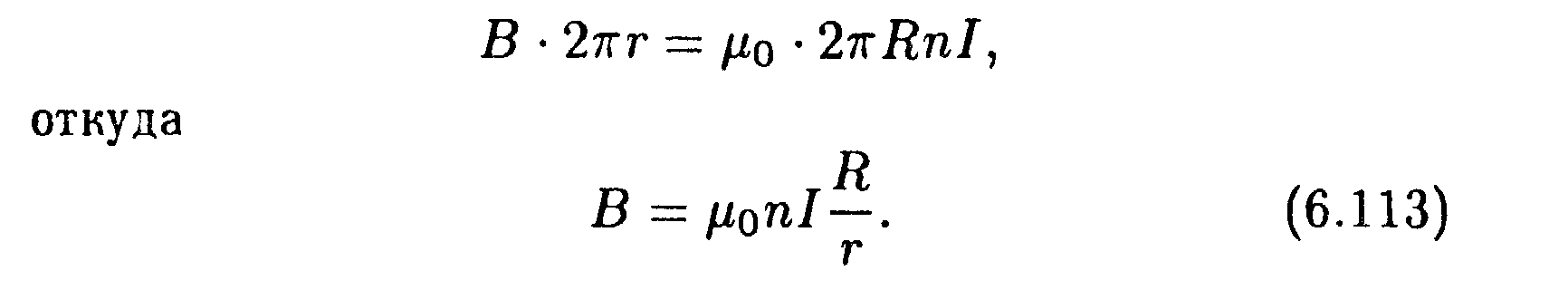
Контур, проходящий вне тороида, токов не охватывает, поэтому для него В •2r = 0. Таким образом, вне тороида магнитная индукция равна нулю.

Для тороида, радиус которого R значительно превос­ходит радиус витка, отношение R/г для всех точек вну­три тороида мало отличается от единицы и вместо (6.113) получается формула, совпадающая с формулой (6.111) для бесконечно длинного соленоида. В этом случае поле можно считать однородным в каждом из сечений тороида. В раз­ных сечениях поле имеет различное направление, поэтому говорить об однородности поля в пределах его тороида можно только условно, имея в виду одинаковость моду­ля В.

У реального тороида имеется составляющая тока вдоль оси. Эта составляющая создает в дополнение к полю (6.113) поле, аналогичное полю кругового тока.