КР+ДР+MAPLE (2) 15 КАНТ-2005

ОТЧЕТНОСТИ ЗА ВТОРОЙ СЕМЕСТР

(инструкция по выполнению)

ФИТ , группы АП-21 и АП-22

Контрольная работа на неопределенные интегралы (2 семестр)

1. Найти общее решение уравнения с разделяющимися переменными (преподавателям – о стационарном решении даже не упоминать!)

.

а) Заменяем y’ на dy/dx. Получаем .

б) Разделяем переменные (игреки – налево, иксы – направо) по правилу: «множители переносятся наискосок». Получаем .

в) Интегрируем полученное равенство. Получаем ответ

.

Примечание. В этом примере используется правило линейной подстановки:

Если , то. Множитель называется поправкой интегрирования.

2. В втором примере применяют метод подведения под знак дифференциала. Используется одна из формул:

xdx=(1/2)d(x²), e^xdx=d(e^x), (1/x)dx=d(lnx), sinxdx= – d(cosx), cosxdx=d(sinx) .

Пример. .

3. В 3-м примере производят замену переменной по правилу: а) При наличии квадратного трехчлена ax²+bx+c делают замену x=t–b/(2a) , б) При наличии корня из линейной функции этот корень принимают за t.

Далее необходимо по функции x(t) найти dx=x’(t)dt и всё это подставить в подынтегральное выражение. Проинтегрировав полученное выражение, следует вернуться с старой переменной х.

Пример.

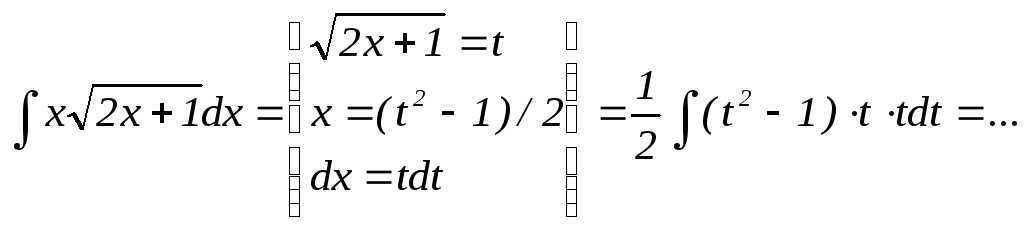
4. В 4-м примере следует произвести интегрирование по частям. Для этого подынтегральное выражение разбиваем на два множителя u и dv. При помощи дифференцирования находим du ,а при помощи интегрирования находим v. Затем применяем формулу .Указание. За и принимаем множитель при Sin(.. ) , Cos(.. ) , e^{(.. )} . При наличии lnx за и принимаем этот логарифм.

5. В последнем примере нужно проинтегрировать рациональную дробь. Если эта дробь неправильная, то при помощи деления «уголком» её превращают в сумму многочлена и правильной дроби. Для интегрирования правильной дроби с простыми корнями в знаменателе следует разложить знаменатель на линейные множители и найти асимптотики правильной дроби в особых точках (метод «затыкания» и подстановки). Правильная дробь будет равна сумме этих асимптотик. Интеграл от каждой из асимптотик – это натуральный логарифм.

Контрольная работа

НА

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

с бесконечными пределами (2 семестр)

(решаются первый и последний примеры)

1. Вычисление несобственного интеграла 1 рода по определению.

а) Бесконечный предел заменяем параметром А.

б) Вычисляем получившийся определенный интеграл.

в) Находим предел полученного выражения при А   .

Если этот предел существует и не равен бесконечности, то говорят, что интеграл сходится, и его значение равно значению этого предела. Если же предел не существует либо равен бесконечности, то говорят, что интеграл расходится. При вычислении предела следует использовать соотношения:

⁽⁺⁾= , ^(–)=0 , ехр(+)= , ехр(–)=0 , ln()= , arctg(+)=/2 .

Пример. . Вывод: Несобственный интеграл сходится и равен ½ .

2. Применение предельной теоремы сравнения. Подынтегральную функцию заменяем функцией, эквивалентной данной функции при х  . Для этого используем соотношения эквивалентности, формулы Маклорена для функций e^x , sinx , cosx , ln(1+x) ,(1+x)ⁿ , а также правило сохранения главных слагаемых. Получившийся упрощенный несобственный интеграл исследуем на сходимость по определению. Делаем вывод о сходимости исходного интеграла.

Пример. . Рассмотрим подынтегральную функцию и используем соотношение эквивалентности.

. Интеграл расходится по определению. Следовательно, исходный интеграл также расходится по теореме сравнения..