Фуккциям многих переменных. (2 семестр)

ЗАДАЧА № 1. Нахождение области определения функции сводится к решению неравенств с двумя неизвестными.

Разобрать на примере аналог метода интервалов

ПРИМЕР. Решить неравенство.

Решение.а) Определяем ОДЗ – пунктирная (запрещенная) гипербола. б) Неравенство превращаем в равенство и строим соответствующую линию (сплошную, т.к. неравенство нестрогое). в) Вся плоскость разделилась линиями пунктов а) и б) на шесть областей. При помощи пробных точек выбираем из этих областей нужные и отмечаем их штриховкой.

Получающаяся картинка является ответом.

Далее следует выяснить характеристики области определения:

замкнутость= граница принадлежит области определения;

ограничен­ность= область определения можно поместить в некоторый круг;

связность= любые две точки области определения можно соединить линией, не выходя за границы области определения.

Примечание. Областьюназывается связное открытое множество.Область определения функциине всегда являетсяобластью.

ЗАДАЧА № 1 решается вручную. MAPLE можно использовать, если есть желание, для построения кривых пунктов а) и б).

ЗАДАЧА № 2. Линия уровня z=C функцииz=f(x,y) это линия, определяемая уравнением f(x,y)=C. В каждой из точек линии уровня функцияz=f(x,y) принимает одно и то же значениеz=C. Две линии различного уровня не могут пересекаться, т.к. в точке пересечения функцияz=f(x,y) принимала бы два различных значения.

Задача №2 выполняется вручную.

ЗАДАЧА № 3 решается при помощи MAPLE. Рассказать о команде

plot3d(f(x,y),x=a..b,y=m..n); и о команде

plot3d({f(x,y),g(x,y)},x=a..b,y=y1(x)..y2(x)); где функцииy1(x) иy2(x) находятся из равенстваf(x,y)=g(x,y).

Рассказать, что картинку можно покрутить правой мышкой.

Пример. Построить объем, ограниченный поверхностями z=x²+y² , z=2–x

Приравниваем функции и находим . Затем применяем команду

> plot3d({x^2+y^2,2-x},x=-2..1,y=-sqrt(2-x-x^2)..sqrt(2-x-x^2));

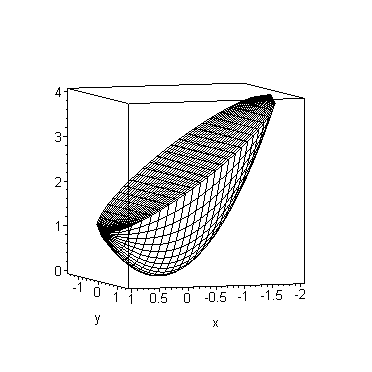
Кстати, отдельно взятый параболоид получится более красивым, если обрезать его по оси Zопцией view=0..4

> plot3d(x^2+y^2,x=-2..2,y=-2..2,view=0..4);

Но лучше всего поверхности вращения строить при помощи параметрических уравнений.

Пусть в плоскости ZOYзадана кривая z=f(y) , y[a, b], которая вращается вокруг оси Z. Тогда эту поверхность вращения можно изобразить командой

> plot3d([u*cos(v),u*sin(v),f(u)],u=a..b,v=0..2*Pi);

Вертикальные цилиндры с уравнением y=f(x) , x[a, b] ,и с протяженностью по z[m, n]можно изобразить командой

> plot3d([х,f(х),z],x=a..b,z=m..n);

Рассказать о совмещении на одном чертеже нескольких объектов при помощи команды >display({A,B,C}); , которая работает с подгрузкой with(plots):

ЗАДАЧА № 5. Решается полностью при помощи MAPLE .

ЗАДАЧА № 6 . Заменив приращение дифференциалом, вычислить

z =

Основное значение z==5 . Найдем дифференциал функции

> z:=sqrt(x^2+y^2);

> dz:=diff(z,x)*dx+diff(z,y)*dy;

> evalf(subs(x=3,y=4,dx=0.007,dy=-0.005,dz));

Ответ: z=5,0002

Найдем точное значение функции

> sqrt(3.007^2+3.995^2);

ЗАДАЧА 7. Экстремум функции многих переменных.

Задаем функцию

> z:=x^3+3*x*y^2-3*x;

_{Находим критические точки}

> solve({diff(z,x),diff(z,y)},{x,y});

_{В данной критической точке вычисляем вторые производные и определитель }

> x0:=-1:y0:=0:

>A:=subs(x=x0,y=y0,diff(z,x,x));B:=subs(x=x0,y=y0,diff(z,x,y));C:=subs(x=x0,y=y0,diff(z,y,y));

> d:=A*C-B^2;

> if d<0 then print ('net*extr') elif d>0 and A>0 then print ('minimum') elif d>0 and A<0 then print ('maximum') end if;

Находим Z_max = subs(x=x0,y=y0,z);

На плоскости XOYнарисовать кривую z=0 . Для этого следует разложить функ­цию на «простенькие» множители х и х²+3у²–3 (иначе MAPLE’у будет тяжело) и затем применить команды

>with(plots):

>implicitplot({x,x^2+3*y^2-3},x=-2..2,

y=-2..2,thickness=3,color=black);

Отметить области z>0 , z<0 и нанести критические точки. Убедиться, что точки максимума соответствуют «холмам», а точки минимума – «впадинам». Объяснить, почему прочие критические точки не являются точками экстремума (рассмотреть знак функции в окрестностях этих точек).

ДОМАШНЯЯ РАБОТА ПО ДВОЙНЫМ ИНТЕГРАЛАМ

Задача. Определить координаты центра тяжести области из домашней работы по определенным интегралам, задача № 2.

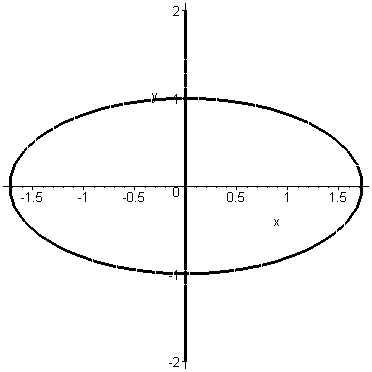
Решение. Пусть Sобласть ограничена линиями у=, у=х–х²/4 , у=4 – х .

1. Строим кривые, находим точки пересечения и выясняем, что область Sможно определить неравенствами , гдеf1(x) , f2(x) – нижняя и верхняя границы области, определяемые командами

> f1:=x->x-x^2/4; f2:=x->piecewise(x<=2,sqrt(2*x),4-x);

Для контроля полезно построить область S (на этот рисунок мы будем в дальнейшем наносить центр тяжести).

> plot({f1(x),f2(x)},x=0..4,color=black);

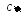
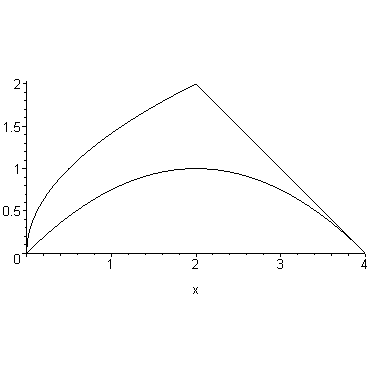
2. Определяем площадь области по формуле . Этот двойной интеграл следует ВРУЧНУЮ свести к повторному, и только затем вычислить при помощи MAPLE

> S:=int(int(1,y=f1(x)..f2(x)),x=0..4);

S:=2

3. Определяем иксовую координату центра тяжести фигуры S:.Этот двойной интеграл следует свести к повторному вручную , а затем вычислить при помощи MAPLE

> Xc:=1/S*int(int(x,y=f1(x)..f2(x)),x=0..4);

4. Аналогичным образом находим вторую координату центра тяжести

> Yc:=1/S*int(int(y,y=f1(x)..f2(x)),x=0..4);

5. Отметить центр тяжести на фигуре S.

Предупреждение. Для выпуклых фигур центр тяжести должен находится внутри области S!!!

6. Аналогичным образом (расписать вручную, вычислить при помощи MAPLE)следует вычислить при помощи двойного интеграла ОБЪЕМ усеченной призмы из домашней работы по определенным интегралам, задача № 3.

7. Вычислить ВРУЧНУЮ двойные интегралы

по площади S этого треугольника АВС. Точки А, В, С взять из последней задачи домашней работы на функциональные ряды.

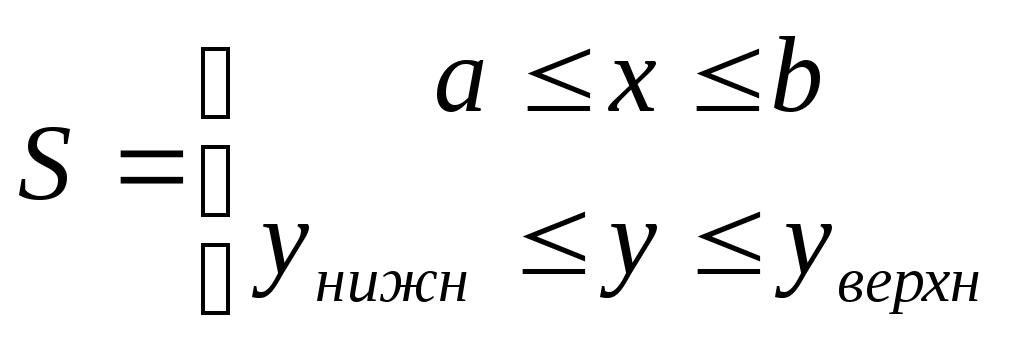Решение. Пишем уравнения прямых по двум точкам: . Затем записываем область треугольника в видеи соответственно этой записи превращаем двойной интеграл в повторный.