Линейная алгебра

Загрузка пакета >with(linalg):

Задание вектора

1) координатами >a: =vector([2,3,4]);a: = [2,3,4]

2) некоторыми первыми координатами с указанием размерности вектора

>b: = vector(4,[2,3]); b: = [2, 3, b3, b4]

Незаданные координаты b3 ,b4 можно в дальнейшем вычислять или задавать

>b[3]:=2^3+4:b[4]:=2^5–1:

>print(b); вывести на экран векторb[2, 3, 12, 31] .

3) Задание нулевого вектора >a:=vector(5,0);a:=[0,0,0,0,0].

4) Задание координат как функций от номера >a:=vector(3,x–>f(x));a:=[f(1),f(2),f(3)].

(аргумент функции можно обозначать любой буквой).

Функцию можно задавать заранее:

>f:=n–>n^3;

>b:=vector(4, f); b:=[1, 8, 27, 64]

или

>h:=n–>diff(x^5, x$n);

>u:=vector(3, h); u:=[5x⁴, 20x³, 60x²] .

Примечание. n -ю координату вектора «а» можно вывести на экран командой >a[n];

Полностью любой вектор «а» выводится на экран командой >print(a);

Задание матрицы.

1) строками >A:=matrix([[1,2,3],[4,5,6]]); .

2) задать число строк (= 3) и число столбцов (= 2), а затем в квадратных скобках записывать через запятую элементы матрицы как строчки в книге

>A:=matrix(3,2,[1,2,3,4,5,6]); .

3) нулевая матрица, содержащая m строк и n столбцов, задается командой >A:=matrix(m,n,0);

4) единичная матрица n n задается командой >Е:=array(1..n,1..n,identity);

5) матрица может быть задана функцией от номера строки mи номера столбцаn

>F:=(m,n)–> 10*m+n:

>A:=matrix(2,3,F); .

Примечание.Для произвольной матрицы А можно вывести на экран командами

>A[m,n]; элементm-й строки иn-го столбца,

>row(A,n); полностьюn-ю строку,

>col(A,n); пполностьюn-й столбец .

Полностью матрица Aвыводится на экран командой >print(A);

Основные задачи линейной алгебры

ВЕКТОРЫ

1) Линейные операции над векторами. >a:=[1,2,3]; >b:=[1,1,1];

>c:=2*a–3*b; Ответ:c:=[–1,1,3]

Линейные операции над векторами a:=vector([1,2,3]); >b:=vector([1,1,1]);

>c:=2*a–3*b; Ответ:c:=2a–3b– отложенная команда

>evalm(c); Ответ: [–1,1,3] – вычисление линейной комбинации.

2) Скалярное произведение двух векторова иb

>dotprod(a,b);

Здесь векторы могут задаваться в форме >b:=[b1,b2,b3] , без словаvector.

3) Нахождение угла между векторами а иb

>angle(a,b);

Здесь векторы могут задаваться в форме >b:=[b1,b2,b3] , без словаvector.

4) Векторное произведение двух векторов а иb

>crossprod(a,b);

Здесь векторы могут задаваться в форме >b:=[b1,b2,b3] , без словаvector.

5) Нахождение базиса для произвольной системы векторов {a,b,c,d}

>basis({a,b,c,d});

6) Ортогонализация системы {a,b,c,d} линейно независимых векторов

>GramSchmidt({a,b,c,d}); [e1,e2,e3,e4] – система ортогональных векторов.

7) Норма вектора и его нормализация (координаты вектора делятся на его длину)

>a:=[3, 4];a:=[3, 4] задание вектора (можно без словаvector)

>norm(a,2); 5 – норма (длина) вектора

>normalize(a); нормализация вектора, ответ: [3/5 , 4/5] .

МАТРИЦЫ

1) Линейная комбинация заданных матриц А и В

>evalm(2*A–3*B); Примечание: А+5 вычисляется как А+5*Е

Умножение матриц подходящих размеров

>evalm(A&*B);

Деление на невырожденную матрицу (умножение справа на А^–1)

>evalm(A/B); Примечание: команда >evalm(1/B); вычисляет В^–1.

Рекомендация. Удобно сначала провести все выкладки с матрицами без команды оценивания, а затем выполнить команду оценивания >evalm(…); Например:

>(2*A+3)&*B/C;

>evalm(%);

2) Вычисление определителя квадратной матрицы А >det(A);

3) Транспонирование матрицы А >transpose(A);

4) Для данной квадратной матрицы А вычисляется присоединенная матрица В (т.е. транспо­нированная матрица из алгебраических дополнений)

>B:=adj(A);

5) Вычисление обратной матрицы для квадратной матрицы А , если det(A)0

>inverse(A);

6) Элементарное преобразование матрицы A: поменять местамиm-ю и n-ю строки

>swaprow(A,m,n);

Аналогичная операция со столбцами осуществляется командой >swapcol(A,m,n);

7) Элементарное преобразование матрицы A: Умножениеn-го столбца на числох

>mulcol(A,n,x);

Аналогичная операция со строкой производится командой >mulrow(A,n,x);

8) Элементарное преобразование матрицы A: столбец с номеромm умножается на числох и прибавляется к столбцу с номеромn

>addcol(A, m, n, x);

Аналогичную операцию со строками производит команда >addrow(A,m,n,x);

9) В матрице А выбирается ненулевой элемент A[m,n] и во всех строках над ним и под ним делаются нули при помощи элементарных преобразований

>pivot(A,m,n);

10) Вычеркивание из матрицы А столбцов с номерами от m доn

>delcols(A,m..n);

Если m=n, то удаляется только один столбец. Аналогичная команда для строк имеет вид

>delrows(A,m..n);

11) Приведение матрицы А к ступенчатому виду

>A:=matrix(3,3,[9,8,7,6,5,4,3,2,1]); задание матрицы.

>gausselim(A); (в ответе возможны дроби).

>ffgausselim(A); 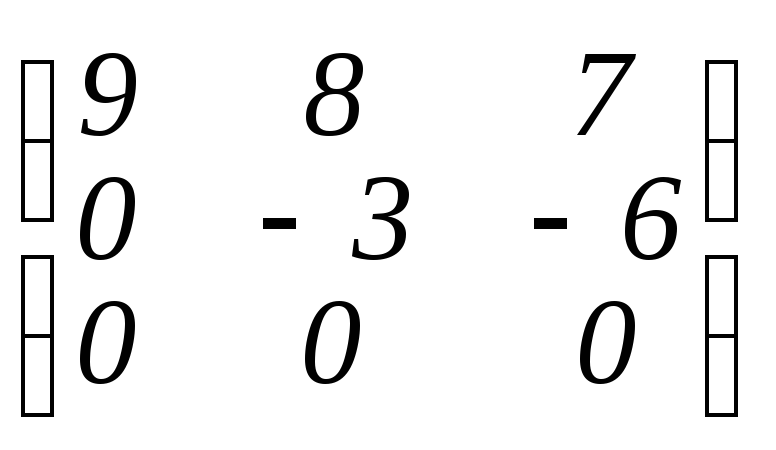(в ответе дроби отсутствуют).

>gaussjord(A); 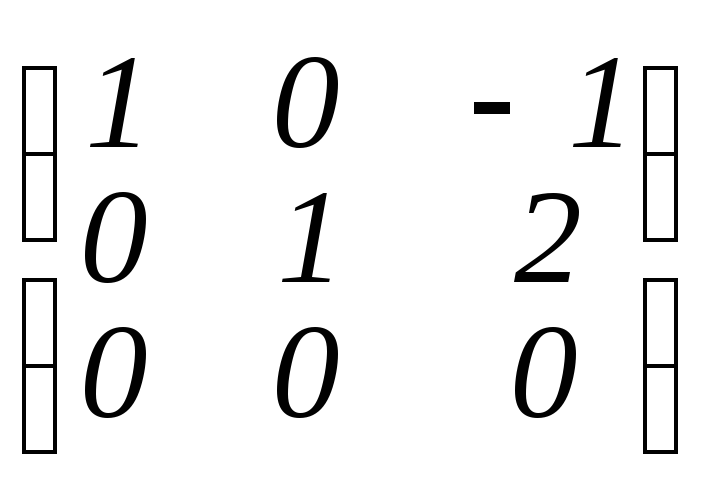приведение матрицы к главному ступенчатому виду.

12) Ранг матрицы А >rank(A);

13) Нахождение характеристического многочлена для квадратной матрицы А

>P:=charpoly(A,lambda); (вместоможно употребить любую другую букву). Команда вычис­ляет характеристический многочлен матрицы А.

Собственные числа матрицы А (корни этого характеристического многочлена) находятся затем командой

>solve(P,lambda);

14) Вычисление собственных значений матрицы А >eigenvals(A);

Ответ записывается в точном виде, если элементы матрицы заданы точно. Если же элементы матрицы заданы в десятичном виде, то собственные значения будут вычисляться приближенно.

15) Вычисление собственных значений (с указанием кратности) и соответствующих собствен­ных векторов

>A:=matrix(2, 2, [5,4,3,9]): задание матрицы А

>eigenvects(A); [3, 1, {[–2, 1]}] , [11, 1, {[1, 3/2]}] .

Здесь 3 – собственное значение , 1 – его кратность, [–2, 1] – собственный вектор.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

1) По данной системе Sсформировать матрицу системы и расширенную матрицу системы

>S:=[2*x+3*y+4*z+5*t=6, x+y+z+t+a, x–y+z–t]; задание системы. Отсутствие знака = означает равенство выражения нулю, квадратные скобки можно заменить фигурными

>V:=[x,y,z,t]; список (list) неизвестных, матрица соответствует порядку неизвестных.

>genmatrix(S,V); матрица системы,

>genmatrix(S,V,flag); расширенная матрица системы.

2) По данной матрице А , неизвестным X:=[…] и правой частиb:=vector([…]); написать однородную или неоднородную систему

>A:=matrix(2,3,[1,2,3,4,5,6]);

>X:=[u,v,w];

>geneqns(A,X); ответ: {u+2v+3w=0 , 4u+5v+6w=0}

>b:=vector([7,8]);

>geneqns(A,x,b); ответ: {4x₁+5x₂+6x₃=8 , x₁+2x₂+3x₃=7}

3)Нахождение общего решения (с параметрами x1,x2,x3, …) для системы линейных уравне­ний с заданной расширенной матрицей Аступенчатоговида

>X:=backsub(A);

Пример.

>A:=matrix(2, 5, [1,2,3,4,10,0,0,1,2,3]);

>X:=backsub(A,false,x); X: = [–2x₂+2x₁+1 , x₂ , –2x₁+3 , x₁].

Для получения какого-нибудь частного решения нужно придать свободным неизвестным (т.е. параметрам x[1] ,x[2]) какие-нибудь значения, например

>x[1]:=1:x[2]:=1: [X[n]$n=1..4}; [1,1,1,1]

4) Решение линейной системы Ax=b(здесь векторbзадается без словаvector)

>linsolve(A,b);

Если система несовместна, то нет никакого ответа. При совместности выдается решение сис­темы в параметрическом виде.

Матричное уравнение АХ=В решается такой же командой >linsolve(A,В);

Для решения матричного уравнения ХА=В нужно решить командой linsolveтранспониро­ванное уравнение А^ТХ^Т=В^Т и затем транспонировать результат. Если матрицы А и В квадрат­ные, то уравнение ХА=В решается командой >X:=evalm(B/A); а уравнение АХ=В решается командой >X:=evalm(1/A&*B);

5) Решение переопределенной системы Ах = bпо методу наименьших квадратов

>A:=matrix(3, 2, [2,3,1,1,1,–1]); задание матрицы А системы уравнений.

>b:=[4,2,3]; задание правых частей векторомb(можно без словаvector),

>leastsqrs(A,b); нахождение решения системы, ответ: [77/30, –2/5].

ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

28) Вычисление ротора векторного поля

>F:=[x*y,y*z,z*x]; задание пространственного векторного поля,

>u:=[x,y,z]; задание переменных, по которым будет вычисляться ротор,

>rotF:=curl(F,u); вычисление ротора, ответ:rotF:=[–y,–z,–x].

29) Вычисление дивергенции векторного поля

>F:=[x*y,y*z,z*x]; задание пространственного векторного поля,

>u:=[x,y,z]; задание переменных, по которым будет вычисляться дивергенция,

>divF:=diverge(F,u); вычисление дивергенции, ответ:divF: =y+z+x

30) Вычисление градиента скалярной функции

>F:=x*y*z; задание скалярной функции,

>V:=[x,y,z]; переменные, по которым будет находится градиент,

>gradF:=grad(F,V); вычисление градиента, ответ:gradF: = [yz,zx,xy].

31) Матрица Вронского от функций f(x),g(x),h(x) находится по команде

>A:=Wronskian([f(x), g(x), h(x)],x);

Определитель Вронского вычисляется затем по команде >det(A);

32) Нахождение потенциала векторного поля.

>f: = [P(x,y),Q(x,y)]; – задание векторного поля,

>potential(f, [x,y],’F’); – проверка поля на потенциальность (true,false) и вычисление

потенциала Fвекторного поляf,

>F; – вывод потенциала на экран.

Аналогичным образом находится потенциал для трехмерного поля.

ЛИНЕЙНЫЕ СТРУКТУРЫ НА ПЛОСКОСТИ

Задание точки.

Точка на плоскости задается двумя координатами в квадратных скобках

>a:=[3, 5];B1:=[–5, 2/3]; и т.д.

Названия точек – это произвольные сочетания букв и цифр. Запрещены названия D,I,O. Вместо них можно писатьd,i,o. Координаты точек должны быть рациональными или десятичными. Запрещены координаты типа,ln(5) . Следует писать в этом случае,ln(5.0).

Точка наносится на плоскость в виде кружочка командой

>PLOT(POINTS(a, B1, [2, 3]), OPTIONS);

где a, В1 – ранее заданные точки, [2, 3] – точка, которая ранее не была определена.

Цвет точки определяется опцией COLOR(HUE,n), где числоп определяется положением на «радужной» шкале

красный оранжевый желтый зелёный голубой синий фиолетовый малиновый

0.0 0.1 0.15 0.3 0.45 0.6 0.8 0.9

Примечание. Можно сначала заранее задать множество точек командой

>W:=POINTS(a,B1, [2, 3]);

а уже затем нанести их на плоскость командой

>PLOT(W);

Ломаная линия.

Ломаная линия задается командой

>P:=CURVES([a,b,c,d]); гдеa,b,c,d– ранее заданные точки.

На плоскость ломаная линия наносится командой

>PLOT(P,OPTIONS);

В качестве опций можно рассматривать толщину линии – THICKNESS(n). Чем большеп, тем больше толщина ломаной. Наряду с опцией цветаCOLOR(HUE,n) можно определять цвет, задавая интенсивности цветов: красного (r), зеленого (g), синего (b) –COLOR(RGB,r,g,b).

Примечание. Можно сразу задать несколько ломаных

>P:=CURVES([a,b,c,d], [p,q,r,s]);

а затем построить их одной командой.

>PLOT(P,OPTIONS);

Многоугольник (замкнутая ломаная линия).

Пусть заданы точки a,b,c,d. Тогда многоугольник, образованный отрезками [a,b], [b,c], [c,d], [d,a] задается командой

>Q:=POLYGONS([a,b,c,d]);

На плоскости этот многоугольник рисуется командой

>PLOT(Q,OPTIONS);

Граница многоугольника рисуется черным цветом, толщина границы задается опцией THICKNESS(n). Опция цвета дает заливку многоугольника этим цветом, границы остаются черными.

Этот же многоугольник можно нарисовать командой

>PLOT(CURVES([a,b,c,d,a]), OPTIONS);

В этом случае опция цвета не дает заливку, а раскрашивает только границу многоугольника.

Примечание. Можно сразу задать несколько многоугольников

>Q:=POLYGONS([a,b,c], [p,q,r,]);

а затем построить их одной командой.

>PLOT(Q,OPTIONS);

Надпись в данной точке.

Текст “KANT” в точке [3, 5] задается командой

>R:=TEXT([3, 5],KANT,OPTIONS);

После этого текст наносится на плоскость командой

PLOT(R);

В качестве опций можно брать опцию цвета надписи, а также опции горизонтального и вертикального выравнивания текста:

ALIGNLEFT,ALIGNRIGHT– надпись слева или справа от точки

ALIGNABOVE,ALIGNBELOW– надпись сверху или снизу от точки.

Опции горизонтального и вертикального выравнивания можно применять одновременно

Совмещение объектов на одном рисунке.

Ранее заданные объекты P,Q,Rсовмещаются на одном рисунке командой

>PLOT(P,Q,R);

ЛИНЕЙНЫЕ СТРУКТУРЫ В ПРОСТРАНСТВЕ

Задание точки.

Точка в пространстве задается тремя координатами в квадратных скобках

>a:=[3, 5, –1];B1:=[–5, 2/3, 0]; и т.д.

Названия точек – это произвольные сочетания букв и цифр. Запрещены названия D,I,O. Вместо них можно писатьd,i,o. Координаты точек должны быть рациональными или десятичными. Запрещены координаты типа,ln(5) . Следует писать в этом случае,ln(5.0).

Отрезки определяются двумя точками.

Множество отрезков задается командой

>P:=CURVES([a,b],[c,d],[e,f]);

Затем эти отрезки строятся в пространстве командой

>PLOT3D(P,OPTIONS);

Многоугольники.

Множество многоугольников определяется командой

>Q:=POLYGONS([a,b,c],[p,q,r]);

Затем эти многоугольники строятся в пространстве командой

>PLOT3D(Q,OPTIONS);

Совмещение объектов на одном рисунке.

PLOT3D(P, Q, OPTIONS);

Задача. Построить плоскостьz=10 – 2x + y над областью {1 ≤ x ≤ 3 , x  y  2x } и сечение её плоскостьюх = 2.

> a:=[1,0,0]:b:=[2,0,0]:c:=[3,0,0]:

a1:=[1,1,0]:b1:=[2,2,0]:c1:=[3,3,0]:

a2:=[1,2,0]:b2:=[2,4,0]:c2:=[3,6,0]:

A1:=[1,1,9]:B1:=[2,2,8]:C1:=[3,3,7]:

A2:=[1,2,10]:B2:=[2,4,10]:C2:=[3,6,10]:o:=[0,0,0]:

> P:=CURVES([o,c1],[o,c2],[a,a2],[b,b2],[c,c2],

[a1,A1],[a2,A2],[c1,C1],[c2,C2]):

> Q:=POLYGONS([A1,A2,C2,C1],[b1,B1,B2,b2]):

> PLOT3D(P,Q,THICKNESS(4),COLOR(RGB,0,0,1));