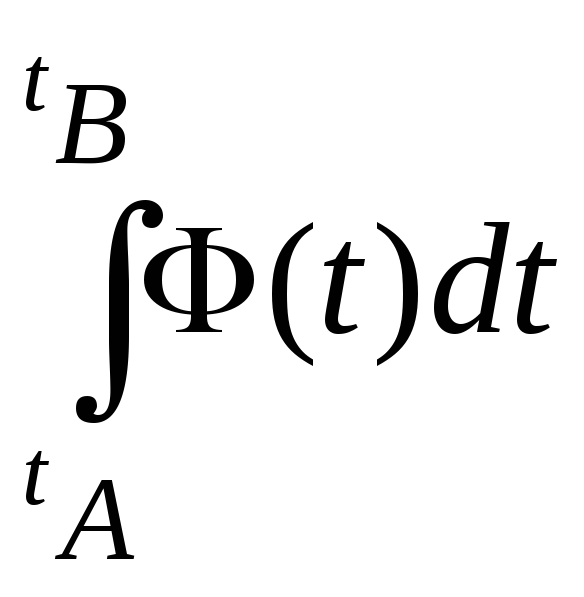№1 Понятие числового ряда и его сходимости. Необходимое условие сходимости

Сумма ряда, или бесконечная сумма, или ряд, — математическое выражение, позволяющее записать бесконечное количество слагаемых и подразумевающее значение их суммы, которое можно получить в предельном смысле. Если значение суммы (в предельном смысле) существует, то говорят, что ряд сходится. В противном случае говорят, что он расходится.

Пустьa1,a2…an… - последовательность чисел. ЧислоSn=a1+a2+….+a3 называется частичной суммой ряда.Сумма ряда– предел частичных суммесли он существует или конечен. Таким образом, если существует числоS= , то в этом случае пишут=S.Необходимое условие сходимости -= 0

Доказательство.Если, то и, но, следовательно .

№2 Признаки сравнения для рядов с положительными членами

Пусть даны два положительных ряда и, для которых, хотя бы начиная с некоторого места , выполняется неравенство.Тогда:если сходится ряд (В), то сходится ряд (А); если расходится ряд (А), то расходится ряд (В).

Другими словами, из сходимости большего ряда следует сходимость меньшего ряда, из расходимости меньшего ряда следует расходимость большего ряда. Сразу отметим, что из расходимости большего ряда, как и из сходимости меньшего ряда, никаких выводов о сходимости второго ряда сделать нельзя.

Доказательствоэтого утверждения непосредственно следует изпризнака сходимости положительных рядов: если сходится больший ряд, то последовательность его частичных сумм ограничена, следовательно, ограничена последовательность частичных сумм меньшего ряда, следовательно, меньший ряд сходится; если расходится меньший ряд, то последовательность его частичных сумм неограничена, следовательно, неограничена последовательность частичных сумм большего ряда, следовательно, больший ряд расходится.

№3 Радикальный признак Коши и признак Даламбера

Признак сходимости Коши (радикальный).Пусть для положительного ряда существует. Тогда

если q<1, то ряд сходится,

если q>1, то ряд расходится,

если q=1, то ряд может и сходиться, и расходиться.

Доказательство.1. Пусть<1. Возьмём . .

Если q<1, то число . Итак, при . Прогрессия сходится, так какр<1, поэтому сходится, поэтому сходится.

2. Пусть >1. Возьмём . .

Если q>1, то число . Итак, при . Прогрессия расходится, так какр>1, поэтому расходится, поэтому расходится.

3. Чтобы убедиться, что в случае q=1 мы не можем сделать вывод ни о сходимости, ни о расходимости ряда, рассмотрим два примера: и . Первый из этих рядов сходится, второй расходится, но в обоих случаяхq=1

Признак сходимости Даламбера.Пусть для положительного ряда существует. Тогда

если q<1, то ряд сходится,

если q>1, то ряд расходится,

если q=1, то ряд может и сходиться, и расходиться.

№4 Интегральный признак коши. Оценка остатка

Пусть члены положительного числового ряда являются значениями непрерывной монотонно убывающей неотрицательной функциипри натуральных значениях аргумента:Тогда ряди несобственный интегралсходятся или расходятся одновременно.

Доказательство. Обозначим . Согдасно геометрическому смыслу определённого интеграла, это площадь криволинейной трапеции под кривойу=над отрезком [1,n]. Частичная сумма- площадь ступенчатой фигуры, расположенной над криволинейной трапецией. Сумма- площадь ступенчатой фигуры, расположенной под криволинейной трапецией (пунктирная верхняя граница на рисунке). Очевидно, , или . Из этого неравенства, в котором , , - монотонно возрастающие с ростомnпоследовательности, и следуют все утверждения теоремы.

№5 Признак Лейбница сходимости знакопеременного ряда. Оценка остатка

Если

1. Последовательность, составленная из модулей членов знакочередующегося ряда, монотонно убывает, т.е. ;

2. Выполняется необходимый признак сходимости ряда, т.е. ,

то ряд сходится. Его сумма по абсолютной величине не превосходит абсолютную величину первого члена.

Доказательство.Рассмотрим последовательность чётных частичных сумм ряда. Представим эту сумму в виде . Из первого условия теоремы следует, что суммы в круглых скобках неотрицательны, поэтому последовательность монотонно возрастает с ростомn. С другой стороны, , т.е. эта последовательность ограничена сверху величиной . Следовательно . Но для нечётных сумм , так как по второму условию теоремы . Таким образом, частичные суммы имеют предел независимо от их четности или нечётности, т.е. ряд сходится, и его сумма. Знак суммы совпадает со знаком первого члена.

№6 Абсолютно и условно сходящиеся числовые ряды

Определение.Рядназываетсяабсолютно сходящимся, если сходится рядабсолютных величин его членов. Если рядсходится, а рядрасходится, то рядназывается условно сходящимся.

№7 Понятие функционального ряда. Область сходимости. Понятие равномерной сходимости. Признак Вейерштрасса абсолютной и равномерной сходимости функционального ряда. Теоремы о равномерно сходящихся рядах.

Основные определения. Пусть дана бесконечная последовательность функций.

независимой переменнойх, имеющих общую область определенияD. Ряд называется функциональным рядом.

Значение , при котором функциональный ряд сходится, называетсяточкой сходимостифункционального ряда. Множество всех точек сходимости функционального ряда называетсяобластью сходимостиэтого ряда. Область сходимости обозначимG.

Ряд сходится равномернона областиG, если для любого числа существует такое натуральное число , одно и то же для всех точек ,что приn>Nвыполняется неравенство (или, что тоже самое, , где - остаток ряда послеn-го члена).

Признак Вейерштрасса. Рядсходитсяабсолютно и равномерно, если выполнены условия:

1)Числовой ряд сходится.

2)

1)Теорема о непрерывности суммы равномерно сходящегося ряда непрерывных функций. Если члены функционального ряда - непрерывные функции, и этот ряд равномерно сходится на отрезке , то сумма этого ряда непрерывна на .

2)Теорема о почленном интегрировании равномерно сходящегося ряда.Пусть члены функционального ряда непрерывны на отрезке , и ряд равномерно сходится к своей сумме на этом отрезке: . Тогда , т.е. интеграл от суммы ряда равен сумме ряда, составленного из интегралов от членов равномерно сходящегося ряда.

3)Теорема о почленном дифференцировании равномерно сходящегося ряда.Пусть члены сходящегося ряда - дифференцируемые на отрезке функции, и ряд, составленный из производных , равномерно сходится на . Тогда ряд можно почленно дифференцировать, и , т.е. производная суммы ряда равна сумме ряда из производных.

№8 Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенного ряда.

Определение. Степенным рядом называется функциональный ряд вида

где - постоянные (коэффициенты ряда),- фиксированное число (центр сходимости). Степенной ряд имеет по меньшей мере одну точку сходимости - точку.

Теорема Абеля. Если степенной ряд сходится в точке, то

1.он абсолютно сходится в любой точке х, удовлетворяющей неравенству(т.е. находящейся ближе к точке, чем);

2.он сходится равномерно на любом отрезке , целиком лежащем на интервале с центром врадиуса

3.Если этот ряд расходится в точке , то он расходится в любой точкех, удовлетворяющей неравенству(т.е. находящейся дальше от точки,чем).

Доказательство. 1. Из сходимости рядав точкеследует, что его общий членстремится к нулю при; любая последовательность, имеющая предел, ограничена, следовательно, существует числоСтакое, что. Пусть точкахудовлетворяет неравенству, тогда. Оценим член ряда в точкех:

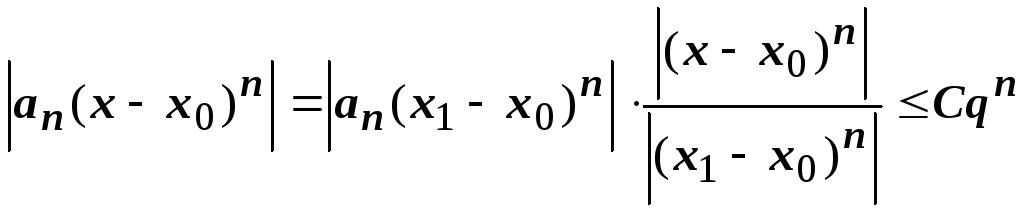. Члены ряда в точкехпо абсолютной величине не превосходят членов сходящейся геометрической прогрессии, следовательно, ряд сходится абсолютно в точкех, следовательно, он сходится абсолютно в любой точке интервала.

2.Пусть отрезок , целиком лежит на интервале. Из точека,bвыберем ту, которая находится дальше от точки, примем для определённости, что это - точкаа: . Тогда для любого х из этого отрезка. В точке ряд, по доказанному, сходится абсолютно, но он является на мажорантой для ряда, следовательно, степенной ряд сходится равномерно на отрезке .

3. Пусть степенной ряд расходится в точке , и. То, что ряд расходится в точкех, докажем от противного. Если предположить, что он сходится в точкех, то, по доказанному, он сходится во всех точках, расположенных ближе к, чемх, следовательно, он сходится в точке, что противоречит условию.

Число Rтакое, что пристепенной ряд сходится, приряд расходится, называетсярадиусом сходимости. Интервалназываетсяинтервалом сходимостистепенного ряда.

№9 Равномерная сходимость степенного ряда. Почленное интегрирование и дифференцирование.

Теорема Абеля. Если степенной ряд сходится в точке, то он сходится равномерно на любом отрезке , целиком лежащем на интервале(т.е. на интервале с центром врадиуса).

Доказательство:Пусть отрезок , целиком лежит на интервале. Из точека,bвыберем ту, которая находится дальше от точки, примем для определённости, что это - точкаа: . Тогда для любого х из этого отрезка. В точке ряд, по доказанному, сходится абсолютно, но он является на мажорантой для ряда, следовательно, степенной ряд сходится равномерно на отрезке .

1 Почленное интегрирование степенного ряда. Пусть сумма степенного ряда на области сходимости равна функции, т.е.. Тогда для

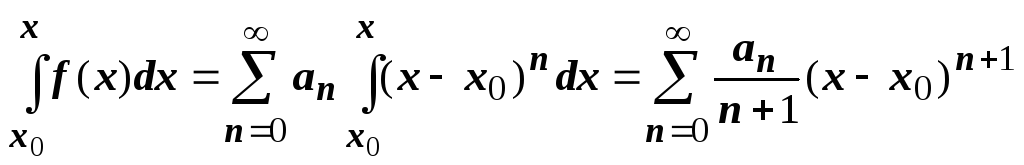
Доказательство.Справедливость этого утверждения следует из равномерной сходимости степенного ряда, составленного из производных членов исходного ряда, на любом отрезке, лежащем в интервале сходимостии о почленном дифференцировании равномерно сходящегося ряда.

2 Почленное дифференцирование степенного ряда. Степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и

Доказательство.Справедливость этого утверждения следует из равномерной сходимости степенного ряда, составленного из производных членов исходного ряда, на любом отрезке, лежащем в интервале сходимости

№10 Понятие ряда Тейлора. Критерий разложимости в ряд Тейлора. Достаточное условие разложимости.

;f(x)=S_n(x)+R_n(x) ;f(x)-S_n(x)=R_n(x) Потребуем, чтобы функцияf(x) имела бесконечное число производныхf⁽ⁿ⁾(x) в точкеx=а и её окрестности. Получим:lim(f(x)-S_n(x))=limR_n(x)=0 (7) . ЕслиlimR_n(x) сущ-ет и равен 0, тоf(x)=limS_n(x) (8) (9) - ряд Тейлора. При а=0 получаем ряд Маклорена.

ЗамечаниеФункция представлена в форме ряда Тейлора в том случае еслиR_n(x)0

Теорема достаточный признак представимости в виде ряда Тейлора

Пусть f⁽ⁿ⁾(x)C=const n=0,1,2... в некоторой замкнутой окрестности точки аХ, тогда функцияfпредставима степенным рядом Тейлора.

№11 Понятие двойного и тройного интегралов. Достаточные условия интегрируемости. Свойства кратных интегралов. Теорема о среднем значении.

Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой

f(x,y) = 0.

Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областьюD. Разобьем областьDнаnчастичных областей сеткой прямых. Получаем, что площадьSделится на элементарные прямоугольники, площади которых равныS_i=Dx_i×Dy_i

В каждой частичной области возьмем произвольную точку Р(х_i,y_i) и составим интегральную сумму

Определение:Если при стремлении к нулю шага разбиения областиDинтегральные суммы имеют конечный предел, то этот предел называетсядвойным интегралом от функцииf(x,y) по областиD.

Определение. Тройным интегралом от функции f(x, y, z) по области Ω называется предел интегральной суммы , если он существует.Тройной интеграл обозначается

Достаточное условие. Любая непрерывная ф-ция на ограниченной замкнутой области интегрируема.

Свойства Двойного интеграла: (Свойства тройного интеграла идентичны)

1)

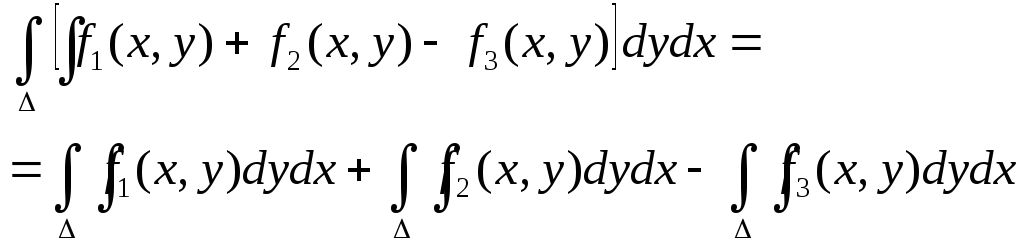
2)

3) Если D=D₁+D₂, то

4) Теорема о среднем. Двойной интеграл от функцииf(x,y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.

5) Если f(x,y)³0 в областиD, то .

6) Если f₁(x,y)£f₂(x,y), то .

7) .

№12 Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.

Замена переменных в двойном интеграле.

Пусть функции взаимно однозначно отображают открытое множество, содержащее областьплоскостина открытое множество, содержащее область, и пустьявляется образом. Еслии их частные производные непрерывны, а определитель

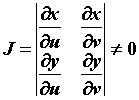, то. Выражениеназывается элементом площади в криволинейных координатах, функциональный определитель- якобианом.

Двойной интеграл в полярных координатах. Введем на плоскости полярные координаты. Пусть- область, полученная взаимно однозначным отображением областиплоскости, определяемым функциями. Тогда, а двойной интеграл в полярных координатах вычисляется по формуле:.Элемент площади в полярных координатах есть.

№13 Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах.

Операция замены переменных в тройном интеграле аналогична соответсвующей операции для двойного интеграла.

Можно записать:

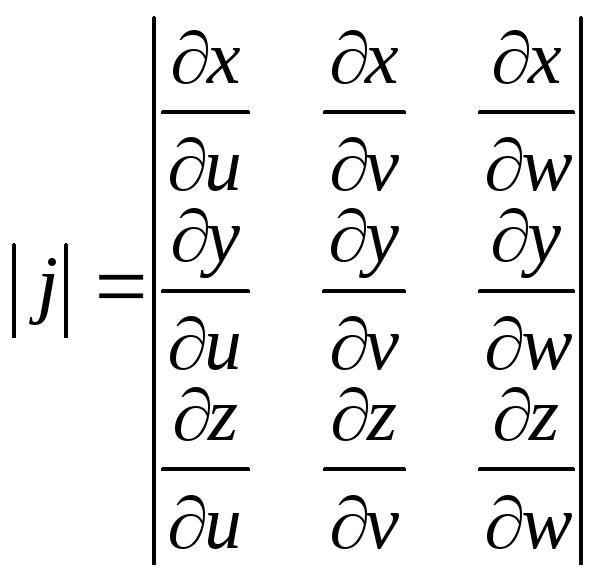
Цилиндрическая система координат.

Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

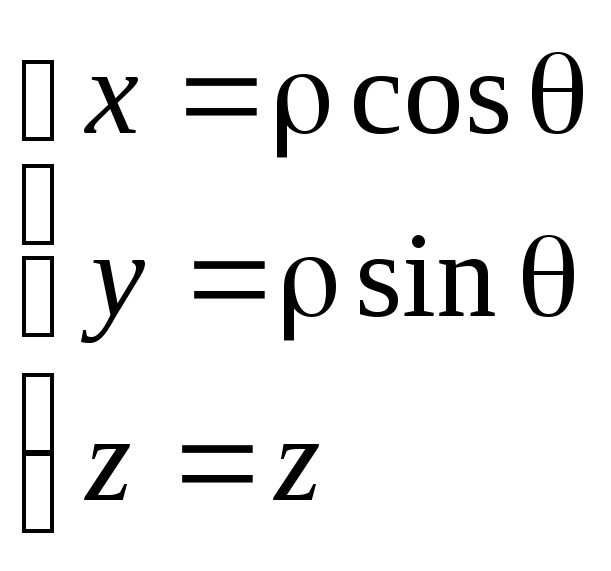
Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан:

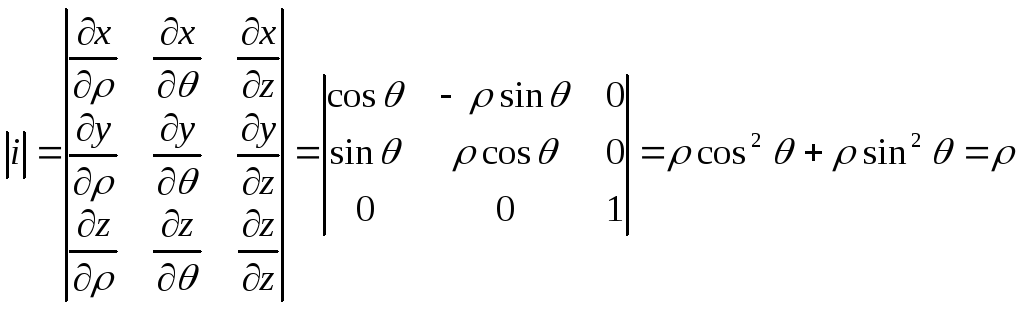
Итого:

Сферическая система координат.

Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

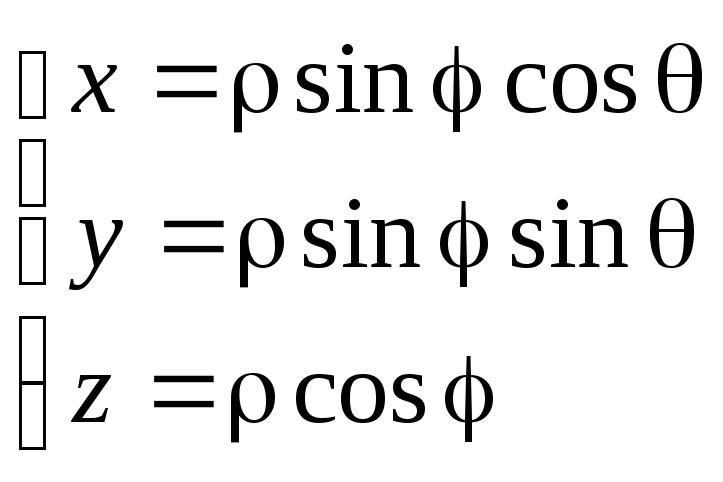
Для представления тройного интеграла в сферических координатах вычисляем Якобиан:

Окончательно получаем:

№14 Площадь поверхности

Рассмотрим кусок поверхности , заданной уравнением. Пусть выполняется условие, что означает, что в каждой точке поверхности существует нормаль с направляющим вектором. Разобьем поверхностьсеткой гладких кривых на элементарные области

( разбиение ). Пусть- наибольший из диаметров элементарных областей. Если независимо от разбиениясуществует, то он и называется площадью данной поверхности. Пустьоднозначно проектируется на плоскостьxoyиG- эта проекция. Элементу площадиобластиGна плоскостиxoyсоответствует элемент площади поверхности, равный:

, где- угол между нормалью к поверхностии осьюOZ. Поэтому вычисление площади поверхности сводится к вычислению двойного интегралапо проекции поверхности на плоскость. Если поверхность задана уравнением, тои площадь поверхности вычисляется по формуле,

здесь - проекция поверхностина плоскостьxoy. Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.

№15 Понятие поверхностного интеграла 1 рода

Пусть некоторая функция определена и ограничена на гладкой поверхности. Выберем разбиениеповерхностии точкина каждой элементарной областии составим интегральную сумму.

Если независимо от выбора разбиения и точексуществует, то он называется поверхностным интегралом по площади поверхности(1-го рода) от функциии обозначается.

 

Билет №16. Скалярное поле. Линии и поверхности уровня. Производная по направлению. Градиент

Если каждой точке Mобластимногомерного пространства поставлено в соответствие некоторое числоu, то говорят, что в этой области заданоскалярное поле.Другими словами, скалярное поле — этофункция, отображающаяRⁿвR

Обычно от скалярной функции требуется непрерывностьилидифференцируемостьдостаточное количество раз (то есть функция должна принадлежатьC^m).

Примеры пространственных скалярных полей: температура.Пример плоского поля: глубина моря, отмеченная каким-либо образом на плоской карте.

Обычно под скалярным полем понимается поле, инвариантное при преобразованиях координат

Поверхность уровня

Скалярное поле можно представить графически с помощью поверхности уровня. Поверхностью уровня скалярного поляu=u(x,y,z) называется множество точек пространства, в которых функцияuпринимает одно и то же значениеc, то есть поверхность уровня определяется уравнениемu(x,y,z) =c.

Для плоского поля вместо поверхности получаются линии уровня. Примеры:изобара,изотермаи прочиеизолинии.

Производная по направлению

В математическом анализе,производная по направлению— это обобщение понятияпроизводнойна случайфункциинескольких переменных. Производная по направлению показывает на сколько быстро функция изменяется при движении вдоль заданного направления.

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производнойпо этой координате. Максимальное значение в точке производная по направлению принимает, если направление совпадает с направлениемградиентафункции в данной точке.

Градиент

Направление скорейшего возрастания поля указываетвекторградиента , или , с координатами:.

Градиент всегда перпендикулярен поверхностям уровня (в плоском поле — линиям уровня). Исключение - особые точки поля, в которых градиент равен нулю.

Билет №17. Поток векторного поля через ориентированную поверхность. Физический смысл. Свойства.

Векторное полехарактеризуется тремя функциямикоторые известным образом преобразуются при поворотах осей координат.

Определение:Векторными линиями поляназываются линии, касательные к которым в каждой точке имеют направление вектора

Определение:Поток вектора  через поверхность S называется скалярная величина, определяемая интегралом

     

Пусть движение несжимаемой жидкости единичной плотности в пространстве задано векторным полем скорости течения v=v(x,y,z). Тогда масса жидкости, которая протечёт за единицу времени через поверхность S, будет равна потоку векторного поля через поверхность S.

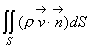
Билет №18. Дивергенция. Формула Остроградского-Гаусса.

Пусть задано векторное поле

 

Определение: 

Дивергенциейилирасходимостью векторного поляназывается скалярная функция, определяемая равенством:

На этот раз векторное поле порождает скалярное поле.

С учетом понятий дивергенции и потока векторного поля (формулу Остроградского) можно представить в форме:

т. е. поток векторного поля через замкнутую поверхность Sв направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.

Билет №19. Понятие криволинейного интеграла второго рода.

Опр: Криволинейным интегралом (2 родапо координатам) от непрерывного векторного поляF(r) вдоль гладкой кривойL : называютчисло

Из определения следует:

Физический смысл:

1) Так как скалярное произведение векторов

F(t)·dr(t)= ||F|| ||dr||cos(F,r), для силового поляFкриволинейный интеграл равен работе по перемещению материальной точки из точкиА в точкуВ по линии L в поле силыF.

Вычисление К.Р.:

2) Алгоритм вычисления криволинейного интеграла :

а) записывается параметрическое уравнение ггладкой линииL

L : r(t) Û x=x(t); y=y(t); z=z(t);

и находятся соответствующие параметрические координаты t_А и t_В точек АиВ;

б) уравнение линии дифференцируется dr(t)=r^'(t)dt=[dx(t);dy(t);dz(t)];

в) записывается векторное поле в точках линии F(t)=[f_X^*(t);f_Y^*(t);f_Z^*(t)]^t;

4) вычисляется скалярное произведение векторов (F(t),dr(t)) и находится явный вид подынтегрального выражения

(f_X^*(t)x’(t)+f_Y^*(t)y’(t)+f_Z^*(t)z’(t))dt=Ф(t)dt;

5) вычисляется определенный интеграл