Свойства решений системы линейных уравнений

 

Если вектор x является решением однородной системыA·x=0, то вектор αx также является решением этой системы. Здесь α — произвольное число.

Если векторы x иy являются решениями однородной системыA·x=0, то векторx +yтакже является решением этой системы.

Если вектор x является решением однородной системыA·x=0, а вектор иy— решение неоднородной системыA·x=b, то векторx +yявляется решением неоднородной системыA·x=b.

Если векторы x иy являются решениями неоднородной системыA·x = b, то векторx −yявляется решением однородной системыA·x=0.

Множество решений однородной линейной системы относительно nнеизвестных являетсялинейным подпространствомпространстваRn.Размерностьэтого подпространства равнаn−r, гдеr−рангматрицы системыA.

КРИТЕРИЙ СОВМЕСТНОСТИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Система линейных алгебраических уравнений совместна тогда и только тогда, когдаранграсширенной матрицы системы равен рангу матрицы системы.

Это утверждение называют теоремой Кронекера-Капелли.

Система линейных алгебраических уравнений

очевидно несовместна.

Ранги расширенной матрицы системы матрицы системы не равны, rank Ap = 2, rankA = 1, rank Ap≠ rankA:

14

Фундаментальная система решений линейного однородного уравнения

 

Определение.Любые линейно независимых решений линейного однородного дифференциального уравнения -ного порядка называетсяфундаментальной системой решенийэтого уравнения.

Из предыдущих теорем сразу следует еще одна важная теорема.

Теорема 7.Решения уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского отличен от 0 хотя бы в одной точке .

Доказательство.Равносильная переформулировка утверждения теоремы – решения линейно зависимы тогда и только тогда, когда на . Но это утверждение сразу следует из теорем 5 и 6.

Теорема 8.Для любого линейного однородного дифференциального уравнения (2) существует фундаментальная система его решений.

Доказательство.Построим такую фундаментальную систему решений. Для этого возьмем произвольную точку и поставим различных задач Коши: .

По теореме 1 о существовании и единственности у каждой из этих задач имеется решение, и мы обозначим - решение 1-й задачи, - решение 2-й задачи, …, - решение -ной задачи. Мы получили - решения уравнения (2). Найдем для этих функций: . Следовательно, по теореме 7, функции образуют искомую фундаментальную систему решений уравнения (2).

Теорема 9.Пусть - фундаментальная система решений уравнения (2). Тогда для любого решения этого уравнения существуют постоянные такие, что .

Доказательство.Возьмем произвольную точку и рассмотрим систему уравнений относительно неизвестных : (11). Определитель этой системы не равен 0, т.к. - фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение . Рассмотрим теперь функцию . По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка включительно в точке совпадают со значениями и ее последовательных производных в точке . По теореме 1 оединственностирешения задачи Коши , .

Замечание.Теоремы 8 и 9 означают, что размерность векторного пространства решений уравнения (2) равна , а любая фундаментальная система решений представляет собой базис этого пространства

15

Система линейных уравнений. Теорема Кронекера-Капелли без доказательства.

Системой линейных алебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

, где чила ,,называются коэффициентами системы, числа - свободными членами. Системы лу удобно записывать в виде матрицы.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если имеет более одного решения. Частным решениемсистемы называется каждое решение неопределённой системы. Общим решением называется совокупность всех частных решений системы. Система лу называется однородной, если все свободные члены равны нулю. Тривиальным называется решение, когда все неизвестные раны нулю.

Теорема: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Теоремы: Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг её основной матрицы был меньше числа неизвестных. Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и лостаточно, чтобы её определитель был равен нулю.

16

Векторы, линейные операции над векторами, их свойства. {определение …}

Вектор – направленный отрезок, который можно передвигать параллельно самому себе.

Два вектора называются равными, если при параллельном переносе, совмещающим начала, совмещаются и концы.

Модулем вектора называется длина вектора (равная корню из суммы квадратов координат). Если модуль вектора равен 1, то вектор единичный.

Два вектора называются коллинеарными, если они лежат на параллельных или совпадающих прямых.

Три вектора называются компланарными, если при их параллельном переносе, совмещающим начала, они оказываются лежащими в одной плоскости.

Углом между двумя векторами называется угол, полученный при параллельном переносе векторов в общее начало.

ω=0– векторы сонаправлены ω= - противонаправлены ω=/2 – перпендикулярны

Суммой двух векторов является вектор идущий из начала первого вектора в конец второго, если конец первого и начало второго совмещены параллельным переносом.

Суммой двух векторов называется вектор, являющийся диагональю в параллелограмме, стороны которого образованны параллельным переносом векторов в общее начало, и исходящий из точки совмещения.

Разностью двух векторов является вектор идущий из конца второго вектора в конец первого, если их начала совмещены параллельным переносом.

Произведением вектора на число называется вектор, коллинеарный данному, длина которого равна произведению длины данного вектора на число. Если число <0, то вектор, полученный произведением данного вектора на число, будет противонаправлен данному вектору.

1 +=+

2 +(+)=(+)+

3 +=

4 –+=

5 *=

6 ()=(),, R

7 (+)=+,  R

8 (+)=+, R

Проекция и координаты вектора {опр., св-ва}

Осью называется прямая с выбранным направлением, началом и единицей длины.

Проекцией точки А на прямую е называется точка А’, в которой пересекается прямая е с плоскостью, перпендикулярной е и проходящей через точку А’.

Проекцией вектора AB на прямую е называется вектор A’B’, где A’ и B’ соответственно проекции точек A и B на прямую е.

Числовая проекция вектора а на прямую е есть длина проекции а на прямую е или произведение длины вектора а на cos угла между вектором а и прямой е.

1) =0 или ω =/2, то пр₂=0

2) 0 0< ω</2, то пр₂>0

3) 0 /2< ω<0, то пр₂<0

свойства проекций

1. пр_e=||*cosω

2. пр₂+пр₂=пр₂(+)

3. пр_е(*)=пр_е

Док-во 3-го св-ва: при >0 имеем пр_е(*)=||*cosω=*||*cosω= пр_е

при <0: пр_е(*)=||*cos(-ω)= -*||*(-cosω)= пр_е

=0 *=пр₂=0 пр₂(*)=

Разложение вектора по ортам координатных осей

, модуль;

Координаты вектора – числовые проекции на координатные оси.

Координаты вектора равны разностям соответствующих координат его конца и начала.

17

Скалярное произведение двух векторов, его свойства. Условия перпендикулярности векторов. Неравенство Буняковского.

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

.

Т.е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Св-ва скалярного произведения:

1.Переместительное Док-во:

а т.к. и=то

2. Сочетательноет.к

3. Распределительное

т.к.

4. Скалярный квадрат вектора равен квадрату его длины , т.к.

5. Если два ненулевых вектора взаимо перепендикулярны, то их скалярное произведение равно нулю (т.к. косинус 90⁰ равен нулю).

Неравенство Буняковского.

или

Скалярное произвкдкние векторов в коорднинатной форме

Пусть заданы два вектора и

найдём скалярное произведение, используя таблицу скалярного произведени векторов :получится .

Скалярное произведение векторов равно сумме произведений их одноимённыйх координат

Векторное произведение двух векторов. Условие коллинеарносити двух векторов. Антикоммутативность векторного произведения. Векторное произведение в координатной форме.

18

Векторным призведением вектора на векторназываестя вектор, который:

1) перпендикулярен векторам и, т.еи

2) имеет длину, численно равную площади параллелонрамма, построенного на векторах икак на сторонах, т.е.

3) векторы ,иобразуют правую тройку.

Два вектора коллинеарны, если их векторное произведение равно нулю.

Вектороное произведение в координатной форме

, если заданы два вектора и

19

Смешанное произведение векторов. Условие компланарности трёх векторов. Смешанное произведение в координатной форме.

Смешанным произведением векторов ,иназывают векторно-скалярное произведение. Смешанное произведение есть число, равное объёму параллелипипеда, построенного этих векторах, взятому с +, если эти вектора образуют правую тройку, и с -, если левую.

Св-ва смешанного произведения:

1) не меняется при циклической перестановке сомножителей, т.е.

2) не меняется при перемене мест знаков векторного и скалярного умножения

3) меняет знак при перемене мест любых двух векторов-сомножителей, т.е.

, ,

4) смешанное произведение ненулевых векторов ,иравно нулю тогда и только тогда, когда они компланарны.

Выражение смешанного произведения черкз коорлинаты:

Смешанное произведение равно определителю третьего порядка, составленному из координат перемножаемых векторов.

20

Уравнение плоскости, проходящей через заданную точку и имеющую заданный нормальный вектор. Общее уравнение плоскости.

Пусть плоскость Q задана в пространстве точкой M₀(x₀,y₀,z₀) и вектором , перпендикулярным этой плоскости. Возьмём на плоскости точкуM(x,y,z) и составим вектор При любом расположении точкиM на плоскоти Q векторы иперендикулярны, поэтому их скалярное произведение рано нулю, т.е

Общее уравнение плоскости:

Геометрическое значение коэффициентов A, B, и С в общкм уравнении плоскости Ах+By+Cz+D=0

Состоит в том что они являются проекциями на координатные оси Ox,Oy, Oz вектораб перпендикулярного этой плоскости.

21

Положение прямой на плоскости может быть задано одним из следующих способов:

• прямая l проходит через точку параллельно вектору

• прямая l проходит через точки и

• прямая l проходит через точку перпендикулярно вектору

• прямая l проходит через точку и составляет с векторомугол α (см. рис. 11.5.1).

1

Рисунок 11.5.1.

Любой вектор параллельный прямойl, называется направляющим вектором этой прямой. Любой вектор перпендикулярный прямойl, называется нормальным вектором прямой. Если взять на прямой какие-либо две фиксированные точки ито векторв частности, будет направляющим вектором прямой

Пусть прямая l задана точкой и направляющим вектором(см. рис. 11.5.2). ПустьM – произвольная точка прямой.

2 Рисунок 11.5.2.

3 Рисунок 11.5.3.

Обозначим ирадиус-векторы точекиM соответственно. Вектор параллелен прямой, и, следовательно, векторутогда и только тогда, когдаM лежит на прямой. Так как то

Переменная t, принимающая различные значения, называется параметром, а уравнение – векторно-параметрическим уравнением прямой.

Если ввести систему координат то уравнение можно записать в виде

где и– координаты точекиM, а – координаты вектораОтсюда следует, что

Эти уравнения называются параметрическими уравнениями прямой.

Пусть итогда из уравнений следует, что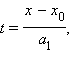и, окончательно, уравнениекоторое называетсяканоническим уравнением прямой, с направляющим вектором

Если то параметрическое уравнение примет вид

Это уравнение задает прямую, параллельную оси Oy и проходящую через точку Каноническое уравнение прямой имеет видАналогично, еслито прямая, задаваемая системой

проходит через точку параллельно осиOx. Ее каноническое уравнение имеет вид

Как было отмечено ранее, направляющим вектором прямой можно выбрать вектор гдеи– произвольные две точки прямой. Тогда, подставив координаты векторав каноническое уравнение, получимуравнение прямой, проходящей через две заданные точки:

Рассмотрим уравнение прямой, проходящей через две точки ипервая из которых лежит на осиOx и имеет, следовательно, координаты а вторая лежит на осиOy и имеет координаты Подставляя их в уравнение, получим

или

Это уравнение называется уравнением прямой в отрезках, так как числа a и b указывают, какие отрезки отсекает прямая на осях координат.

Пусть – некоторая точка прямой,– вектор, перпендикулярный прямой, а– произвольная точка этой прямой (см. рис. 11.5.3). ТогдаM лежит на прямой тогда и только тогда, когда вектор перпендикулярен векторуа для этого необходимо и достаточно, чтобы скалярное произведение векторовиравнялось нулю:Введя радиус-векторыиточекиM, это уравнение можно записать в виде Это –нормальное векторное уравнение прямой, а – нормальный вектор прямой. Если переписать его через координаты точекM и вектор в ортогональной декартовой системе координат, получим

Это уравнение прямой, проходящей через данную точку перпендикулярно векторуОбозначивокончательно имеем

Ax + By + C = 0.

В § 11.4 было показано, что любая прямая может быть задана этим уравнением при условии Назовем это уравнениеобщим уравнением прямой. Следовательно, для любой прямой, заданной общим уравнением Ax + By + C = 0, можно считать, что вектор перпендикулярен прямой, а векторпараллелен ей. Действительно, так каквекторыивзаимно ортогональны, а поскольку– нормальный вектор к прямой, топараллелен ей. Тогда– направляющий вектор прямой.

При рассмотрении векторно-параметрического уравнения прямой мы показали, как перейти к каноническому уравнению, из которого легко получить общее уравнение прямой. Аналогично, из нормального векторного уравнения так же легко перейти к общему уравнению прямой. Покажем теперь, как из общего уравнения прямой получить ее векторные уравнения.

Пусть прямая задана общим уравнением Ax + By + C = 0 в прямоугольной декартовой системе координат. Тогда мы знаем, что вектор – направляющий вектор прямой,– ее нормальный вектор. Так какпредположим для определенности, чтоA ≠ 0. Тогда точка принадлежит прямой. В этом легко убедиться, подставив координаты точки в уравнение прямой. Приведенных данных достаточно, чтобы получить векторные уравнения прямой. Действительно,

– векторно-параметрическое уравнение;

– векторное нормальное уравнение.

23

Понятие о линейном пространстве. Единственность нулевого и противоположного элементов.

Определение. Арифметическим вектором называятся упорядоченная совокупность n чисел. Обозначается , числаназываются компонентами арифметического вектора.

Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: для любых ии любого числа

Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством рифметических векторов­­ Rⁿ.

Вектор называется нулевым вектором, а вектор— противопо

противоположным вектором для вектора .

Для любых ,,изRⁿ и любых чисел α , β справедливо:

1. , сложение коммутативно;

2. ,сложение ассоциативно;

3. 

4. 

5. , умножение на число ассоциативно;

6. ;

7. , умножение на число дистрибутивно относительно сложения элементов;

8. , умножение вектора на число дистрибутивно относительно сложения чисел.

Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме

Линейные подпространства в Rⁿ, размерность подпространства, базис в подпространстве

Определение. Множество L векторов из Rⁿ , такое, что для любых ииз L и любого числа  справедливо , называется линейным подпространством в Rⁿ.

Пример. Множество L арифметических векторов из Rⁿ, у которых последние компоненты — нулевые, образует линейное подпространство в Rⁿ:

Определение. Число k называется размерностью линейного подпространства L, если в L существует система из k линейно независимых векторов, а любые k+1 вектора — линейно зависимы; обозначаем dimL=k.

Определение. Любая линейно независимая система из k векторов k-мерного линейного подпространства L образует базис линейного подпространства L.

Это означает, что если dimL=k и арифметические векторы из L линейно независимы, то для любого существует единственный набор чисел таких, что

24

Примеры линейных пространств.

1). Пространства и,состоящие из всевозможных (упорядоченных) наборов изnчисел (соответственно -- действительных или комплексных). Сложение и умножение определяются формулами

С этими пространствами вы достаточно хорошо знакомы по курсам алгебры и анализа.

2). Непрерывные (действительные или комплексные) функции на некотором отрезке [a,b] с обычными операциями сложения функций и умножения их на числа образуют линейное пространствоC[a,b], являющееся одним из важнейших в анализе и уже встречавшееся вам, например, при изучении функциональных рядов.

3). Пространство быстроубывающих функций ,с которым вы работали, изучая преобразование Фурье.

4). Пространство l₂, в котором элементами служат последовательности чисел (действительных или комплексных)

удовлетворяющие условию

с операциями

является линейным пространством. Тот факт, что сумма двух последовательностей, удовлетворяющих условию (1), также удовлетворяет этому условию, вытекает из элементарного неравенства

Конечный набор элементов линейного пространстваLназываетсялинейно зависимым, а сами элементы --линейно зависимыми, если существуют такие числа,не все равные нулю, что

В противном случае эти элементы называются линейно независимыми. Иными словами, элементыназываются линейно независимыми, если из равенства

вытекает, что .

Бесконечная система элементов пространства Lназываетсялинейно независимой, если любая ее конечная подсистема линейно независима.

Если в пространстве Lможно найтиnлинейно независимых элементов, а любыеn+1 элементов этого пространства линейно зависимы, то говорят, чтоLимеетразмерностьn. Если же вLможно указать систему из произвольного конечного числи линейно независимых элементов, то говорят, что пространствоLбесконечномерно.

Легко понять, что в приведенных выше примерах 2)-4) пространства бесконечномерны, а в примере 1) -- имеют размерность n.

Непустое подмножество L' линейного пространстваLназываетсяподпространством, если оно само образует линейное пространство по отношению к опрелеленным вLоперациям сложения и умножения на число.

Иначе говоря, есть подпространство, если из,следует, чтопри любых числах.

25

Если каждой паре векторов x,yлинейного пространстваLпоставлено в соответствие действительное число(x,y), так, что для любыхx,yиzизLи любого действительного числаαсправедливы следующие аксиомы:

(x, y) = (y, x),

(α·x, y) = α·(x, y),

(x + y, z) =(x, z) + (y, z),

(x, x)> 0 при x ≠ 0, (0, 0) = 0,

то в пространстве L определеноскалярное произведение(x,y).

Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.

Евклидовы пространства EиE' называютсяевклидово изоморфными, если они изоморфны как линейные пространства и если

x∈E,y∈E,x ←→ x' ∈E', y ←→ y' ∈E', то (x, y) = (x', y').

НЕРАВЕНСТВО КОШИ-БУНЯКОВСКОГО

Для любых векторов xиyевклидова пространстваEсо скалярным призведением(x,y)справедливо неравенство:

|(x,y)|²≤(x, x)·(y,y).

Это неравенство называется неравенство Коши-Буняковского.

Иногда это неравенство называют неравенством Шварца.

26

Векторы xиyпространства со скалярным произведениемLназываютсяортогональными, если (x,y)=0. В этом случае пишут.

Процесс ортогонализации Грама--Шмидта позволяет превратить линейно независимую систему векторов в ортонормированную. Вы уже встречались с ним в курсе линейной алгебры. Это обстоятельство позволяет нам сразу перейти к формальному изложению сути дела.

Теорема.Если -- счетная система линейно независимых векторов в линейном пространстве со скалярным произведением L, то новые последовательности

обладают следующими свойствами:

1) система ортонормирована, т. е. любые два ее вектора ортогональны и каждый вектор имеет единичную длину;

2) для любого линейная оболочка векторовсовпадает с линейной оболочкой векторов.

Доказательство.Поскольку норма каждого из векторовz_n, очевидно, равна единице, то для доказательства первого утверждения достаточно убедиться, что (z_m,z_n)=0 при любых.Для этого достаточно проверить, что (y_m,z_n)=0 при любыхn<m.

Так как (y₂,z₁)=(x₂-(x₂,z₁)z₁,z₁)=(x₂,z₁)-(x₂,z₁)(z₁,z₁)= (x₂,z₁)-(x₂,z₁)=0, то наше утверждение верно дляn=1,m=2. Допустим, что оно верно для всех,гдеk-- некоторое натуральное число. Убедимся, что оно верно и для всехn<k+1:

В силу метода математической индукции, первое утверждение теоремы доказано.

Приступая к доказательству второго утверждения теоремы, обозначим через ,линейную оболочку векторов.Поскольку каждый из векторовz₁,z₂,,z_nявляется линейной комбинацией векторов,то, очевидно,.Противоположное включение докажем с помощью индукции. Базой индукции будет очевидное включение.Чтобы сделать шаг индукции, допустим, что для некоторогоkсправедливо включениеи убедимся, что оно же имеет место и для номераk+1. Для этого достаточно проверить, что.Но это непосредственно вытекает из следующей формулы, написанной с учетом предположения индукции:

Теорема доказана.

Для ненулевых векторов xиyевклидова пространства введем понятиеугла, как такого числаиз интервала,для которого выполняется равенство

Ясно, что xиyортогональны если и только если.

27

Линейные операторы. Матрица линейного оператора. Примеры линейных операторов.

Определение. Если каждому элементу ставится в соответствие единственный элемент, то говорят, что в пространствеRⁿ задан оператор, действующий в пространстве Rⁿ.

Результат действия оператора A на элемент обозначают .

Если элементы и связаны соотношением , то называют образом элемента ; элемент — прообразом элемента .

Множество элементов пространства Rⁿ, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A).

Множество элементов пространства Rⁿ, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если , то.

Ядром оператора называется множество элементов пространства Rⁿ, образом которых является нуле

нулевой элемент. Ядро оператора обозначают Ker(A): .

Определение. Оператор A, действующий в пространстве Rⁿ называется линейным оператором, если для любых изRⁿ и для любого числа α справедливо:

и .

Определение. Матрица, столбцами которой являются координаты образов соответствующих базисных векторов некоторого базиса в Rⁿ —

называется матрицей линейного оператора A в данном базисе.

Примеры.

Нулевой оператор: — линейный оператор,D(Θ)= Rⁿ, ,.

28

Образ и ядро линейного оператора

Рассмотрим линейный оператор , действующий в конечномерном линейном пространстве. Доказано, что образлинейного операторалинейное пространство. Размерность образа линейного оператора называетсярангом оператора, обозначается .

Ядром линейного оператора называется множество элементов из , образом которых является нулевой элемент. Ядро оператора обозначают:. Ядро линейного операторалинейное пространство; размерность ядра линейного оператора называетсядефектом оператора, обозначается :.

Для линейного оператора, действующего в n-мерном линейном пространстве , справедливы следующие утверждения:

сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор: ;

ранг оператора равен рангу его матрицы;

ядро оператора совпадает с множеством  решений линейной однородной системы с матрицей , размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;

столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.

Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.

29

Изменение координат вектора при изменении базиса

Пусть в -мерном линейном пространствевыбран базис, который мы будем для удобства называть "старый" и другой базис, который мы будем называть "новый". Возьмем призвольный векториз. Его координатный столбец в старом базисе обозначим, а в новом --. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.