10. Формула трапеций.

Вычисляем площадь крив-й трапеции

Разобьем отрезок [a,b] на n-равноотстоящих узлов.

[x0,x1]… [xn-1,xn] yi=f(xi) Sтр=(a+b)*h/2

Отаточный член ф-лы трапеций.

R=(интеграл от x0 до x1)ydx-h/2 *(y(x0)+y(x1)); R(h)=R(0)+(интегр. от 0 до h )(R’(h)dh=-1/12 *h³ y’’(C1), Cc(x0,x1);R=-1/12 * h³ y’’(C); -распространим этот рез-т на любое число звеньев, т.е. на весь промежут. [a,b].R=∑(от i=1до n)(интегр. от X(i-1) до xi) (ydx-h/2 *(y(i-1)+yi))=h³/12(∑ от i=1 до n )y’’(Ci); Cic(X(i-1);Xi);Рассмотр. среднее арифметич. μ=(∑ от 1 до n)y’’(Ci)/n; Значение μ заключ. м-у наибол. и наименьш. знач-ями 2-ой производной на [a,b] m2<=μ<=M2. А т.к. 2-ая производ. непрер. на [a,b] то она приним. все промежут. знач-я м-у M2 и м2; Т.е. μ=y’’(C)=(∑y’’(c))/n; R=-nh³y’’(c)/12=-h²(b-a)y’’(c)/12; Т.е. данная ф-ла явл. точной только для многочленов первого пор-ка. Иногда быв. неудобно вычисл. 2-ую произв. для вычисл. погрешн-ти, поэт. вычисл. интегр. с шагом h; I_h=∑h+Mh², где М-оценка (-(b-a)y’’(c))/12; Затем вычисл. I_2h=∑2h+M4h²; поэт. оценка может быть выраж. ф-лой R=(∑h- ∑2h)/3.

11. Формула Симпсона.

Число шагов дел-ся на 4 иначе вычислить Σ с шагом 2h невозможно

h=(b-a)/n=(b-a)/2m Через каждые три точки будем проводить параболу y=A0+A1x+A2x2 Чтобы парабола проходила через точки кривой (x0,y0), (x1,y1), (x2,y2) необ-мо подобрать коэф-ты A0, A1, A2 след-м образом

x0=0 x1=h x2=2h соотв-но

/ y0=A0

| y1=A0+A1h+A2h2

\ y2=A0+2A1h+4A2h2

Т.к. значение h и y известны найдём А0 А1 А2

A0=y0 A1=(4y1-y2-3y0)/2h A2=(y0-2y1+y2)/2h2

Площадь первого элемента

Подстав-я значения А0 А1 А2 получим

I1=h(y0+4y1+y2)/3… In= h(yn-2+4yn-1+yn)/3 Поэтому исходный интеграл:

- Формула Симпсона.

Оценка погрешности в формуле Симпсона.

Предполагаем , что ф-я y непр-на и трижды диф-ма, запишем ошибку в виде:

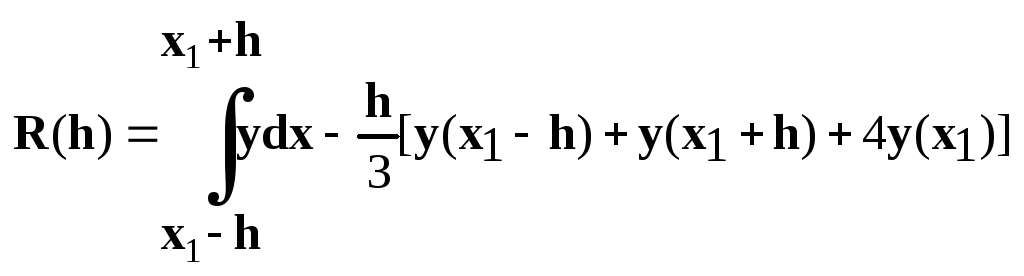
Продиф-м эту ф-ю три раза:

с4(x1-h,x1+h) Проводя аналог-е преобраз-я будем иметь :

- ошибка С1,2,3э(xi-h;xi+h) Ф-ла Симпсона явл-ся точной включая многочлен третей степени.

Суммируем ошибки по всем промежуткам - можно сказать:

При выч-и интеграла как правило польз-ся двойным пересчетом:

Rh=Mh4 R2h=M16h4 R=(h-2h)/15

I=h-(h-2h)/15 - точное значение интеграла.

Для вычисления шага польз-ся формулой e-точность

М4 – наиб знач 4-ой производной.

12. Метод Эйлера решения д.У.

/ y’=f(x,y) В M(xo,y0) проведем касат-ю до

\ y(x0)=y0 пересеч с прям х=х1, получим точку М1. Ч/з точку (x1,f(x1,y1)) проведем касат-ю до пересечения с прямой x=x2 и т.д.

Получится ломанная М0 М1 М2 …

которая заменяет интегральную кривую.

Аналитически этот метод выглядит след-м

образом: Нанесем сетку xi=x0+ih М/у т-ми xi и xi+1 исходное ур-е имеет вид: (yi+1-yi)/h=f(xi,yi).

yi+1=yi+hf(xi,yi) и y0=f(x0) иначе / yi+1=yi+yi

\ yi=hf(xi,yi)

Модиф-й метод Эйлера.

В отличии от метода Эйлера, когда для вычисления след-й точки (xi+1,yi+1) треб-ся информация только о пред-й точке, модиф-й метод предполагает знание о некоторой промежуточной точке: xi+1/2=xi+h/2

Метод закл-ся: yi+1/2=yi+hfi/2

1) Через точку (xi,yi) провод-ся касат-я с

тангенсом наклона tg=f(xi,yi) до пересечения с прямой x=xi+1/2. В полученной точке пересечения по методу Эйлера выч-ся значение ф-ии yi+1/2 и выч-ся новая производная fi+1/2=f(xi+1/2,yi+1/2) Значение этой производной определяет tg второй касат-й, которая провод-ся из получ-й точки.

2)Возр-ся в исходную т. и ч/з неё проводим прямую парал-ю второй касательной yi+1=yi+hfi+1/2

Усовер-й метод Эйлера.

1) Через точку (xi,yi) провод-ся касат-я до пересечения с прямой xi+1=xi+h угловой коэф-т этой прямой tg1=f(xi,yi)

2) В получ-й точке по методу Эйлера выч-ся знач-е ф-ии y”i+1=yi+hf(xi,yi) и выч-ся новая производная tg2=f”(xi+1,y”i+1)

3) Происходит возврат в т. (xi,yi) и ч/з неё провод-ся новая касат-я, где tg есть среднее ариф-е 2х пред-х tg1 tg2.

tg=( tg1+ tg2)/2=( f(xi,yi)+f(xi+1,yi+1))/2

Новое значение yi+1=yi=+h*( f(xi,yi)+f(xi+1,yi+1))/2

Метод Рунге-Кутта. (точность h4, h5)

Точно вычислить значение м-да трудно,т.к. исходя из верного текущего знач-я y(xi) вычис-ют величину y(xi+2h) двумя способами, 1й раз с шагом h, др. раз с 2h. Если расхож-дения значений не превышает допустимой погрешности, то шаг выбран правильно и полученное значение y(xi+2h) М принять за верное, в противоп-м случае шаг умень-ют в 2 раза.

y’=f(x,y) Выб-ся шаг h, и наносится сетка: у(x0)=y0 xi+1=x0+hi Рассмотрим числа:

K1(i)=hf(xi,yi) K2(i)=hf(xi+h/2,yi+ K1(i)/2)

K3(i)=hf(xi+h/2,yi+ K2(i)/2) K4(i)=hf(xi+h,yi+ K3(i))

yi+1=yi+yi шаг yi=(K1(i)+2K2(i)+2K3(i)+K4(i))/6

Удобно на каждом шаге заполнять таблицу:

i	x	y	K=hf(x,y)	y
0	x0	y0	K1(0)	K1(0)
	x0+h/2	y0+к1(0)/2	K2(0)	2K2(0)
	x0+h/2	y0+к2(0)/2	K3(0)	2K3(0)
	x0+h	y0+к3(0)	K4(0)	K4(0)

=(k1+2k2+2k3+k4)/6