§ 2. Интегрирование методом замены переменной и по частям

Метод замены переменной (метод подстановки) – наиболее общий метод, часто применяемый при вычислении интегралов. Им часто приходится пользоваться и для того, чтобы получить табличный интеграл из справочника. Состоит он в том, что при вычислении

(2.1)

вместо переменной хвводится новая переменнаяt по формуле, причемподбирается так, чтобы после подстановки получилась подынтегральная функция, более удобная для интегрирования. При этом справедлива формула

. (2.2)

Для доказательства этой формулы достаточно вычислить дифференциалы от каждой ее части. Имеем

. Дифференциалы равны, поэтому обе части равенства представляют собой одно и то же семейство первообразных для функции, то есть формула (2.2) имеет место.

Таким образом, для вычисления интеграла (2.1) методом замены переменной нужно не только в функции заменитьх на, но ивыразить черезt и, то есть положить. В результате вычисления получим функцию от переменнойt. Чтобы возвратиться к переменнойх, достаточно в полученной функции заменитьtзначением, где– обратная кфункция, то естьt найти из уравнения.

Заметим, что формулу (2.2) часто применяют справа налево, то есть записывают ее в виде

, где. (2.3)

Если – первообразная для функции, то есть, то из (2.3) получаем

.

В частном случае, когда , имеем

откуда

.

Примеры. Вычислим интегралы: 1); 2); 3).

Решение.

1) ==(полагаем=.

2) .

3) .

Выведем теперь формулу интегрирования по частям. Пусть и– функции, дифференцируемые на некотором промежуткеХ. Тогда

,

откуда

.

Интегрируя обе части последнего равенства и учитывая, что для первообразной являетсяuv, получим

. (2.4)

Формула (2.4) и называется формулой интегрирования по частям. Она позволяет свести вычисление интегралак вычислению интеграла, который может оказаться более простым для интегрирования.

Примеры. Вычислим интегралы: 1); 2).

Решение. 1).

2) =.

При вычислении интегралов методом интегрирования по частям важно уметь правильно выбирать u иdv. Общий принцип состоит в том, что получающийся интеграл должен быть проще исходного интеграла.

Укажем некоторые классы интегралов, которые вычисляются методом интегрирования по частям.

I., где– многочлен; нужно положить.

II..

III..

IV.. В каждом из этих интегралов заu берут обратную тригонометрическую функцию.

V.,. Нужно дважды применить формулу интегрирования по частям, оба раза взяв заu либо показательную, либо тригонометрическую функцию.

Пример. Вычислим интеграл.

Решение.. Отсюдаи.

§ 3. Интегрирование рациональных функций

Всегда ли неопределенный интеграл можно выразить через элементарные функции, то есть через степенную, показательную, логарифмическую, тригонометрические и обратные тригонометрические функции с помощью конечного числа арифметических действий и суперпозиций? Производная элементарной функции всегда функция элементарная, для интегралов же это не так. Например, не выражаются через элементарные функции интегралы

и другие.

В дальнейшем нас будут интересовать такие конкретные классы функций, интегралы от которых выражаются через элементарные функции. Самым важным среди таких классов является класс рациональных функций, то есть функций вида , гдеи– многочлены. Интегрирование функций этого класса начнем с рассмотрения простейших случаев.

1) Интегрирование простейших рациональных функций(простых дробей).

Простыми дробями называются дроби следующих четырех типов:

I.;II.;III.;IV., (3.1)

где A,M,N,a,p,q– действительные числа, а квадратный трехчленне имеет действительных корней, так что, откуда.

I., т.е.

, (3.2)

II.,k= 2, 3, …, то есть

. (3.3)

III. Выделим из квадратного трехчленаполный квадрат:

.

Положим (это можно сделать, так как) и. Получим

.

Таким образом,

. (3.4)

IV. Полагая, как и в предыдущем случае,,, получим

. К последнему интегралу, который обозначим, применим формулу интегрирования по частям:

.

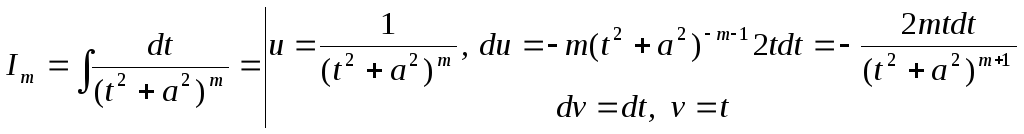
Отсюда получаем рекуррентную формулу для вычисления :

. (3.5)

Поэтому

,

где вычисляется по рекуррентной формуле (3.5),.

Пример 1. Вычислим интеграл.

Решение. Имеем, то есть квадратный трехчлендействительных корней не имеет. Выделим полный квадрат:. Положим. Тогда

.

По формуле (3.5) при иполучим. Поскольку

, имееми

.

2) Интегрирование правильных дробей.

Рациональная дробь называетсяправильной, если степень многочленаменьше степени многочлена(степень числителя меньше степени знаменателя).

Интегрирование правильных дробей основано на следующей теореме, которую мы сформулируем без доказательства (доказательство см., например, в учебнике Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, т.2, гл. VIII, §2, п. 274; возможно доказательство в курсе алгебры):

Теорема. Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых дробей.

Это разложение правильной дроби на простые дроби тесным образом связано с разложением ее знаменателя на простые множители. Из курса алгебры известно, что многочлен с действительными коэффициентами может быть разложен единственным образом на множители 1-ой и 2-ой степени с действительными коэффициентами. Для простоты будем считать, что старший коэффициент многочленаравен 1. Тогда

, (3.6)

где – действительные корни многочлена, а квадратные трехчлены не имеют действительных корней, и

. (3.7)

Показатели у знаменателей последовательно уменьшаются от до 1,,отдо 1, отдо 1,, отдо 1, а– неопределенные коэффициенты. Чтобы найти эти коэффициенты, нужно дроби в правой части равенства (3.7) привести к общему знаменателю, которым, очевидно, будет многочлен, затем знаменатели отбросить. Получим равенство двух многочленов: слева – многочленс известными коэффициентами, справа – многочлен с неизвестными буквенными коэффициентами. Поскольку равенство тождественное относительнох, должны быть равны коэффициенты при одинаковых степеняхх. Приравнивая их, получим систему уравнений относительно неизвестных коэффициентов. Эта система всегда имеет решение на основании сформулированной выше теоремы. Найдя из этой системы неизвестные коэффициенты и подставив их в равенство (3.7), получим разложение правильной дробина сумму простых дробей. Таким образом, интегрирование правильной дробисводится к интегрированию простых дробей в силу равенства (3.7).

Изложенный метод представления правильной дроби в виде суммы простых дробей называется обычно методом неопределенных коэффициентов. Заметим, что неизвестные коэффициенты из равенства многочленов можно находить и иначе, подставляя вместох конкретные значения. При этом тоже будут получаться линейные относительно неизвестных коэффициентов уравнения. В качестве значенийх удобнее всего брать корни знаменателя. При этом почти все члены в правой части равенства обращаются в нуль, что позволяет легко находить оставшиеся коэффициенты. Можно применять также комбинированный способ отыскания неизвестных коэффициентов, при котором уравнения получаются как приравниванием коэффициентов при одинаковых степеняхх, так и подстановкой значенийх.

Пример 2. Вычислим интеграл.

Решение. На основании формулы (3.7) имеем:

,

,

Поэтому.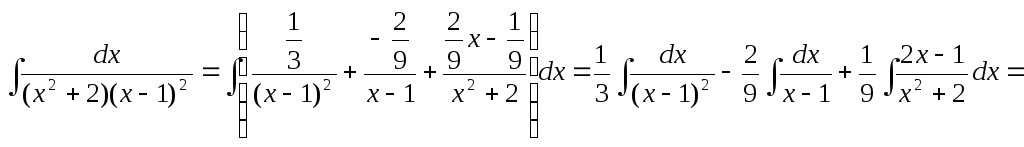

3. Интегрирование рациональных функций.

Пусть – некоторая рациональная функция. Если эта дробь правильная, то интегрировать ее мы уже умеем. Если эта дробь неправильная, то ее можно представить в виде суммы многочлена (целая часть) и правильной дроби, разделивна, как говорят, из этой дроби можно выделить целую часть.

Таким образом, интегрирование неправильной дроби сводится к интегрированию многочлена и правильной дроби. Интегрирование правильной дроби сводится, как мы видели, к интегрированию простых дробей. Интегралы от простых дробей есть функции элементарные – рациональные функции, арктангенсы и логарифмы. Поэтому интеграл от любой рациональной функции выражается через элементарные функции – рациональные функции, арктангенсы и логарифмы.

Пример 3. Вычислим интеграл.

Решение. Рациональная дробь– неправильная, выделим из нее

целую часть:

–

–

х– 2

Таким образом,, причем квадратный трехчлендействительных корней не имеет. Поэтому

.