§ 4. Интегрирование иррациональных функций

В предыдущем параграфе мы установили, что интеграл от любой рациональной функции выражается через элементарные функции. Поэтому в дальнейшем при вычислении интегралов от функций других классов мы будем разыскивать такие подстановки , которые данное подынтегральное выражение преобразуют в рациональное относительно новой переменнойt. Такой прием называетсярационализацией подынтегрального выражения. Вычислив интеграл от полученной рациональной функции и выполнив обратную подстановку, получим выражение первоначального интеграла через элементарные функции.

1. Интегрирование выражений вида .

В дальнейшем условимся буквой R обозначать рациональную функцию своих аргументов. Например,– рациональная функция отх иу. Подставив ввместоувыражение, получим иррациональную функцию отх. Интеграл от нее имеет вид. Этот интеграл сводится к интегралу от рациональной функции с помощью подстановки.

Если под знаком интеграла содержатся корни с разными показателями, но с одним и тем же дробно-линейным относительно хвыражением, то сначала следует привести их к одному показателю, а затем применить указанную выше подстановку. Именно,, гдеm – общий знаменатель дробей.

2. Интегрирование биномиальных дифференциалов.

Дифференциал вида , гдеа иb– любые постоянные, а показателиm,n иp – рациональные числа, называетсябиномиальным дифференциалом. Русский математик П.Л. Чебышев (1821-1894) в 1853 году доказал, что интеграл от биномиального дифференциала вычисляется в элементарных функциях только в следующих трех случаях:

а) когдаp – целое число;

б) когда– целое число;

в) когда– целое число.

Если ни одно из этих условий не выполняется, то интеграл не вычисляется в элементарных функциях.

Случай а) является частным случаем предыдущего пункта. Если– общий знаменатель дробейm иn, то рационализация подынтегрального выражения достигается с помощью подстановки.

В случае б) нужно сделать замену, гдеs – знаменатель дробиp.

В случае в) применяется подстановка, гдеs – знаменатель дробиp.

3. Интегрирование функций вида Подстановки Эйлера.

Интеграл вида рационализируется с помощью одной из трех подстановок Эйлера (1707-1783).

1 – я подстановка Эйлера. Если, то полагаем.

2 – я подстановка Эйлера. Если, то полагаем.

3 – я подстановка Эйлера. Если квадратный трехчленимеет различные действительные корнии, то, считая, получаем

. Поэтому=, то есть получен интеграл, рассмотренный в 1-ом пункте. Подстановка– 3-я подстановка Эйлера.

Примеры. Вычислим интегралы: 1); 2); 3).

Решение. 1) Имеем интеграл, рассмотренный в 3-ем пункте. Поскольку, делаем 2-ю подстановку Эйлера:,,. Поэтому

.

2) Преобразуем подынтегральное выражение: – биномиальный дифференциал с, то естьp – не целое,– не целое,– целое, поэтому делаем 3-ю подстановку Чебышева:и

=.

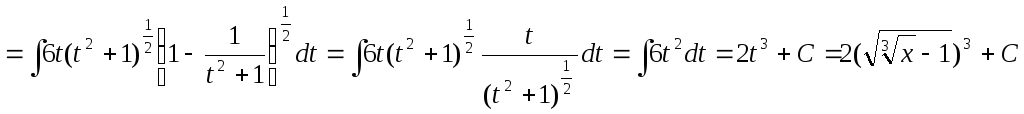3) Подкоренные выражения одинаковы, поэтому можно применить подстановку, рассмотренную в 1-ом пункте. Поскольку общий знаменатель дробей иравен 6, делаем постановку, тогда

.

§ 5. Интегрирование тригонометрических функций

Рассмотрим интегралы вида , гдеR, как и раньше, рациональная функция своих аргументови. Такие интегралы всегда рационализируются с помощью подстановки, которая называетсяуниверсальной подстановкой. Действительно,

,

,,. Поэтому− интеграл от рациональной функции. Следовательно, любой интеграл рассматриваемого вида выражается через элементарные функции.

Пример 1. Вычислим интеграл.

Решение. Имеем

.

Несмотря на то, что универсальная подстановка дает возможность проинтегрировать всякую функцию вида , на практике она часто приводит к слишком громоздким вычислениям. Во многих случаях проще использовать другие подстановки. В частном случае,

если , то,

если , то,

если , тоили.

Эти подстановки предпочтительнее универсальной подстановки, поскольку преобразования получаются менее громоздкими.

Для преобразования подынтегрального выражения часто применяются различные тригонометрические формулы. В первую очередь применяют формулы

,.

Примеры. Вычислим интегралы: 2); 3).

Решение. 2) Преобразуем подынтегральное выражение по одной из приведенных выше формул. Получим=.

3) Подынтегральная функция , поэтому нужно сделать подстановку. Имеем=. Для вычисления последнего интеграла подынтегральную функцию представим в виде суммы простых дробей, воспользовавшись методом неопределенных коэффициентов (подынтегральная функция – правильная рациональная дробь):

,

,

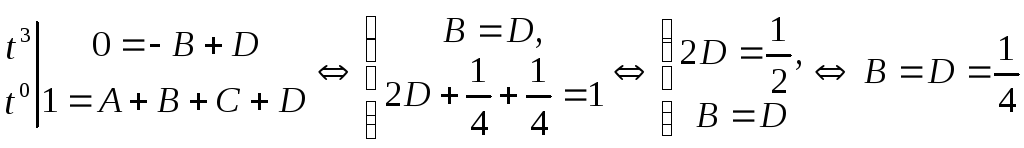. Значит,= =.