9.5 Геометрические и механические приложения криволинейного интеграла по длине дуги

Пусть BC –дуга материальной гладкой кривой, в каждой точке M(x; y; z) которой известна линейная плотность – непрерывная функция точки M(x,y,z). Тогда

_{1) масса дуги BC}

_{2) длина дуги BC}

3) координаты центра тяжести дуги BC

, , ,

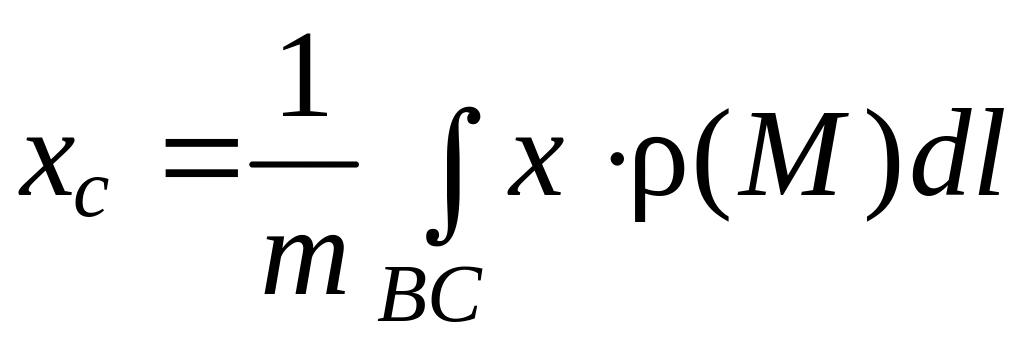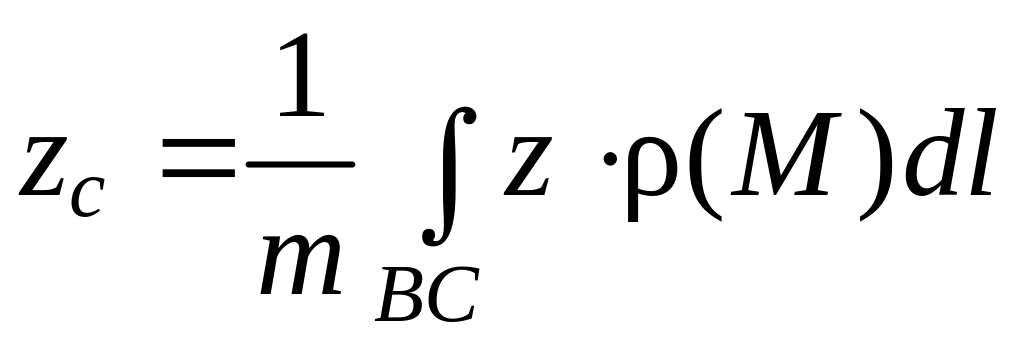( =0 для плоской дуги BC);

4) моменты инерции дуги BC относительно координатных осей Ox, Oy, Oz соответственно:

,

для плоской дуги BС:

Пример. Вычислить криволинейный интеграл:

где BC – первый виток винтовой линии:

Первый виток винтовой линии получим при

На винтовой линии:

Следовательно,

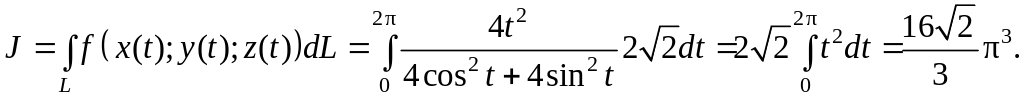Пример. Найти длину l, массу m, координаты x_c , y_c центра тяжести дуги цепной линии между точками с абсциссами x_b = 0 и x_c = a если плотность в каждой точке M(x,y) дуги BC определяется формулой:

На кривой имеем: Следовательно,

;

;

.

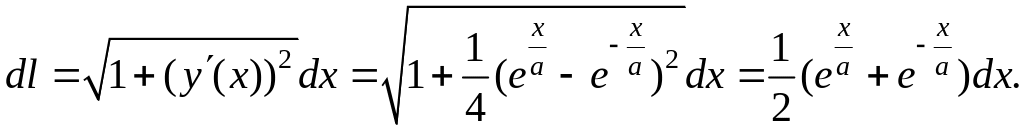
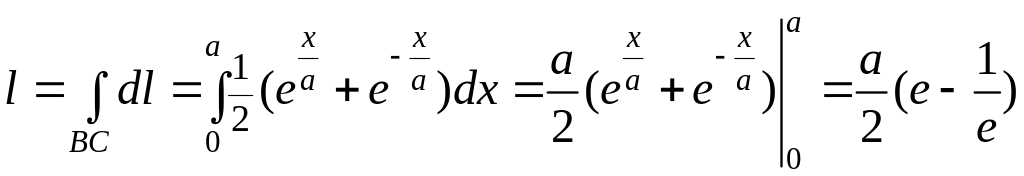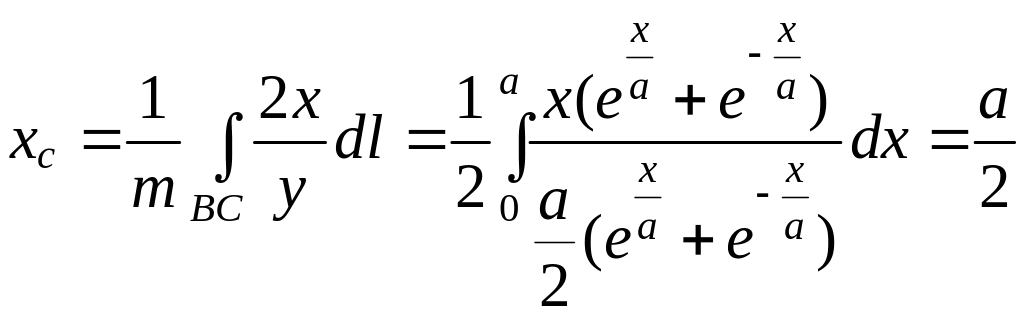
Пример. Найти моменты инерции относительно координатных осей однородного отрезка BC прямой, проходящей через точки B(0; 0; 0) и C(1; 2; 3), .

Параметрические уравнения отрезка BC: x = t, y = 2t, x = 3t, .

На прямой BC имеем: , . Следовательно,

.

;

;

.

9.5 Криволинейный интеграл по координатам

Криволинейный интеграл от непрерывной в некоторой области плоскости функции по координате х вдоль дуги плоской кусочно-гладкой кривой l, расположенной в этой области, связан с криволинейным интегралом по длине дуги соотношением

где  – угол между касательной, проведенной к кривой в любой ее точке, и положительным направлением оси . Аналогично,

,

где  – угол между касательной, проведенной к кривой в любой ее точке, и положительным направлением оси .

Очевидно, что и .

Обычно рассматривают сумму интегралов по координате x и по координате y, которая записывается в виде

.

Криволинейные интегралы по координатам (криволинейные интегралы второго рода) обладают теми же свойствами, что и интегралы по длине дуги. Однако в отличие от последних они зависят от выбора направления обхода кривой: если изменить направление обхода кривой, то интеграл по координатам меняет знак, т. е.

.

При вычислении криволинейного интеграла по длине дуги возможны следующие варианты.

a) Если кривая задана уравнением y = (x) и при перемещении из точки А в точку В аргумент x меняется от a до b, то

.

b) Если кривая задана параметрически: x = (t), y = (t), и при перемещении из точки А в точку В параметр t меняется от  до , то

.

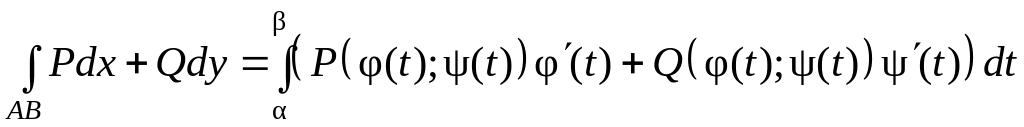В случае замкнутой кривой (точки А и В совпадают) принято направление обхода кривой l выбирать так, чтобы область, ограниченная этой кривой, всегда оставалась слева.

Аналогично определяются криволинейные интегралы по координатам в случае, если кривая l лежит в плоскости (или ) и от непрерывных в некоторой пространственной области функций , , , вдоль дуги пространственной кусочно-гладкой кривой L, расположенной в этой области, т. е.

.

Если кривая задана параметрическими уравнениями (  t  )

, , то

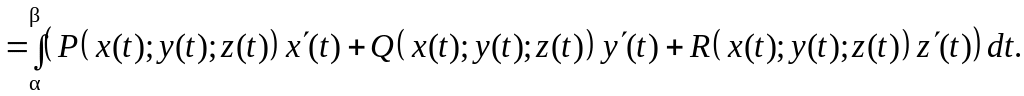
9.6 Формула Грина-Остроградского

Если функции P(x,y) и Q(x,y) и их частные производные и

непрерывны в замкнутой области D , ограниченной кусочно-гладким контуром L , то справедлива формула Грина-Остроградского

.

Символ L+ означает, что контур L обходится в положительном направлении (область D при обходе контура L остаётся слева).