Равносильные формулы логики предикатов

Определение 4.9. Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.

Определение 4.10. Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области.

Здесь, как в алгебре высказываний, для равносильных формул принято обозначение А  В.

Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей. Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание. Тогда

1. ,

2. ,

3. ,

4. ,

5. ,

6. ,

7. ,

8. ,

9. ,

10. ,

11. ,

12. ,

13. ,

14. ,

15. .

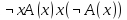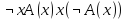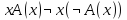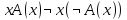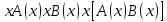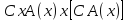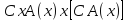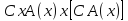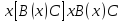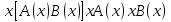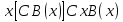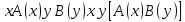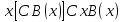Предваренная нормальная форма

Определение 4.11. Говорят, что формула логики предикатов имеет нормальную форму, если она содержит только операции отрицания, конъюнкции, дизъюнкции и кванторные операции.

Используя равносильности алгебры высказываний и логики предикатов, каждую формулу логики предикатов можно привести к нормальной форме.

Среди нормальных форм формул логики предикатов важное значение имеют так называемые предваренные нормальные формы (п.н.ф.). В них кванторные операции либо полностью отсутствуют, либо они используются после всех операций алгебры логики, то есть предваренная нормальная форма формулы логики предикатов имеет вид:

(σх₁)(σх₂)...(σх_п) А(х₁, х₂,..., х_т), п≤т,

где под символом (σx_i) понимается один из кванторов х_i или $х_i, а формула А кванторов не содержит.

Теорема 4.1. Всякая формула логики предикатов может быть приведена к предваренной нормальной форме.

Алгоритм получения предваренной формы для произвольной формулы логики предикатов включает следующие шаги.

1. Исключение связок импликации и эквивалентности.

2. Переименование (если необходимо) связанных переменных таким образом, чтобы никакая переменная не имела бы одновременно свободных и связанных вхождений. Это должно быть выполнено для всех подформул рассматриваемой формулы.

3. Удаление кванторов, область действия которых не содержит вхождений квантифицированной переменной.

4. Сужение области действия отрицаний и снятие двойных отрицаний.

5. Перенос всех кванторов в начало формулы (для этого используются основные равносильности).

Сколемовская форма и сколемизация формул

В формуле, представленной в предваренной нормальной форме, легко добиться, чтобы последними стояли кванторы существования. Для этого используется тождество:

В(х₁,…, z₁,…) ≡ $u[B (х₁,…, z₁,…) Ù I(u)],

где I(и) – произвольная общезначимая формула.

Например, формула имеет вид

$х₁…$х_kу₁…у_m$z₁…$z_р В(х₁,…, х_k, у₁,…, у_m, z₁,…, z_р,…) (*)

Будем теперь «снимать» в формуле (*) последовательно группы кванторов слева направо, заменяя их на функции. Основная идея здесь состоит в том, что пара кванторов u$v – это функция v=f(u). Следовательно, набору кванторов у₁…у_m$z_i отвечает функция z_i = g_i(у₁,…, у_m). Если самой левой группой кванторов являются кванторы существования $х₁…$х_k, то им соответствуют постоянные функции, которые сводятся к заданию их значений a₁,…, a_k.

Сняв группу кванторов в формуле (*), в функции В оставляем переменные у₁,…, у_m, по которым стояли кванторы всеобщности, а вместо следующих за ними переменных z₁,…, z_р, связанных кванторами существования, подставляем полученные функции g_i(y₁,…, y_m).

В результате имеем набор функций

a₁,…, a_k, g₁(y₁,…, y_m),…, g_p(y₁,…, y_m),… (**)

и формулу

B(a₁,…, a_k, y₁,…, y_m, g₁(y₁,…,y_m),…, g_p(y₁,…,y_m),…) (***)

Определение 4.12. Формула логики предикатов называется замкнутой, если она не содержит свободных предметных переменных.

Определение 4.13. Сколемовская форма – это замкнутая предваренная форма, префикс которой содержит только кванторы всеобщности – .

Приведение формулы логики предикатов к сколемовской форме называется сколемизацией.