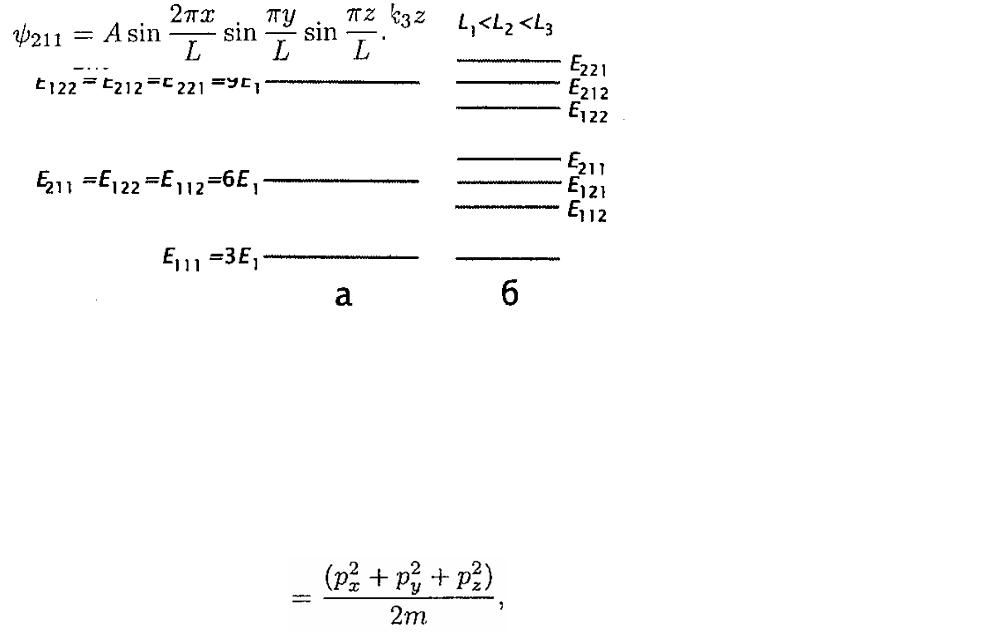
Трехмерное уравнение Шредингерадингера
Схема энергетических уровней случае (а) кубической потенциальной ямы с бесконечно высокими стенками и (б) прямоугольной потенциальной ямы некубической формы с бесконечно высокими стенками.
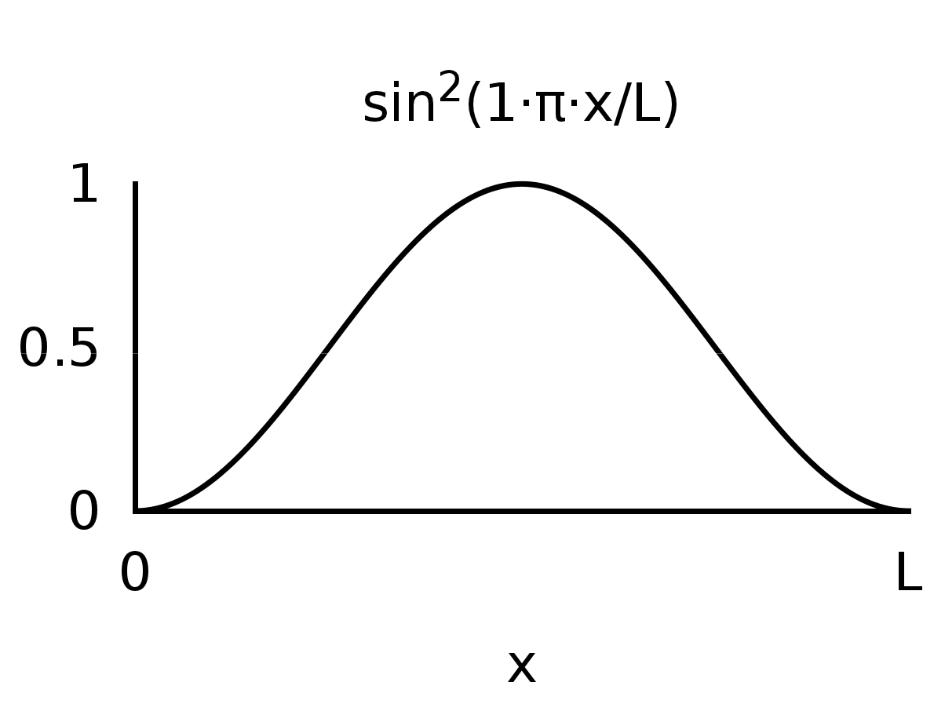
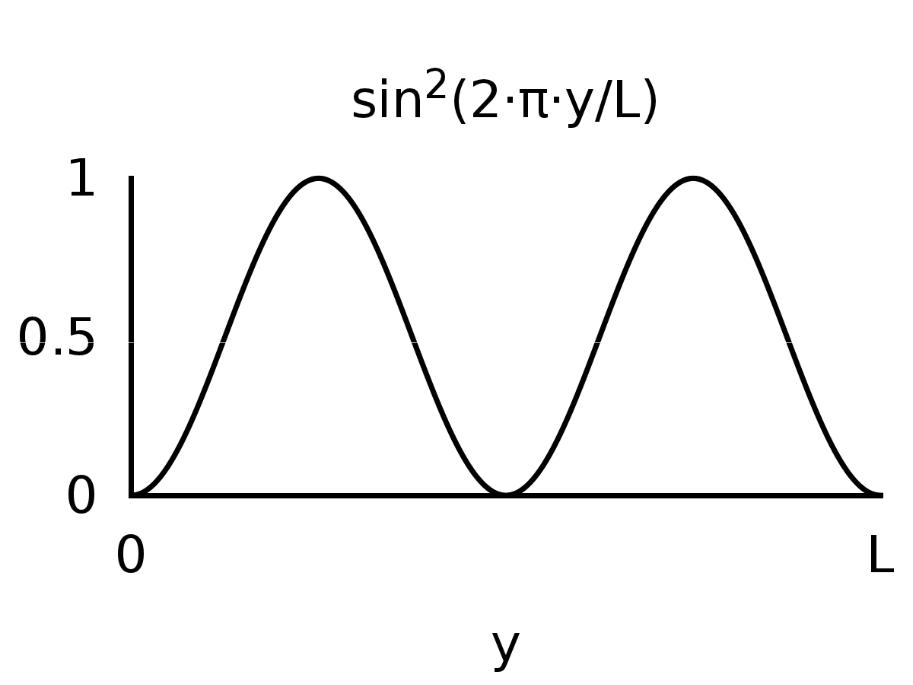
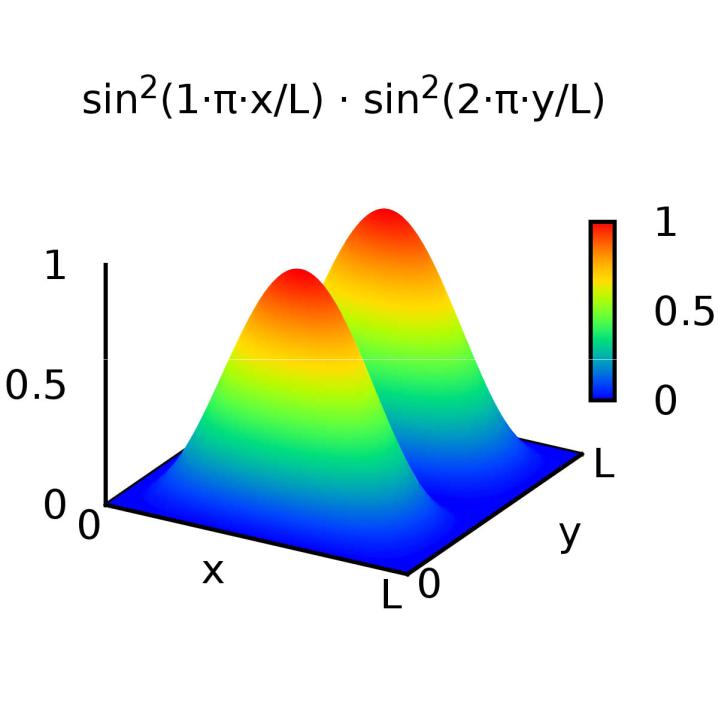
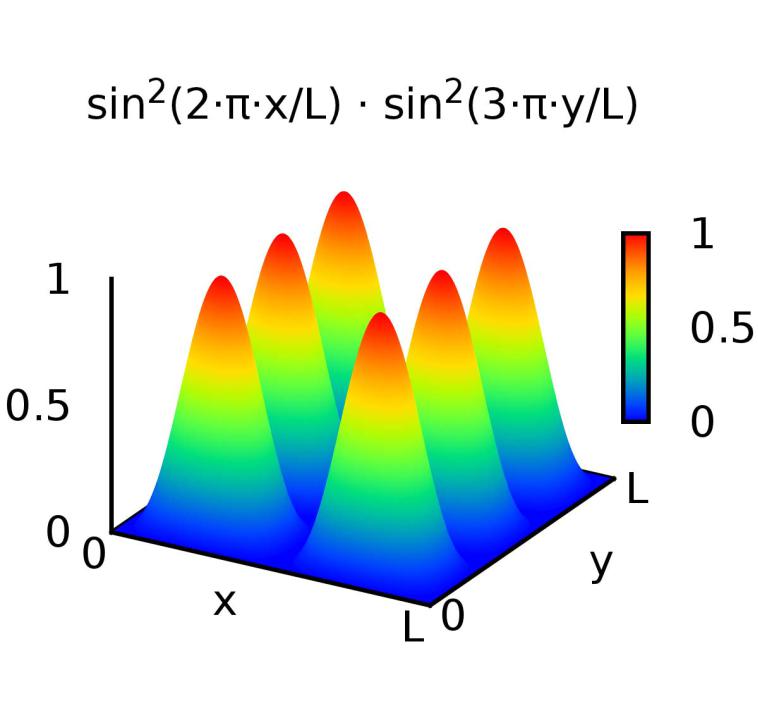
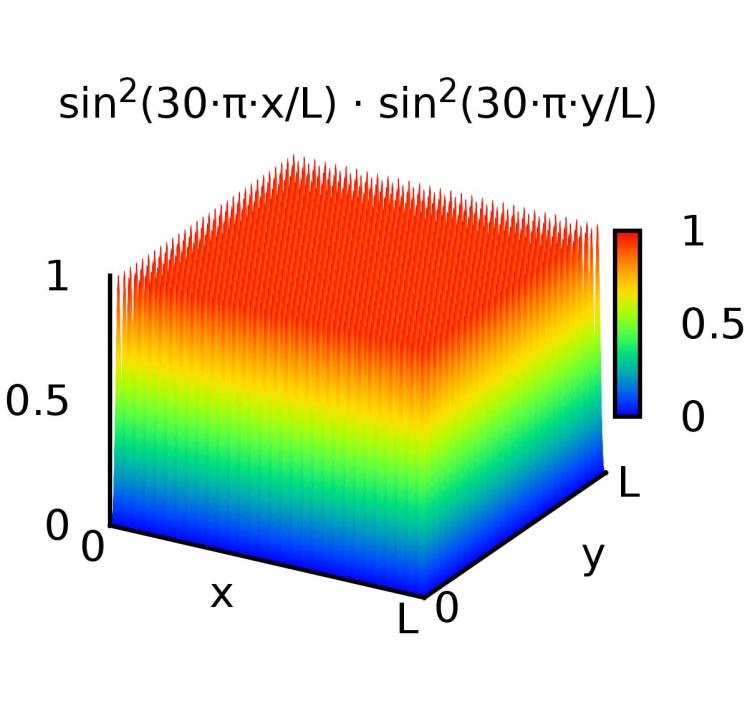
Связанные состоянияя
|
|
|
|
E4 |
E n |
2 2 n 2 |
|
|
E3 |
|
|
|||
|
|
E2 |
||
2 m L2 |
|
|||
|
|
E1 |
||
В отличие от классической частицы, квантовая частица в прямоугольной яме не может иметь энергию
E 2 2 /(2mL2 ) . Состояния бесспиновой частицы n в
одномерном поле бесконечной потенциальной ямы полностью описываются с помощью одного квантового числа n. Спектр энергий в этом случае дискретный.
Пример
Вычислить допустимые уровни энергии электрона, находящегося в прямоугольной потенциальной яме шириной 10 8 см, протона, находящегося в
потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме шириной 1 см.
|
|
|
|
En |
|
2 2n2 |
, |
|
|
n 1, 2, 3,... |
||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2mL2 |
|
|
|
|
|
|||
Электрон ( mc2 0,511 МэВ, |
L 10 8 см): |
|
|
|
|
|
||||||||
|
|
En |
|
(197)2 МэВ2 Фм2 |
(3,14)2 |
n2 |
32,9n2 эВ. |
|||||||
|
|
|
2 0,511 МэВ (10)5 |
Фм2 |
||||||||||
|
|
|
|
|
|
|||||||||
Протон ( mc2 938,3 МэВ, L 5 Фм): |
|
|
|
|
|
|||||||||
|
|
En |
(197)2 МэВ2 Фм2 |
(3,14)2 |
|
n2 |
8,5n2 МэВ. |
|||||||
|
|
|
2 938,3 МэВ (5)5 Фм2 |
|||||||||||
|
|
|
|
|
|
|||||||||
Шарик ( m 1 г, L 1 см): |
|
|
|
|
|
|
|
|
|
|||||
En |
|
(197)2 МэВ2 Фм2 (3,14)2 1,6 10 6 |
|
n2 |
3, 4 10 42 n2 эВ. |
|||||||||
2 (3 1010 см/сек)2 (1013 )2 Фм2 |
||||||||||||||
|
|
|
|
|
|
|
||||||||
Гамильтониан
Общий вид: H E U
Свободная частица:
H 2 2m
Частица в одномерной потенциальной яме U(x):
|
|
2 |
|
d |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
H |
|
|
|
|
|
|
|
U(x), |
|
0 x L |
||||||||||
2m |
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гармонический осциллятор: |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
d2 |
2 |
x |
2 |
|
||||||||
H |
|
|
|
|
|
|
|
|
m |
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Атом водорода: |
H |
2 |
e2 |
|
|
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
2m |
|
|
|
||||||
|
|
|
|
|
|
r |
|
|
|
|||
Атом гелия: |
|
|
|
|
|
|
|
2e2 |
2e2 |
e2 |
|
|
H |
2 |
|
2 |
|
|
|
. |
|||||
|
|
|
|
|
||||||||
|
2m |
1 2m |
2 |
|
r1 |
r2 |
r12 |
|||||
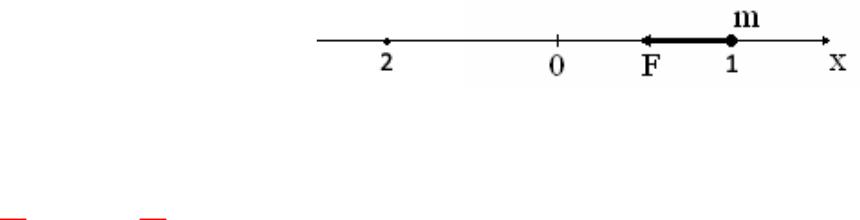
Классический гармонический осцилляторллятор (1)(1)
Частица движется под действием силы F kx
Уравнение движения
m |
d 2 x |
k x |
||
d t |
2 |
|||
|
|
|||
Сумма кинетической и потенциальной энергий осциллятора постоянна
12 mv 2 12 kx 2 E const
Обозначим 2 k / m
Решение уравнения движения определяет положение частицы
взависимости от времени
xA cos t D sin t
начальные условия t 0 |
x L |
v 0 |
Екл 12 mL2 2 sin2 t 12 kL2 cos2 t
Классический гармонический осцилляториллятор (2)(2)
Полная энергия классического гармонического
осциллятора
Екл 12 mL2 2 sin 2 t 12 kL2 cos2 t
Зависимость координаты и скорости частицы от времени
x(t) L cos t
v(t) L sin t
В крайних положениях частица имеет максимальное значение
потенциальной энергии
E 12 m 2 L2
При прохождении положения равновесия частица имеет максимальную
кинетическую энергию
E 12 m 2 L2