Квантовый гармонический осциллятор (1)

Задача сводится к решению уравнения Шредингера

	2		d 2		m 2 x2	E
	2m dx2
				2

Волновая функция не локализована в какой-либо точке оси x . Поэтому

соотношение F kx не может быть применено для решения задачи как в классическом случае.

Нельзя получить в качестве решения соотношения

x(t) L cos t, v(t) L sin t

При квантово-механическом рассмотрении потенциальная энергия

U m 2 x2

2

является основной исходной величиной, характеризующей квантовую систему гармонического осциллятора.

В отличие от бесконечно ямы движение частицы не ограничено непроницаемой стеной. Единственное требование, накладываемое на волновую функцию она должна стремится к 0 на бесконечности.

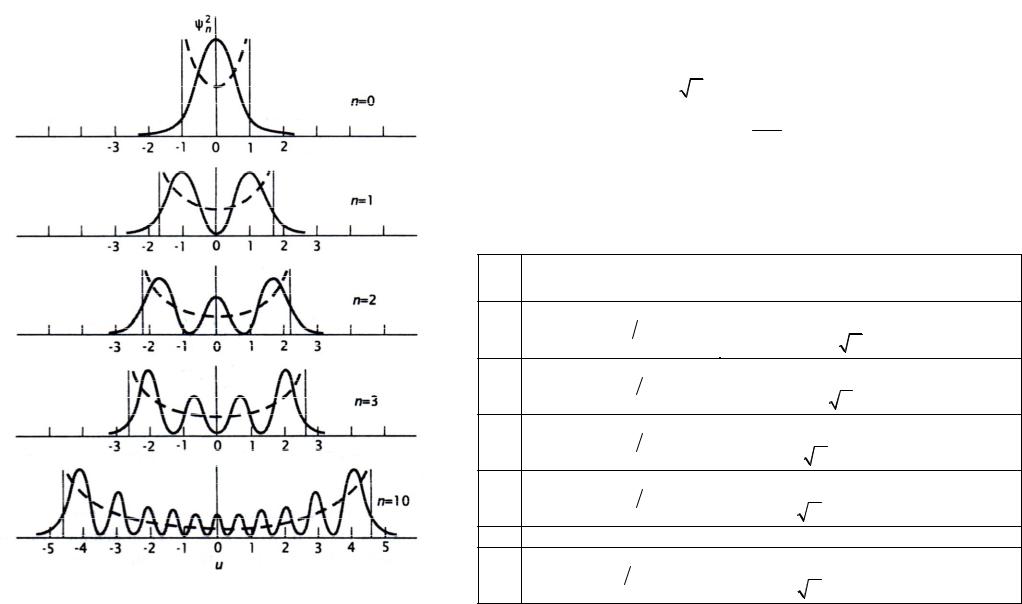
Квантовый гармонический осциллятор (2)

Каждому энергетическому состоянию соответствует волновая функция, описываемая полиномом Эрмита Hn .

		a			1/2		a2 x2 /2
n						Hn (ax)e
		2	n
				n!

Hn ( 1)n e 2 dd nn (e 2 )

где a2 4 2m / , ax . В таблице приведены собственные значения энергии En и нормированные собственные функции гармонического осциллятора n

n

0

1

2

3

▬ ▬ ▬ - классический гармонический осциллятор	n
▬▬▬▬ - квантовый гармонический осциллятор

Собственные

Нормированные собственные

значения энергии En

функции En

E0 2

a

1/2

a2 x2 /2

0

e

E0 3 2

1

a

1/2

2axe

a2 x2

/2

2

E0 5 2

a 1/2

(4a

2

x

2

2)e

a2 x2

/2

2

8

E0 7 2

a

1/ 2

3

3

a2 x2 /2

3

(8a

x

12ax)e

48

En (n 1 2)

a

1/2

a2 x2

/ 2

n

Hn (ax)e

2

n

n!

Пример

Рассчитать расстояние между уровнями 1s, 2s и 3s ядра 90Zr для прямоугольной потенциальной ямы бесконечной глубины и ямы гармонического осциллятора.

Впрямоугольной яме энергии уровней с l 0 определяются

соотношением En (n )2 , 2mR2

n — главное квантовое число, m — масса нуклона и

R— радиус ядра (ширина ямы). Величина расстояний между уровнями 1s, 2s

и3s будет

E				3		( )2			3			( c)2
						2mR2					2mc2 (r A1/3 )2
		1s	2s
											0
			3	(3,14 200)2 МэВ2 Фм2														3 7,3 МэВ 22 МэВ;
		2 931,5									1/3		2	Фм		2
						МэВ (1,2 90 )
	E		2s 3s		5		( )2		5			( c)2					5 7,3 МэВ 36,5 МэВ.
							2mR2					2mc2 (r A1/3 )2
											0

В яме гармонического осциллятора выражение для энергии уровней с l 0

определяется соотношением En	(2n 3/ 2),
41A1/ 3 41 901/ 3 9,1	МэВ	для	90Zr.	Расстояние	будет

E1s 2s E2s 3s 2 18,2 МэВ.

Прямоугольная и сферическая системыы координаткоординат

	Переход от
	прямоугольной системы
	координат к	Элемент объема dτ в
	сферической.
		сферических
		координатах.

Частица в поле с центральной симметриейимметрией

Стационарное уравнение Шредингера частицы в сферически симметричном потенциальном поле U(r)

2

1

r

2

1

(s in

)

1

2

r

2 M

r

r 2 s in

r 2 s in

2 2

r 2

U ( r ) E .

Волновая функция (r, , ) может быть представлена как произведение

радиальной функции Rnl (r)

и угловой функции Ylm ( , )

(r, , ) Rnl (r )Ylm ( , )

Уравнения для нахождения собственных значений и

собственных функций угловой и радиальной функций.

2

1

1

2

( , ) 2l (l

sin

Y

lm

1)Y

lm

( , )

sin

sin 2

2

d

2

2

l ( l

1)

rR nl ( r )

U ( r )

rR nl ( r ) E

rR nl ( r )

2 M

dr

2

2 M r

2

Орбитальный момент количества движенияижения (1)(1)

Собственные значения	операторов		ˆ2	ˆ	являются решением
			L	и Lz
операторных уравнений
ˆ2	2	( , )	ˆ		LzYlm( , )
L Ylm ( , ) L Ylm			LzYlm( , )

Они имеют следующие дискретные значения

L2 2l(l 1), где l 0, 1, 2, 3,...,

Lz m, где m 0, 1, 2, 3, , l .

Сферические функции (их называют также сферическими

гармониками)	Ylm ( , ) являются собственными функциями
ˆ2	ˆ	, т. е. описывают состояния с определенными	l и
операторов L	и Lz

m, а значит и определенными значениями орбитального момента и его проекции на ось z . Сферические функции Ylm ( , ) имеют вид

2l 1

(l

m

)!

Ylm

( , ) ( 1)m

eim

Plm(cos ) ,

4

(l

m

)!

Pl m (cos ) функция Лежандра.

Орбитальный момент количества движенияижения (2)(2)

Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L дается соотношением

L l(l 1) .

Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной число l, имея в виду, что между l и L имеется однозначная связь

L l(l 1) .

Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения квантуется. Например, для частицы с l 2 момент

количества движения

L 2(2 1) 6.58 10 22

6 МэВ с 2.6 10 34 Дж с.

Орбитальный момент L

Проекция орбитального момента Lz

l 0 s состояние

l 1 p состояние

l 2 d состояние

l 3 f состояние

l 4 g состояние

l 5 h состояние

и. т. д.

Оператор квадрата углового момента

2		2		1							1				2
L								(sin		)
											sin	2				2
			sin

Уравнение для нахождения собственных значений и собственных функций оператора

квадрата углового момента L2Ylm ( , ) L2Ylm ( , )

Собственные значения оператора квадрата углового момента

L 2 2 l ( l 1)

l 0, 1, 2, 3, …,

Уравнение для нахождения собственных значений и собственных функций оператора
проекции углового момента	Lz Ylm ( , ) LzYlm ( , )
Собственные значения оператора проекции углового момента

Lz m	m 0, 1, 2... l

Сферические функции

Сферические функции Ylm ( , ) удовлетворяют уравнению

				L2 Y					( , )								2l(l 1) Y															( , ) ,													(*)
						lm							1										lm												1							2
				L2 2															(sin									)																		.
											sin																									2								2
																																	sin
							l 0, 1, 2, …; m l, l 1, …, l.
																		2l 1			(l						m				)!
			Y		( , ) ( 1)m																												eim				Pm (cos )
																		4			(l						m
				lm																												)!						l
Симметрия:								Y				( , ) ( 1)mY																					( , ) .
Ортогональность:										lm													l, m
			sin d						2 Y ( , )Y
																							( , )d
													lm																											ll					mm
			0							0										l m
			Y			1		,		Y								9		cos , Y																		3				sin ei ,
						4												4																				8
			00							10													11
Y		5	3 cos2				1			,	Y									15 sin cos ei																					,		Y						15	sin2 e2i .
																																																	32
20		4 2					2					21								8																									22
Возможные значения орбитального квантового числа																																			l						связаны со свойствами

полинома Лежандра. Решение уравнения (*) существует только в том случае, когда

орбитальное квантовое число l имеет целочисленное значениеение,, включая 0. При

этом оно должно быть больше абсолютного значения m или равно ему.

L=0, mL=0

L=1, mL=±1

L=1, mL=0

L=2, mL=±2

			L=2, mL=±1
	L=2, mL=0

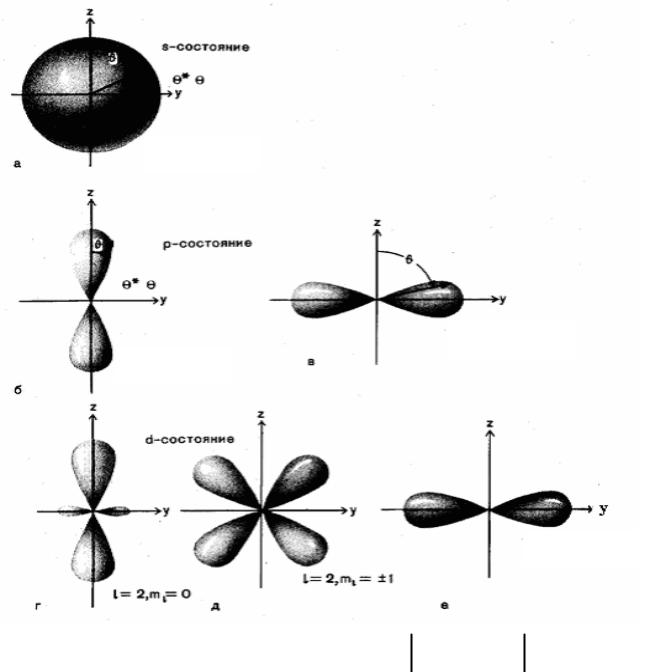
Распределение угловой вероятности Ylm ( , ) 2 d нахождения частицы

в s-, p- и d-состояниях в сферически симметричном потенциале.

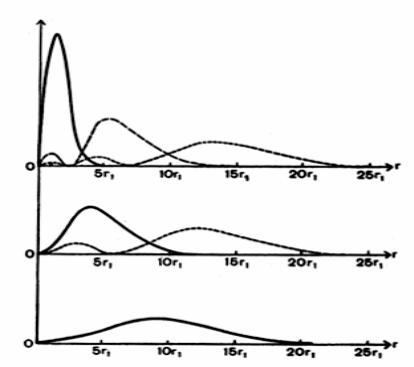
|Rnl(r)|2=r2dr

1s s-состояния

2s 3s

r1 радиус Бора (0.53Å)

2p	p-состояния
	3p

3d d-состояниe

Радиальное распределение вероятности

							2				d		2										2		l(l
																rRnl		(r) U (r)									1)			rRnl (r) E rRnl (r)
				2M dr										2										2Mr			2
																	(r , , ) Rn l (r )Ylm ( , )
	2		1								r	2							1			(sin					)			1 2			U (r) E .
															r
																			r2 sin										r2 sin2 2
	2M r2 r

L=0, mL=0
				L=2, mL=0
		L=1, m =0
		L

Распределение полной вероятности Rnl (r) Ylm ( , ) 2r2drd

нахождения электрона в атоме водорода, определяемое угловой и радиальной плотностью вероятности.

Частица в поле с центральной симметриеймметрией

( r , , ) R n l ( r )Ylm ( , )

Вполе с центральной симметрией сохраняются:

2l(l 1)

m

E– энергия,

-квадрат орбитального момента

-проекция орбитального момента

E, l, m.

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m При этом предполагается, что частица не имеет внутреннего углового момента, то есть спин S частицы равен 0.

n 1, 2, 3...
l 0,1, 2, 3...
m 0, 1, 2...	l

Полный момент количества движенияжения (1)(1)

Полный момент количества движения частицы складывается из
его орбитального момента		L r p	и спинового момента	S :
				(*)
J		L	S
В квантовой теории ситуация аналогичная. Полный момент
количества движения также описывается соотношением,
аналогичным (*), в котором величины J, L и S заменены на
			ˆ	и
операторы полного момента Jˆ, орбитального момента L
спинового момента Sˆ .

В соответствии с общими правилами для квантовых векторов
проекция полного момента на выделенную ось (z) может
принимать 2j 1 значение:			1 / 2 (или 0)
jz j ,	( j 1) ,	( j 2) , ...,

Квантовые вектора (соответствующие им квантовые числа l, s и j) не могут принимать непрерывный ряд значений, а всегда обязаны быть либо целыми (возможен и нуль), либо полуцелыми числами.

Полный момент количества движенияжения (2)(2)

Следствием этого является правило сложения квантовых векторов

l s j l s,

Левая часть этого неравенства соответствует минимальному значению вектора , когда вектора l и s направлены в

противоположные стороны. Правая часть неравенства отвечает максимальному , когда l и s направлены в одну

сторону. С учетом требований пространственного квантования

все возможные j заключены в интервале от l s до l s и

изменяются в пределах этого интервала с шагом 1.

Для проекций jz , lz , sz существует простое алгебраическое

соотношение

jz lz sz

Пример

Сложение спинового s и					орбитального l моментов
									о l моментов
J		l		s
			2							1
	l						s			2
							3		5
								,		.
	J		l	s			2		2

Пример

		Сложение полных моментов
J		J1 J2
J 1 J 2			J	| J1	J 2	|
			через единицу
J1		2		J2 3
	1, 2, 3, 4, 5.
J
J1		3 / 2		J2	2
	7 / 2, 5 / 2, 3 / 2, 1 / 2.
J

Квантовые состояния. Учет спинаспина

( x , y , z )

| nlj

n - номер состояния с данным l l - орбитальный момент

j - полный момент

s - спин

1 d5/2

R n l ( r )Y lm ( , )

j l s

E, Jp

n l

j

Связанные состояния в центральносимметричном поле описываются определённым набором квантовых чисел. n определяет уровни энергии связанных состояний частицы.