Выводы

1. Частица в бесконечной прямоугольной яме

En 2 2n2 , n 1, 2, 3, ...

2mL2

Минимальная энергия любой частицы в потенциальной яме не может быть равна нулю.

	n		2	sin	nx	,	n 1, 2, 3, ...
			L		L

2. Уравнение Шредингера

ˆ i t H

ˆ

H - оператор полной энергии

3. Стационарное уравнение Шредингера

		2			d 2	U		(x) (x) E (x)
		2m dx2
	4. Квантовый гармонический осциллятор						1
	En		n						,	n 0,1, 2, ...
							2

				n
5.	Бесспиновая частица в поле с центральной симметрией
	(r, , ) Rnl (r)Ylm ( , )
	En				n 1, 2, 3,...
	lZ 0, 1, 2, ..., l,				l 1, 2, 3,...
6.	Орбитальный момент количества движения
	ˆ2	2	l(l	1)Ylm ( , ),		l 0, 1, 2, ...
	L Ylm ( , )
7.	Lz	m,			m 0,1, 2, ...
	Полный момент количества движения J L S

JZ J , J 1, ..., (0,1/ 2)

Стационарное уравнение Шредингера (1)

В случае одного пространственного измерения уравнение Шредингера имеет вид

i (x,t)

2

2

V (x,t) (x,t)

(1)

2m x2

t

В случае, если потенциальная энергия V (x,t) не зависит от времени V (x,t) V (x) , пространственная и

временная зависимости могут быть разделены. Представим функцию (x,t) в виде

(x,t) (x) (t) .

(2)

Подставив соотношение (2) в уравнение (1), получим

i

(x) (t)

2

2 (x) (t)

V (x) (x) (t).

(3)

2m

t

x2

Разделив уравнение (3) на (x,t) (x) (t)

и перейдя от частных производных к обычным производным,

получим

i

1 d (t)

2

1

d 2 (x)

V (x)

(4)

(t) dt

2m (x) dx2

Левая и правая части уравнения (4)

зависят только от одной переменной x или t . Т.е. изменение t

в левой

части уравнения не влияет на правую часть уравнения, а изменение x в правой части уравнения не влияет на левую часть уравнения. Следовательно, обе части уравнения должны равняться одной и той же постоянной С.

Таким образом, уравнение (3), являющееся уравнением в частных производных, можно заменить на

два уравнения, каждое из которых зависит только от одной переменной x или t .
			i	1				d		C	(5)
				(t) dt
	2	1				d 2			V (x) C		(6)
	2m (x) dx2

Стационарное уравнение Шредингера (2)

Постоянная С называется постоянной разделения переменных. Для решения уравнения (5) представим его в виде

d (t)		C dt iC dt
(t)		i

Решение уравнения (7) имеет вид

(t) exp iCt

Функцию (t) можно представить в виде

			iCt		Ct
	(t) exp				cos			i sin

(7)

(8)

	Ct			(9)

Таким образом, функция (t) , описывающая изменение (x,t) , представляет собой осциллирующую со временем функцию с частотой

	C .	(10)

Однако в силу соотношения де Бройля частота волны описываемой волновой функцией (x,t) есть

			E	.			(11)
Отсюда следует, что постоянная С разделения переменных
		C E ,					(12)
где E представляет собой полную энергию частицы.					iEt
		(t) exp				.	(13)
Подставив постоянную C E в уравнение (6), получим
	2	d 2 V (x) (x) E (x)					(14)
	2m dx2

Уравнение (14) называет стационарным уравнением Шредингера. Для получения закона движения частицы – волновой функции (x,t) кроме уравнения Шредингера должны быть заданы также начальные и граничные условия.

Квантовый гармонический осциллятор (1)

Уравнение Шредингера для линейного гармонического осциллятора имеет вид

	2		d 2			m 2 x2		E (1)
	2m dx2
							2
Введем безразмерные переменные
				m			x,		2E	(2)

Уравнение (1) примет вид

d 2 2 (3) d 2

Случай Решение, удовлетворяющее условию ( ) 0 при

A me 2 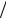2 (4)

m - любое конечное число

Будем искать решение уравнения (3) в виде

f e 2 2 (5)

где f - функция, которая ведет себя на бесконечности как m Подставляя (5) в соотношение (3) получим уравнение для f

	d 2 f	2	df	( 1) f	0 (6)
	d 2		d