Вопрос 1
Если голономная
механическая
система описывается лагранжианом 
(
— обобщённые
координаты, t — время,
точкой обозначено дифференцирование по
времени) и в системе действуют
только потенциальные
силы,
то уравнения Лагранжа второго рода
имеют вид
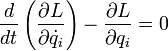
где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы.
Количеством движения системы материальных точек называется векторная сумма количеств движений отдельных точек системы.
Единицей измерения количества движения в СИ является —
Количество движения системы можно выразить через массу системы и скорость центра масс.
Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы.
Теорема об изменении количества движения системы утверждает[2][3]:
Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени.
Пусть система
состоит из 
материальных
точек с
массами 
и
ускорениями 
.
Все силы, действующие на тела системы,
разделим на два вида:
Внешние силы — силы, действующие со стороны тел, не входящих в рассматриваемую систему. Равнодействующую внешних сил, действующих на материальную точку с номером i обозначим
.Внутренние силы — силы, с которыми взаимодействуют друг с другом тела само́й системы. Силу, с которой на точку с номером i действует точка с номером k, будем обозначать
,
а силу воздействия i-й
точки на k-ю
точку — 
.
Очевидно, что при 
,
то 
Используя введённые обозначения, запишем второй закон Ньютона для каждой из рассматриваемых материальных точек в виде
Учитывая, что 
и
суммируя все уравнения второго закона
Ньютона, получаем:
Выражение 
представляет
собой сумму всех внутренних сил,
действующих в системе. По третьему
закону Ньютона в этой сумме каждой
силе 
соответствует
сила 
такая,
что 
и,
значит, выполняется 
Поскольку
вся сумма состоит из таких пар, то и сама
сумма равна нулю. Таким образом, можно
записать
Используя для
количества движения системы 
обозначение 
,
получим
Введя
в рассмотрение изменение импульса
внешних сил 
,
получим выражение теоремы об изменении
количества движения системы в
дифференциальной форме:
Таким образом, каждое из последних полученных уравнений позволяет утверждать: изменение количества движения системы происходит только в результате действия внешних сил, а внутренние силы никакого влияния на эту величину оказать не могут.
Проинтегрировав
обе части полученного равенства по
произвольно взятому промежутку времени
между некоторыми 
и 
,
получим выражение теоремы об изменении
количества движения системы в интегральной
форме:
где 
и 
—
значения количества движения системы
в моменты времени 
и 
соответственно,
а 
—
импульс внешних сил за промежуток
времени 
.
В соответствии со сказанным ранее и
введёнными обозначениями выполняется
