БИЛЕТ 1

Вопрос 1

Количеством движения системы будем называть векторную величину , равную геомет­рической сумме (главному вектору) количеств движения всех точек системы (рис.44):

Из чертежа видно, что независимо от величин скоростей точек системы (если только эти скорости не параллельны) вектор  может принимать любые значения и даже оказаться равным нулю, когда многоугольник, построенный из векторов , замкнется. Следова­тельно, по величине  нель­зя полностью судить о ха­рактере движения системы.                                                                

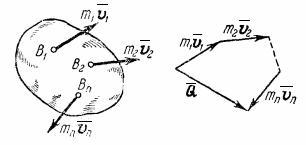
Рис.44

 

Найдем формулу, с по­мощью которой значительно легче вычислять величину , а также уяснить ее смысл.

Из равенства  следует, что 

Беря от обеих частей производную по времени, получим

 или  

Отсюда находим, что 

т.е. количество движения системы равно произведению массы всей системы на скорость ее центра масс. Этим результатом особенно удобно пользоваться при вычислении количеств движения твердых тел.

Из формулы видно, что если тело (или система) движется так, что центр масс остается неподвижным, то количество движения тела равно нулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс, будет равно нулю.

Если же движение тела является сложным, то величина  не будет характеризовать вращательную часть движения вокруг центра масс. Например, для катящегося колеса  независимо от того, как вращается колесо вокруг его центра масс С.

Таким образом, количество движения характеризует только поступательное движение системы. При сложном же движении величина  характеризует только поступательную часть движения системы вместе с центром масс

Теоре́ма об измене́нии коли́чества движе́ния (и́мпульса) систе́мы — одна из общих теорем динамики[1], является следствием законов Ньютона. Связывает количество движения с импульсом внешних сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь идёт речь в теореме, может выступать любая механическая система, состоящая из любых тел[2][3].

Формулировка теоремы[править | править исходный текст]

Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы.

Теорема об изменении количества движения системы утверждает:

Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени.

Пусть система состоит из  материальных точек с массами  и ускорениями . Все силы, действующие на тела системы, разделим на два вида:

• Внешние силы — силы, действующие со стороны тел, не входящих в рассматриваемую систему. Равнодействующую внешних сил, действующих на материальную точку с номером i обозначим .

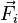• Внутренние силы — силы, с которыми взаимодействуют друг с другом тела само́й системы. Силу, с которой на точку с номером i действует точка с номером k, будем обозначать 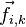, а силу воздействия i-й точки на k-ю точку — 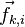. Очевидно, что при , то 

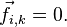
Используя введённые обозначения, запишем второй закон Ньютона для каждой из рассматриваемых материальных точек в виде

Учитывая, что  и суммируя все уравнения второго закона Ньютона, получаем:

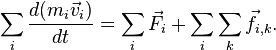
Выражение  представляет собой сумму всех внутренних сил, действующих в системе. По третьему закону Ньютона в этой сумме каждой силе  соответствует сила  такая, что  и, значит, выполняется  Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, можно записать

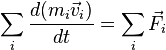
Используя для количества движения системы  обозначение , получим

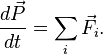
Введя в рассмотрение изменение импульса внешних сил , получим выражение теоремы об изменении количества движения системы в дифференциальной форме:

Таким образом, каждое из последних полученных уравнений позволяет утверждать: изменение количества движения системы происходит только в результате действия внешних сил, а внутренние силы никакого влияния на эту величину оказать не могут.

Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторыми  и , получим выражение теоремы об изменении количества движения системы в интегральной форме:

где  и  — значения количества движения системы в моменты времени  и  соответственно, а  — импульс внешних сил за промежуток времени . В соответствии со сказанным ранее и введёнными обозначениями выполняется

Теоре́ма о движе́нии це́нтра масс (це́нтра ине́рции) системы — одна из общих теорем динамики, является следствием законов Ньютона. Утверждает, что ускорение центра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему

Формулировка теоремы[править | править исходный текст]

Нередко при рассмотрении движения системы полезно знать закон движения её центра масс. В общем случае этот закон, составляющий содержание утверждения теоремы о движении центра масс системы, формулируется следующим образом[1]:

Произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил.

Пусть система состоит из  материальных точек с массами  и радиус-векторами . Как известно^[1][3], центром масс (центром инерции) системы материальных точек называется геометрическая точка, радиус-вектор  которой удовлетворяет равенству

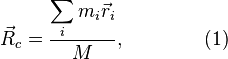
где  — масса всей системы, равная 

Дифференцируя (1) два раза по времени, для ускорения центра масс  получаем:

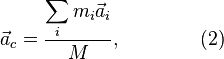
где  — ускорение материальной точки с номером i.

Для последующего рассмотрения целесообразно разделить все силы, действующие на тела системы, на два типа:

• Внешние силы — силы, действующие со стороны тел, не входящих в рассматриваемую систему. Равнодействующую внешних сил, действующих на материальную точку с номером i обозначим .

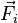• Внутренние силы — силы, с которыми взаимодействуют друг с другом тела само́й системы. Силу, с которой на точку с номером i действует точка с номером k, будем обозначать 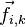. Соответственно, сила воздействия i-й точки на k-ю точку будет обозначаться 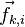. Из сказанного очевидно, что если , то 

Используя введённые обозначения, второй закон Ньютона для каждой из рассматриваемых материальных точек можно записать в виде

Суммируя все уравнения вида (3), получим:

Выражение  представляет собой сумму всех внутренних сил, действующих в системе. Учтём теперь, что по третьему закону Ньютона в этой сумме каждой силе  соответствует сила  такая, что  и, значит, выполняется Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, из (4) следует

Далее, обозначив  и подставив полученное выражение в (2), приходим к уравнению

 или к 

Таким образом, движение центра масс определяется только внешними силами, а внутренние силы никакого влияния на это движение оказать не могут. Формула (6) является математическим выражением теоремы о движении центра масс системы.