§2. Марковские процессы

2.1. Последовательности зависимых испытаний. Цепи Маркова.

Ранее (часть I) мы подробно рассмотрели последовательности независимых испытаний. В этом пункте мы рассмотрим пример одного важного случая последовательности зависимых испытаний.

Будем производить ряд последовательных испытаний, в результате каждого из которых может наступить или не наступить некоторое событие А.

Пусть в случае наступления события А при n-м по порядку испытании

вероятность его наступления при (n +1) -м испытании равна а, а в случае его

не наступления при n-м испытании вероятность его наступления при (n +1) –м испытании равна b. Очевидно, 0 ≤ a, b ≤ 1.

Замечание 2.1. Важность представленного выше результата состоит в том, что это достаточно естественное качественное утверждение получает через формулу доверительного интервала для вероятности p с коэффициентом доверия α вполне определенную количественную интерпретацию:

Поставим следующую задачу: зная вероятность p₁ его наступления при первом по порядку испытании, определить вероятность p_n его наступления при каждом n-м испытании.

Пусть A_n - событие, означающее наступление события А при n-м испытании. Тогда, поскольку событие A_n и противоположное ему событие прикаждом данном значении n образуют полную группу событий. то по формуле полной вероятности получаем:

Согласно введенным выше обозначениям,

Поэтому

^(2.1.1)

Найдем из уравнений (1) величину вероятности p_n как функцию от ве-

личин n (n ≥ 2), a, b и p₁ .

Заметим, прежде всего, что величина

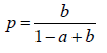
решает уравнение

p = ap + b(1− p) , (2.1.2)

в которое превращается уравнение (1) при p_n ≡ p для всех n.

Для решения уравнения (1) положим p_n = p + p_n* , где p – решение урав-

нения (2). Подставляя это в (1), получим для определения p_n* рекуррентные соотношения

откуда, принимая во внимание (2):

Последнее соотношение, очевидно, дает

Переходя от получим:

или

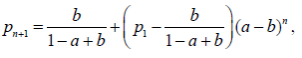(2.1.3)

что и решает нашу задачу.

Примечание. Последняя формула справедлива при a ≠ 1, либо b ≠ 0 . В

том крайнем случае, когда одновременно a =1, b = 0, из (1) получаем сразу

Этот тривиальный частный случай, очевидно, практически малоинтересен.

Если 0 ≤ a < 1 и 0 < b ≤ 1, то соотношение (3) показывает, между про-

чим, что при n → ∞ общее решение имеет вполне определенный предел, не зависящий от p₁ , а именно:

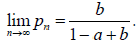
Рассмотренный выше пример последовательности зависимых испыта-ний представляет собой частный случай так называемых цепей Маркова, ко-торые имеют большое прикладное значение.

Пусть дана последовательность дискретных случайных величин ξ₁, ξ₂, …, ξ_n, …, имеющих одинаковые конечные или счётные множества возможных значений. Все случайные величины ξ_k связаны таким образом, что значение, принятое величиной ξ_{k – 1} , вполне определяет закон распределения случайной величины ξ_k , и этот закон не зависит от значений принятых случайными ξ_j с j < k – 1. Используя соответствующие условные вероятности можно записать основное свойство цепей Маркова – марковское свойство:

P{ ξ_k | ξ₁, ξ₂, …, ξ_{k – 1}} = P{ ξ_k | ξ_{k – 1}}

Такая последовательность называется простой цепью Маркова.

Иначе: пусть некоторая физическая система находится в одном из состояний E₁, E₂, …, E_k, … . В фиксированные моменты времени t₁, t₂ , …, t_n , … система под влиянием случайных факторов может переходить из одного состояния в другое, причём в любой момент времени t_k вероятность системе оказаться в наперёд заданном состоянии E_j вполне определяется тем состоянием, в котором она находилась непосредственно перед скачком, и не зависит от всех остальных состояний, в которых эта система находилась до момента t_{k – 1} ; тогда говорят, что поведение этой системы описывается (или управляется) простой цепью Маркова;

– вероятность перехода из состояния E_i (в момент t_{n – 1}) в состояние E_j в момент t_n называется переходной вероятностью этой цепи.

Замечание 2.2. Можно также ввести понятие сложной цепи Маркова порядка m (m > 1), если вероятность случайной величины ξ_k (как правило, это значение случайного процесса в момент времени t_k) зависит только от m случайных величин непосредственно предшествовавших ξ_k :

P{ ξ_k | ξ₁, ξ₂, …, ξ_{k – 1}} = P{ ξ_k | ξ _{k – m} , ξ _{k –m + 1}, …, ξ_{k – 1}.

Так как известна методика, при помощи которой сложная цепь Маркова порядка m может быть сведена к простой цепи Маркова для m-мерного вектора, то можно ограничиться рассмотрением только простых цепей.

Цепь Маркова задаётся матрицами перехода (переходными матрицами; матрицами переходных вероятностей) π⁽ⁿ⁾ = , элементами которой являются вероятности перехода в момент t_n, и вероятностями всех состояний системы в начальный момент времени t₀ = 0. Эти вероятности p₀₁, p₀₂, …, p_0k , … называются начальными вероятностями состояний системы.

Замечание 2.3. Правильнее было бы матрицу перехода и сами переходные вероятности запараметризовать двумя параметрами: π(n, m) = || P{ E_j, t_n | E_i, t_m} ||, определяющими не моменты времени до и после перехода, хотя при мгновенном скачке это не требуется.

Если все переходные вероятности зависят только от разности временных параметров, т. е. π(n, m) = π(n – m), n > m ≥ 0, то цепь Маркова называется однородной.

Если все переходные вероятности не зависят от времени (т. е.= p_ij , n = 1, 2, …), то цепь Маркова называется стационарной. Тогда матрица π будет иметь вид, задаваемый соотношением

, (2.1.4)

причём условие суммирования выполняется при любом фиксированном j, 0 ≤ p_ij ≤ 1. Такая матрица называется стохастической. Если, к тому же, и сумма элементов каждого столбца матрицы равна единице, то такую переходную матрицу называют дважды стохастической.

Обозначим через p_ij(m) – вероятность перехода системы, управляемой однородной цепью Маркова, из состояния E_i в состояние E_j за m «шагов». Матрица перехода через m шагов имеет вид

π_m = .

Тогда (легко доказать по индукции)

π_m = π^m. (2.1.5)

Вероятность p_ij(m) удовлетворяет уравнению Маркова

p_ij(m) = , (2.1.6)

где s может принимать любое целое значение из отрезка [0, m].

Замечание 2.4. Уравнение (2.1.6), а чаще его очевидные обобщения и аналоги, называют также уравнением Смолуховского или уравнением Колмогорова - Чепмена.

Безусловная вероятность p_j (n) = называется абсолютной вероятностью системе оказаться в момент t_n в состоянии E_j.

Эргодическая теорема Маркова. Если существует такое натуральное число n, что все элементы матрицы π_n = πⁿ строго положительные, то для каждого j=1, 2, …, k,… существует предел , не зависящий отi. Вероятности p_j называются финальными вероятностями состояний системы,

; . (2.1.7)

Финальные вероятности p_j являются решением системы линейных уравнений

p_j = , j = 1, 2, …; p_j > 0, (2.1.8)

Цепь Маркова, для которой существуют финальные вероятности, называется эргодической или регулярной. Если все финальные вероятности строго положительны, цепь называется положительно регулярной.

Пусть E = 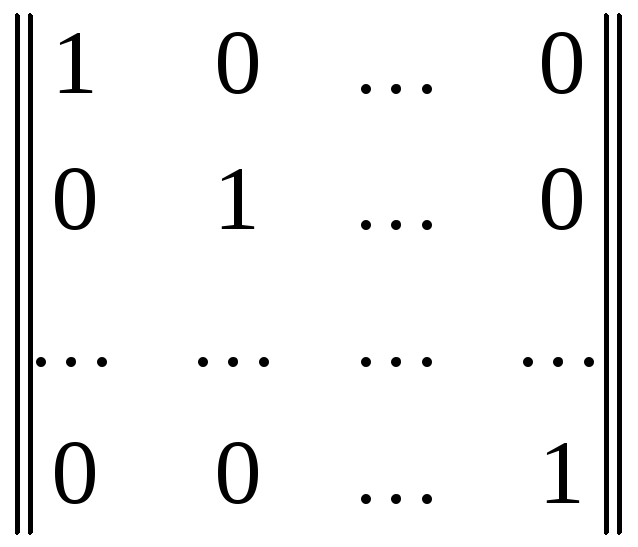– единичная матрица порядка, равного порядку переходной матрицы π (подразумеваются цепи с конечным числом состояний), а λ – параметр. Тогда матрица

|| λ E – π||= 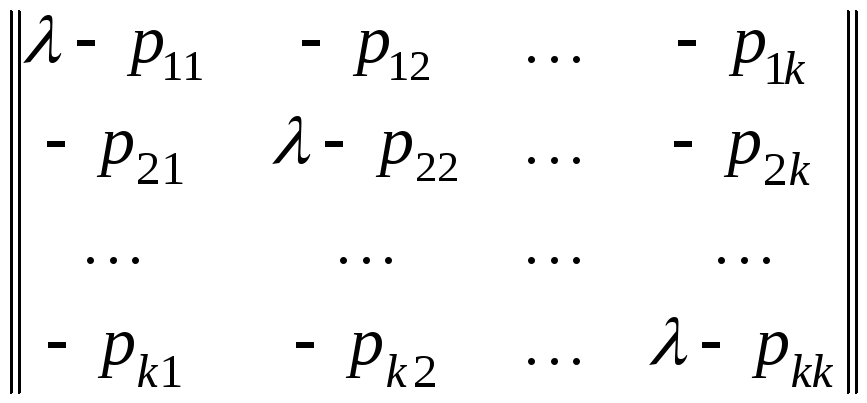(2.1.9)

называется характеристической матрицей данной цепи Маркова. Её определитель обозначается через | λ E – π|, а уравнение

| λ E – π| = 0 (2.1.10)

Называется характеристическим уравнением. Все корни характеристического уравнения называются характеристическими числами матрицы. Одно из них всегда равно 1, а все остальные по модулю не превосходят 1.

Если цепь Маркова эргодична, то все остальные характеристические числа по модулю строго меньше единицы и главные миноры P_{j j} (λ) характеристической матрицы при λ = 1 строго положительны.

Примечание: главным минором P_{j j} (λ) называется минор элемента (λ – p_{j j}) характеристической матрицы.

Тогда финальные вероятности p_j вычисляются по формулам

p_j = 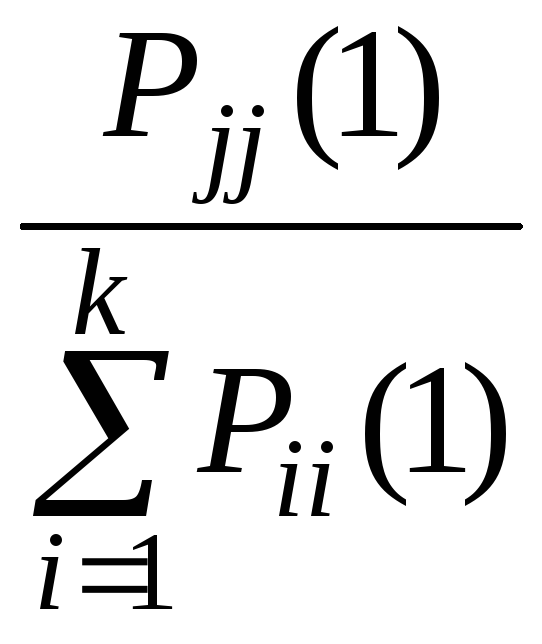. (1.2.11)

Состояние E_i называется несущественным, если существует состояние E_j и целое число k, такие, что из состояния E_j возможен переход в состояние E_i через k шагов, но невозможен возврат из E_i в E_j ни через какое число шагов: p_{i j} (k) > 0, p_{j i} (m) = 0, m = 1, 2, … . Если E_j – несущественное состояние, то p_j = = 0 для любогоi.

Все остальные состояния называются существенными. Если существуют такие целые числа k и m, что p_{i j} (k) > 0, p_{j i} (m) > 0, то состояния E_i и E_j называются связанными или сообщающимися.

Все существенные состояния системы разбиваются на несвязанные (или изолированные) классы состояний. Все состояния каждого из классов связаны. Попав в данный класс, система в дальнейшем не может выйти из него. Если система находится в несущественном состоянии, то с вероятностью 1 она рано или поздно попадёт в один из классов существенных состояний.

Если все состояния системы разбиваются на классы S⁽¹⁾, S⁽²⁾, …, S^(r) , то переходная матрица цепи Маркова перестановкой соответствующих строк и одновременно столбцов с теми же номерами приводится к виду

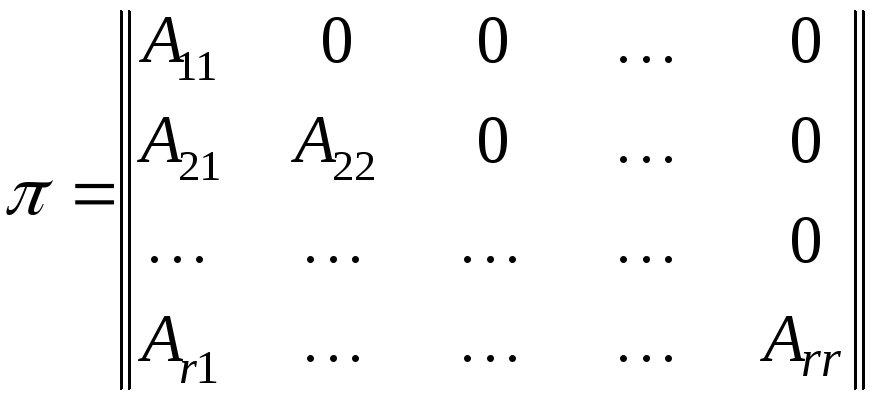, (2.1.12)

где A₁₁, A₂₂, …, A_{r r} – квадратные матрицы порядков числам состояний соответствующего класса S^(j), и более не разложимые подобным образом; нули обозначают подматрицы, все элементы которых равны нулю, а A_{i j} при i ≠ j – какие-нибудь подматрицы (что получится). Такая матрица называется разложимой. Матрица, которую нельзя привести к подобному виду называется неразложимой. Если все A_{i j} = 0 при i < j, то матрица называется вполне разложимой.

Состояние E_j называется возвратным, если система из этого состояния с вероятностью 1 с течением времени снова вернётся в это состояние. В противном случае (т. е. когда вероятность возвращения в это состояние меньше 1) состояние называется невозвратным.

Возвратное состояние с бесконечным математическим ожиданием времени возвращения называется нулевым.

Состояние E_j называется периодическим с периодом m, если возвращение в это состояние возможно лишь за число шагов, кратное m > 1, и m есть наименьшее из целых чисел с этим свойством.

Возвратное состояние, не являющееся ни нулевым, ни периодическим, называется эргодическим.