Теория вероятностей

На рис. 4.1 приведены четыре диаграммы рассеяния, построенные по парным выборкам. На рис. 4.1 (а) приведен пример, когда между величинами Х и Y

существует функциональная линейная связь,

В

. В случае рис. 4.1 (б) следует

между Х и Y,

. На рис. 4.1

предполагать отсутствие какой-либо корреляции= −1

В

В

(в) видно, что Х и Y линейно коррелированы,

4.1 (г) приведен

. На рис. = 0

виде

пример, когда между величинами Х

и

Y

существует корреляция в

= 0,75

параболической кривой, но так как

В = 0

,

то

предположение

о

линейной

корреляции было бы неверным.

Проверим значимость выборочного коэффициента корреляции. Пусть из

двумерной генеральной совокупности (X, Y),

распределенной

нормально,

извлечена выборка объема , по которой

вычислен выборочный коэффициент

корреляции ген

. Требуется проверить нулевую гипотезу Н0:

ген

= 0

,

т.е. о

равенстве нулю

коэффициента корреляции генеральной совокупности.

0

Для проверки гипотезы о значимости выборочного коэффициента корреляции

по выборке (X, Y) составляется специальная характеристика

набл =

∙√

.

(4.6)

и сравнивается с табличным критическим значением

, которое находится

по таблице критических точек распределения Стьюдентакрит( , )(приложение 4) по

заданному уровню значимости и числу степеней свободы

=

—2

, где –

объем выборки.

Критерий.

Если | набл| < крит - нет оснований отвергнуть нулевую гипотезу,

следовательно, случайные величины X и Y некоррелированы.

Если | набл| > крит - нулевую гипотезу отвергают, следовательно,

выборочный коэффициент корреляции значимо отличается от нуля, т.е. X и Y

коррелированны.

4.4.Уравнение прямой регрессии

Уравнение линейной регрессии представляет собой уравнение прямой,

аппроксимирующей (приблизительно описывающей) зависимость между

60

случайными величинами

и . Если

коэффициент

корреляции оказывается

значимым, то находят выборочное уравнение прямой линии регрессии Y на X

по формуле

(4.7)

Если считать, что величина Y=свободнаяВ + В ∙ , а X−зависимаяВ .

от Y, то выборочное

уравнение прямой линии регрессии X на Y находят по формуле

=

В + В ∙

−

В .

(4.8)

В уравнении (4.7) коэффициент

В

называется коэффициентом регрессии Y

на X, в уравнении (4.8) коэффициент

В

называется коэффициентом регрессии X

на Y. Прямые (4.7) и (4.8) пересекаются в точке

. Чем меньше угол между

прямыми, тем сильнее линейная связь между,

X и Y. При линейно

коррелированных величинах

и

при помощи прямой регрессии (4.7) можно

сделать наилучшее предсказание для

при заданном значении или при помощи

прямой регрессии (4.8) предсказать

при заданном значении .

Для сравнения теоретических расчетов и данных наблюдений можно построить эмпирические и теоретические линии регрессии, корреляционное поле

(диаграмму рассеяния).

Пример 4.1. Имеются 100 наблюдений двумерной случайной величины (Х, У).

а) Составить корреляционную таблицу.

б) Вычислить для каждой выборки числовые характеристики: выборочные средние

В и В, выборочные дисперсии	и	, выборочные средние квадратические
отклонения и .

в) Вычислить выборочный коэффициент корреляции и проверить его значимость

(уровень значимости 0,05).

г) Найти выборочные уравнения прямых линий регрессии Y на X и X на Y,

изобразить их на корреляционном поле.

д) Построить эмпирические и теоретические линии регрессии.

61

X	Y	X	Y	X	Y	X	Y	X	Y
168	64	169	57	176	71	166	62	177	72
167	71	165	55	172	73	178	80	167	63
171	62	165	72	181	71	165	68	164	66
172	64	171	67	167	61	162	55	167	61
169	64	173	71	168	63	164	60	180	69
168	68	171	65	169	66	165	68	170	61
163	66	158	57	173	77	176	70	169	61
166	63	162	58	168	71	165	61	175	80
168	50	170	62	163	63	159	60	169	57
162	58	170	65	175	67	178	73	165	55
173	67	157	56	174	74	168	62	156	54
182	76	162	52	174	75	165	69	166	61
179	71	170	73	171	66	163	63	168	65
165	69	173	71	172	66	166	57	173	75
164	59	169	61	163	59	167	67	172	68
175	80	163	67	171	60	173	60	175	80
169	64	169	62	169	75	175	75	164	60
160	61	166	57	161	52	165	63	167	64
167	58	178	73	170	61	167	76	167	62
171	76	165	66	163	58	164	57	165	69

Решение.

а) Составим корреляционную таблицу. Исходя из того что количество испытаний n >20, то данные группируем. Находим Хmin=156, Хmax=181, Ymin=50,

Ymax=80. Пусть число частичных интервалов

. Тогда по формуле (3.3) шаг по

каждую пару,

=

= 3,125

=

= 3,75

оси x равен

, по

оси

y

-= 8

. Просматривая

определяем, в какой сектор она попала. Например, пару (168, 64)

отметим чертой в сектор [165,38-168,5]

[61,25-65]

и т.д. Если пара попала на

границу интервала, то ставим вместо

черты в секторе, точку на границе. Например,

×

две пары (170, 65) и (171,65) попали на границу интервала [168,5-171,63] при Y=65,

поэтому при составлении корреляционной таблицы мы их разделим на соседние секторы поровну. А пару (168, 65), попавшую на границу интервала [165,38168,50], в таблице (4.5) отметим точкой, а в следующей таблице запишем ее в сектор, ближе к центру рассеяния (верхний).

62

Таблица 4.5. Предварительная корреляционная таблица

X	[156-	[159,13-		[162,25		[165,38	[168,5-	[171,63	[174,75	[177,88
Y	159,13]	162,25]		165,38]		-168,5]	171,63]	174,75]	177,88]	-181]
[50-		| | |				|
53,75]
[53,75-	| | |	|		| | |		| |	| |
57,5]
[57,5-	|	| |		| | | | | |		| | | |	| | | | |	|
61,25]
[61,25-				| | |		| | | | | | | |	| | | | |	|
65]
[65-				| | | | | |		| |	| | |	| | |
68,75]
[68,75-				| | | |		| |		| |	| | | |	| | |
72,5]
[72,5-						|	| | |	| | | |	|	| | |
76,25]
[76,25-								|	| | |	|
80]
	Вычислим середины частичных интервалов по							и по
		=		+		=157,56,	= + =160,69 и т.д.

63

Подсчитав все частоты, и распределив граничные точки должным образом,

получаем следующую таблицу

Таблица 4.6. Корреляционная таблица

	157,56	160,69	163,81	166,94	170,06	173,19	176,31	179,44
51,88		3		1					4
55,63	3	1	3	2	2				11
59,38	1	2	6	4	5	1			19
63,13			3	9	6	1			19
66,88			6	2	4	3			15
70,63			4	2		2	4	3	15
74,38				1	3	4	1	3	12
78,13						1	3	1	5
	4	6	22	21	20	12	8	7	100

б) Составим статистические законы распределения частот выборки Х и Y

отдельно.

Таблица 4.7.

xi	157,56			160,69		163,81		166,94	170,06		173,19		176,31		179,44	Итого
	4			6		22		21	20		12		8		7	100
															Таблица 4.8.
		51,88		55,63		59,38		63,13		66,88		70,63		74,38	78,13	Итого
		4		11		19		19		15		15		12	5	100

Используя формулы (3.7-3.10), вычислим числовые характеристики для Х и Y.

Выборочные средние

В = (157,56∙4+160,69∙6+163,81∙22+166,94∙21+170,06∙20+

+173,19∙12+176,31∙8+179,44∙7)/100 = 168,5;

64

В= (51,88∙4+55,63∙11+59,38∙19+63,13∙19+66,88∙15+

+ 70,63∙15+74,38∙12++78,13∙5)/100 = 64,93;

Выборочные дисперсии

= (157,56 ∙4+160,69 ∙6+163,81 ∙22+166,94 ∙21+170,06 ∙20+ +173,19 ∙12+176,31 ∙8+179,44 ∙7)/100 −168,5 = 30,1758.

и= 47,6663;

Выборочные средние квадратические отклонения

Найдем

=

30,1758 = 5,49;

и

=

47,6663

= 6,90.

√

=

,

.

;

условные средние , при фиксированных значениях

=

,

∙

,

∙

= 56,56

=

,

∙

,

∙

,

∙

= 55

=

,

∙

,

∙

,

∙

,

∙

,

∙

= 63,47;

=

,

∙

,

∙

,

∙

,

∙

,

∙

,

∙

,

∙

= 62,77

,

,

∙

,

∙

,

∙

,

∙

,

∙

;

Вычисления занесем в таблицу= 70,00;

= 73,91;

= 73,30.

Аналогичным=

образом находим

= 63,88

Таблица 4.9.

157,56

160,69

163,81

166,94

170,06

173,19

176,31

179,44

56,56

55

63,47

62,77

63,88

70

73,91

73,30

Если точки с координатами (

) из таблицы 4.9 отметить на плоскости и

соединить ломаной линией, то получим,

эмпирическую кривую регрессии

на .

Аналогично

найдем

условные

средние

,

при

фиксированных

значениях

= .

=

, ∙

,

∙

= 162,25,

=

,

∙

,

∙

,

∙

,

∙

, ∙

= 163,53;

= 165,95;

= 167,76,

= 167,77;

= 171,94;

= 176,31;

= 176,31.

Вычисления занесем в таблицу

Таблица 4.10.

65

				51,88			55,63				59,38	63,13	66,88		70,63	74,38	78,13
				162,25			163,53				165,95	167,76	167,77		171,94	173,71	176,31
		Точки (				) из таблицы 4.10, отмеченные на									плоскости и соединенные
ломаной линией,, изображают эмпирическую кривую регрессии																на .
		в) Вычислим выборочный коэффициент корреляции. Для этого найдем
среднее произведения										по формуле (4.5).

= (51,88(3∙160,69+1∙166,94)+55,63(3∙157,56+1∙160,69+3∙163,81

+2∙166,94+2∙170,06)+59,38(1∙157,56+2∙160,69+6∙163,81+4∙166,94+

+5∙170,06+1∙173,193)+63,13(3∙163,81+9∙166,94+6∙170,06+ 1∙ 173,19)+

+66,88(6∙163,81+2∙166,94+4∙170,06+3∙173,19)+

+70,63(4∙163,81+2∙166,94+2∙173,19+4∙176,31+3∙179,44)+

+74,38(1∙166,94+74,38∙3∙170,06+4∙173,19+1∙176,31+3∙179,44)+

+78,13(1∙173,19+3∙176,31+1∙179,44))/100 = 10964,94

Тогда по формуле (4.4) выборочный коэффициент корреляции равен

Так как В>0, то с ростом Х=	,	, ∙ ,	, ∙ ,	= 0,66	.
растет и У.

Проверим гипотезу Н0: rг=0, т.е. выясним, значим ли выборочный коэффициент корреляции. По таблицам приложения 4 по уровню значимости

= 0,05	и=1,98. По формуле (4.6) находим						= 100 −2 = 98	находим
	числу	степеней	свободы
крит(0,05,98)		набл =	, ∙√			= 8,72	.
			,

Поскольку | набл| > крит, то нулевую гипотезу отвергаем, и считаем, что выборочный коэффициент корреляции значимо отличается от нуля, т.е. X и Y

коррелированны.

г) Найдем выборочные уравнения прямых линий регрессии Y на X и X на Y.

Подставив наши результаты в (4.7), получаем выборочное уравнение регрессии Y

на X

= 64,93+0,66∙	6,90	(	−168,5)
66	5,49

или после преобразования

= 0,83 − 74,93.

Используя формулу (4.8), находим выборочное уравнение регрессии X на Y

= 168,5+0,66∙	5,49	( −64,93)
	6,90

или после преобразования

= 0,53 +134,09.

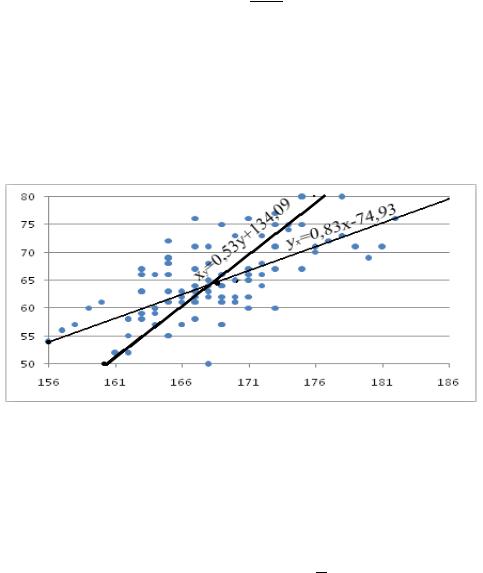
Изобразим на одном рисунке (рис.4.1) графики полученных прямых линий регрессии Y на X и X на Y, а точками – статистические данные (корреляционное поле).

Рис. 4.2. Корреляционное поле и графики теоретических линий регрессии Y на X и X на Y.

д) Построим эмпирическую и теоретическую линии регрессии Y на X на одном чертеже (рис. 4.3). Эмпирическую кривую регрессии Y на X построим,

соединяя ломаной восемь точек с координатами (	), взятыми из таблицы 4.9.
Теоретическую линию регрессии Y на X построим по,	двум точкам с координатами
(156; 54,55) и (186; 79,45).

67

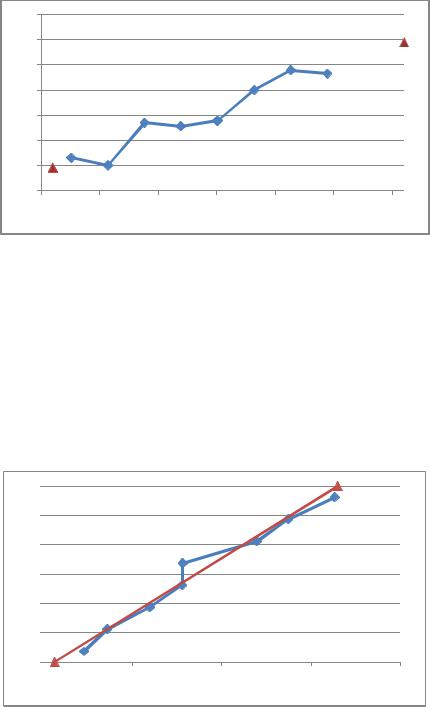
Рис. 4.3. Эмпирическая (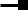 ) и теоретическая ( ) линии регрессии Y на X.

Аналогично, используя таблицу 4.10, построим эмпирическую линию регрессии и, соединяя прямой две точки с координатами (160,59; 50) и (176,49; 80),

теоретическую линию регрессии X на Y (рис. 4.4).

Рис. 4.4. Эмпирическая ( ) и теоретическая ( ) линии регрессии X на Y.

На рис. 4.3. и 4.4 видно, что прямые регрессии наилучшим образом выравнивают эмпирические линии регрессии. На рис.4.2 хорошо показано, что концентрация точек около прямых регрессии довольно тесная. Это говорит о том,

что, по-видимому, в генеральной совокупности степень зависимости величин X и Y

высока. Выборочный коэффициент	корреляции	= 0,66	подтверждает, что
	68

случайные величины X и Y тесно связаны друг с другом, корреляционная зависимость Y от X присутствует. Если > 0, то можно заключить, что с ростом

X увеличивается значение величины Y.

69