
- •Дифференциальные уравнения 2-го порядка
- •§1. Методы понижения порядка уравнения.
- •§2. Линейное дифференциальное уравнение 2-го порядка.
- •§3. Определитель Вронского.
- •§4. Структура общего решения лоду 2-го порядка.
- •§5. Лоду 2-го порядка с постоянными коэффициентами.
- •§6. Структура общего решения линейного неоднородного дифференциального уравнения (лнду) 2-го порядка.
- •§7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
- •§8. Метод вариации произвольных постоянных (метод Лагранжа).
- •Линейные уравнения высших порядков
- •§1. Однородное уравнение.
- •§2. Линейное однородное дифференциальное уравнение с постоянными коэффициентами.
§7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
Пусть в уравнении (6.1) коэффициенты постоянны, т.е. уравнение имеет вид:
![]() f(x)
(7.1)
f(x)
(7.1)
где
![]() .
.
Рассмотрим
метод отыскания частного решения ![]() уравнения (7.1) в случае, когда правая
часть f(x)
имеет специальный вид. Это метод
называется методом неопределенных
коэффициентов и состоит в подборе
частного решения в зависимости от вида
правой части f(x).
Рассмотрим правые части следующего
вида:
уравнения (7.1) в случае, когда правая
часть f(x)
имеет специальный вид. Это метод
называется методом неопределенных
коэффициентов и состоит в подборе
частного решения в зависимости от вида
правой части f(x).
Рассмотрим правые части следующего
вида:
f(x)
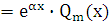 ,
где
,
где  – многочлен степени
– многочлен степени  ,
причем некоторые коэффициенты, кроме
,
причем некоторые коэффициенты, кроме
 ,
могут равняться нулю. Укажем вид, в
котором надо брать частное решение в
этом случае.
,
могут равняться нулю. Укажем вид, в
котором надо брать частное решение в
этом случае.
Если число
 не является корнем характеристического
уравнения для уравнения (5.1), то частное
решение записываем в виде:
не является корнем характеристического
уравнения для уравнения (5.1), то частное
решение записываем в виде:  ,
где
,
где  – неопределенные коэффициенты, которые
подлежат определению методом
неопределенных коэффициентов.
– неопределенные коэффициенты, которые
подлежат определению методом
неопределенных коэффициентов.
Пример
1.
Найти общее решение уравнения ![]() .
.
Решение.
Для
уравнения ![]() составляем характеристическое уравнение:
составляем характеристическое уравнение:
![]() .
Откуда получаем
.
Откуда получаем ![]() ,
,
![]() .
Следовательно, общее решение однородного
уравнения есть
.
Следовательно, общее решение однородного
уравнения есть ![]() .
Правая часть заданного уравнения f(x)
.
Правая часть заданного уравнения f(x)
![]() имеет специальный вид (случай 1), причем
имеет специальный вид (случай 1), причем
![]() не является корнем характеристического
уравнения, поэтому частное решение ищем
в виде:
не является корнем характеристического
уравнения, поэтому частное решение ищем
в виде: ![]() ,
где
,
где ![]() – неопределенные коэффициенты. Найдем
производные первого и второго порядков
и подставим их в заданное уравнение:
– неопределенные коэффициенты. Найдем
производные первого и второго порядков
и подставим их в заданное уравнение:
![]() .
.
Обе
части сокращаем на ![]() и приравниваем коэффициенты при
одинаковых степенях
и приравниваем коэффициенты при
одинаковых степенях ![]() в левой и правой частях равенства
в левой и правой частях равенства
![]()
![]()
Из
полученной системы уравнений находим:
![]() .
Тогда
.
Тогда ![]() ,
а общее решение заданного уравнения
есть:
,
а общее решение заданного уравнения
есть:
![]() .
.
Если
 является корнем кратности
является корнем кратности  соответствующего характеристического
уравнения, то частное решение ищем в
виде:
соответствующего характеристического
уравнения, то частное решение ищем в
виде:
![]() ,
,
где
![]() – неопределенные коэффициенты.
– неопределенные коэффициенты.
Пример
2.
Решить уравнение ![]() .
.
Решение.
Соответствующее характеристическое уравнение имеет вид:
![]() ,
откуда
,
откуда ![]() ,
,
![]() .
Тогда общее решение однородного уравнения
.
Тогда общее решение однородного уравнения
![]() есть:
есть: ![]() .
.
Правая
часть заданного уравнения имеет
специальный вид (случай 1). Так как ![]() является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности ![]() ,
то частное решение ищется в виде:
,
то частное решение ищется в виде:
![]() .
Находим неопределенные коэффициенты
.
Находим неопределенные коэффициенты
![]() методом, изложенным в примере 1. В
результате получаем
методом, изложенным в примере 1. В
результате получаем ![]() .
Окончательно имеем следующее выражение
для общего решения:
.
Окончательно имеем следующее выражение
для общего решения:
![]() .
.
Правая часть f(x)
 ,
где хотя бы одно из чисел
,
где хотя бы одно из чисел  и
и  отлично от нуля. Укажем вид частного
решения в этом случае.
отлично от нуля. Укажем вид частного
решения в этом случае.
Если число
 не является корнем характеристического
уравнения для уравнения (5.1), то частное
решение ищем в виде:
не является корнем характеристического
уравнения для уравнения (5.1), то частное
решение ищем в виде:
![]() ,
,
где
![]() – неопределенные коэффициенты.
– неопределенные коэффициенты.
Если число
 является корнем характеристического
уравнения для уравнения (5.1), причем его
кратность
является корнем характеристического
уравнения для уравнения (5.1), причем его
кратность  ,
то записываем частное решение в виде:
,
то записываем частное решение в виде:
![]() ,
,
где
![]() – неопределенные коэффициенты.
– неопределенные коэффициенты.
Пример
3.
Решить уравнение ![]() .
.
Решение.
Корни
характеристического уравнения для
уравнения ![]() будут
будут ![]() ,
,
![]() .
Тогда общее решение этого лоду:
.
Тогда общее решение этого лоду: ![]() .
.
Правая
часть заданного в примере 3 уравнения
имеет специальный вид: f(x)
![]() ,
где
,
где ![]() ,
а
,
а ![]() .
Число
.
Число ![]() является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности ![]() ,
поэтому частное решение лнду имеет вид:
,
поэтому частное решение лнду имеет вид:
![]() .
.
Для
определения ![]() и
и ![]() находим
находим ![]() ,
,
![]() и подставляем в заданное уравнение:
и подставляем в заданное уравнение:
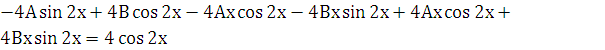 .
.
Приводя
подобные члены, приравнивая коэффициенты
при ![]() ,
,
![]() ,
получаем следующую систему:
,
получаем следующую систему: ![]() ,
отсюда
,
отсюда ![]() .
.
Окончательно
общее решение заданного уравнения имеет
вид: ![]() .
.
f(x)
 ,
где
,
где  и
и  - многочлены степени
- многочлены степени  и
и  соответственно, причем один из этих
многочленов может равняться нулю.
Укажем вид частного решения в этом
общем случае.
соответственно, причем один из этих
многочленов может равняться нулю.
Укажем вид частного решения в этом
общем случае.
Если число
 не является корнем характеристического
уравнения для уравнения (5.1), то вид
частного решения будет:
не является корнем характеристического
уравнения для уравнения (5.1), то вид
частного решения будет:
 ,
(7.2)
,
(7.2)
где
![]() – неопределенные коэффициенты, а
– неопределенные коэффициенты, а ![]() .
.
Если число
 является корнем характеристического
уравнения для уравнения (5.1) кратности
является корнем характеристического
уравнения для уравнения (5.1) кратности
 ,
то частное решение лнду будет иметь
вид:
,
то частное решение лнду будет иметь
вид:
![]() ,
(7.3)
,
(7.3)
т.е.
частное решение вида (7.2) надо умножить
на ![]() .
В выражении (7.3)
.
В выражении (7.3) ![]() - многочлены с неопределенными
коэффициентами, причем их степень
- многочлены с неопределенными
коэффициентами, причем их степень ![]() .
.
Пример 4. Указать вид частного решения для уравнения
![]() .
.
Решение.
Характеристическое
уравнение имеет вид: ![]() .
Его корни:
.
Его корни: ![]() ,
,
![]() .
Общее решение лоду имеет вид:
.
Общее решение лоду имеет вид:
![]() .
.
Правая
часть заданного уравнения имеет
специальный вид (случай 3): f(x)
![]() .
Число
.
Число ![]() является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности ![]() .
Коэффициент при
.
Коэффициент при ![]() есть многочлен первой степени, а при
есть многочлен первой степени, а при
![]() - нулевой степени, поэтому степень
многочленов с неопределенными
коэффициентами надо брать
- нулевой степени, поэтому степень
многочленов с неопределенными
коэффициентами надо брать ![]() .
Итак, вид частного решения:
.
Итак, вид частного решения:
![]() .
.
Далее
коэффициенты ![]() могут быть определены по методу
неопределенных коэффициентов.
могут быть определены по методу
неопределенных коэффициентов.
Замечание.
Если правая часть уравнения (7.1) есть
сумма двух функций f(x)
= f1(x)
+ f2(x),
где каждая из f1(x),
f2(x)
имеют специальный вид (случаи 1-3), то
частное решение ![]() подбирается в виде суммы:
подбирается в виде суммы: ![]() ,
где
,
где ![]() есть частное решение для уравнения с
правой частью f1(x),
а
есть частное решение для уравнения с
правой частью f1(x),
а ![]() есть частное решение для уравнения с
f2(x).
Аналогично находятся частные решения
в случае, когда правая часть есть
алгебраическая сумма конечного числа
функций специального вида, рассмотренного
в случаях 1-3.
есть частное решение для уравнения с
f2(x).
Аналогично находятся частные решения
в случае, когда правая часть есть
алгебраическая сумма конечного числа
функций специального вида, рассмотренного
в случаях 1-3.
