§2. Линейное однородное дифференциальное уравнение с постоянными коэффициентами.
Это уравнение имеет вид:
,
(2.1)
где
- постоянные вещественные числа. Это
уравнение имеет фундаментальную систему
решений 
,
определенную при всех 
и состоящую из степенных, показательных
и тригонометрических функций.
Соответствующее ей общее решение:
определено
в области 
,
т.е. во всем пространстве 
.
Построение
фундаментальной системы решений лоду
делается методом Эйлера, который состоит
в том, что частное решение лоду ищется
в виде 
,
где 
- некоторое число, подлежащее определению.
Подставляя эту функцию в уравнение
(2.1), после сокращения на 
получим характеристическое уравнение:
Его корни называются характеристическими числами уравнения (2.1). Различают три случая.
Все корни характеристического уравнения различны и вещественны. Обозначим их через
.
Тогда фундаментальной системой решений
будут: 
,
а общее решение имеет вид: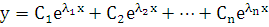 
.Все корни характеристического уравнения различны, но среди них имеются комплексные. Пусть
– комплексный корень характеристического
уравнения. Тогда 
тоже будет корнем этого уравнения. Этим
двум корням соответствуют два линейно
независимых частных решения: 
.
Записав линейно независимые частные
решения, соответствующие другим
сопряженным парам комплексных корней
и всем вещественным корням, получим
фундаментальную систему решений.
Линейная комбинация этих решений с
произвольными постоянными коэффициентами
даст общее решение уравнения (2.1).Среди корней характеристического уравнения имеются кратные. Пусть
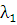- вещественный k-кратный
корень. Тогда ему соответствует 
линейно независимых частных решений
вида 
,
а в формуле общего решения – выражение
вида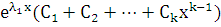 
.
Если 
- комплексный корень характеристического
уравнения кратности 
,
то ему и сопряженному с ним корню 
той же кратности соответствуют 
линейно независимых частных решений
вида:
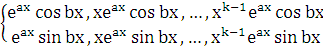
В формуле общего решения этим корнем соответствует выражение вида:
.
Записав линейно независимые частные решения указанного выше вида, соответствующие всем простым и кратным вещественным корням, а также сопряженным парам простых и кратных комплексных корней, получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными коэффициентами даст общее решение уравнения (2.1).