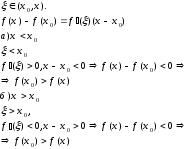11. Теорема Ролля и ее геометрический смысл. График

Если функция y=f(x) непрерывна на отрезке [a;b], дифференцируема в каждой внутренней точке этого отрезка и на его концах обращается в нуль, то внутри отрезка [a;b] найдется такая точка , что f ‘()=0.

Если функция y=f(x) удовлетворяет на отрезке [a;b] всем условиям теоремы Ролля, то на графике функции найдется такая точка, касательная в которой параллельна оси абсцисс.

12.Теорема Лагранжа и ее геометрический смысл. График

Если функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема в каждой внутренней его точке, то внутри отрезка [a;b] найдется такая точка , что выполняется равенство

f(b)-f(a)=f ‘()(b-a).

Если функция y=f(x) на отрезке [a;b] удовлетворяет всем условиям теоремы Лагранжа, то на дуге, являющейся графиком этой функции, найдется такая точка, касательная в которой будет параллельна хорде, стягивающей эту дугу.

13. Дифференциал функции. Определение.

Дифференциалом дифференцируемой функции называется главная, линейная относительно x, часть приращения функции.

Свойство инвариантности формы дифференциала.

Форма дифференциала функции f(x) не зависит от того, является ли x независимой переменной или функцией другого независимого переменного.

Док-во:

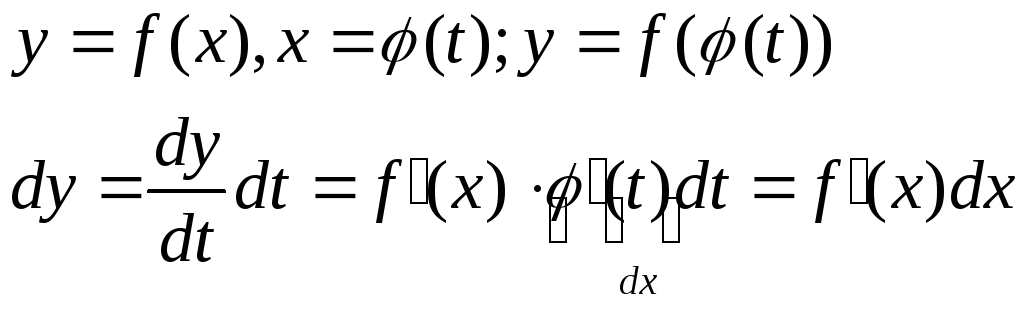
14.Геометрический смысл дифференциала.

Дифференциалом дифференцируемой функции называется главная, линейная относительно x, часть приращения функции.

Дифференциал функции в данной точке равен приращению ординаты касательной. График

15.Связь дифференцируемости с существонием производной

Для того, чтобы ф-ция y=f(x) была дифференцируемой в точке x=x₀, необходимо и достаточно, чтобы она имела в этой точке производную.

1.(15) Необходимость.

Дано: y=Ax+(x)x,

Док-ть; .

Док-во:

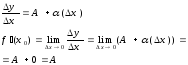
2. Достаточность.

Дано: .

Док-ть: y=Ax+(x)x,

Док-во:

∆y = ∆x·f´(∆x)+α(∆x)·∆x

16. Возрастание, убывание функции. Теорема о достаточном условии монотонности функции.

Функция y=f(x) называется возрастающей [убывающей] на интервале (a;b), если из неравенства x₂>x₁ следует неравенство f(x₂)>f(x₁) [f(x₂)<f(x₁)] при условии, что (x₁;x₂)(a;b).

Если функция y=f(x) дифференцируема на интервале (a;b) и f ‘(x)>0 [f ‘(x)<0] на этом интервале, то эта функция возрастает [убывает] на этом интервале.

Доказательство:

Возьмем две произвольные точки: x₁,x₂(a;b);

x₀(a;b), x₂>x₁.

Рассм. отрезок [x₁,x₂]. На нем функция y=f(x) удовлетворяет всем условиям теоремы Лагранжа.

По теореме Лагранжа найдется (x₁;x₂), что выполняется равенство f(x₂)-f(x₁)=f ‘()(x₂-x₁).

1) f ‘(x)>0  x₂-x₁>0 ; f ‘()>0 f(x₂)-f(x₁)>0

f(x₂)>f(x₁).

2) f ‘(x)<0

f ‘()<0

x₂-x₁>0,f(x₂)-f(x₁)<0

f(x₂)<f(x₁)

17. Определение максимума и минимума. Док-во необходимого условия экстремума.

Функция y=f(x) имеет максимум [минимум] в точке x=x₀, если найдется такая окрестность этой точки, что для всех x из этой окрестности выполняется неравенство f(x₀)>f(x) [f(x₀)<f(x)].

Если функция y=f(x) имеет в точке x=x₀ экстремум, то ее производная в этой точке равна 0 или не существует.

Дано: x=x₀ -точка максимума.

Док-ть: f ‘(x₀)=0.

Док-во:

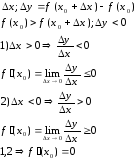
(для минимума - по аналог. док-ву)

Доказательство достаточных условий экстремума.

Если функция y=f(x) непрерывна в точке x=x₀ и дифференцируема в некоторой окрестности этой точки, и если при переходе через эту точку производная меняет знак, то в этой точке функция имеет экстремум: если знак f ‘(x) меняется с “+” на “-” - то функция имеет максимум в этой точке; если с “-” на “+” - то минимум.

Док-во:

Функция f(x) удовлетворяет всем условиям теоремы Лагранжа.