18. Определение выпуклости и вогнутости графика функции. Достаточные условия.

График функции y=f(x) называется выпуклым [вогнутым] в точке (x₀;f(x₀)), если в этой точке существует касательная к этому графику, которая в некоторой окрестности этой точки расположена выше [ниже] этой кривой.

График функции y=f(x) называется выпуклым [вогнутым] на интервале (a;b), если он выпуклый [вогнутый] в каждой точке этого интервала.

Если функция y=f(x) дважды дифференцируема на интервале (a;b) и ее вторая производная отрицательна [положительна] во всех точках этого интервала, то график функции y=f(x) является выпуклым [вогнутым] на этом интервале.

19. Определение точки перегиба. Достаточные условия.

Точка (x₀;f(x₀)) называется точкой перегиба графика функции y =f (x), если в этой точке существует касательная и если она отделяет интервал выпуклости от интервала вогнутости.

Пусть функция y=f(x) дважды дифференцируема в некоторой окрестности точки x=x₀, и в точке (x₀;f(x₀)) существует касательная к графику этой функции. Если при переходе через точку x=x₀ вторая производная меняет знак, то точка (x₀;f(x₀)) является точкой перегиба графика функции.

20.Понятие о неопределённостях(дополнение смотреть в пределах). Правило Лопиталя

Функция …..при х →a представляет собой неопределённость типа ….. ,еслипредел дан ф-ии сравен нулю Раскрыть указанную неопределённость значит вычислить предел……., если он не существует .Функция не определена при х.

Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки x=x₀ и

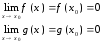
и , то выполняется равенство

21. Определение асимптоты к графику функции. Нахождение наклонной и вертикальной асимптоты.

Асимптотой данной кривой называется такая прямая, что расстояние от точки на кривой до этой прямой стремится к нулю при неограниченном удалении этой точки от начала координат.

Наклонные (невертикальные) асимптоты - асимптоты, не параллельные оси oy. Кривая, заданная уравнением y=f(x) имеет невертикальную асимптоту, определяемую уравненем y=kx+b, тогда и только тогда, когда существуют конечные пределы

Достаточные условия

и

(или соответственно при x-)

Вертикальные асимптоты - асимптоты, параллельные оси ординат. Если функция f(x) в точке x₀ имеет бесконечный разрыв, то уравнение x=x₀ есть уравнение вертикальной асимптоты графика этой функции. Для отыскания вертикальных асимптот нужно найти такие значения х = а, при приближении к которым функция y = f(x) стремится к бесконечности. Тогда прямая х = а будут вертикальной асимптотой. Условие:

Линейное векторное пространство

Линейным векторным пространством будем называть такое множество, которое подчиняется следующим условиям: для любых двух его элементов a,b, называемых векторами данного пространства введены эл-ты a+b, a, лежащие в этом же множестве, причем операции сложения и умножения на число подчинены следующим аксиомам:

1° В данном множестве существует нулевой элемент, такой что a+0=a

2° В данном множестве существует элемент -a, называемый противоположным к элементу a, такой что a+(-a)=0.

3° a+b=b+a.

4° (a+b)+c=a+(b+c)

5° Если число 1 умножить на элемент a, то получается исходный элемент: 1•a=a.

6° (a+b)= a+b.

7° (+)a=a+a.

8° (a)=()a.

Элементы a₁, ... , a_k линейного векторного пространства будем называть линейно зависимыми, если существуют такие числа ₁, ... , _k, не все одновременно равные 0, что выполняется равенство ₁a₁ + ... + _ka_k = 0.

В противном случае элементы a₁, ... , a_k называются линейно независимыми.

(Элементы a₁, ... , a_k линейного векторного пространства называются линейно независимыми, если равенство ₁a₁ + ... +_ka_k= 0 выполняется только при условии, что числа ₁, ..., _k, все равны 0.)

Элементы e₁, ... , e_n линейного векторного пространства называются его базисом, если для любого элемента a данного линейного векторного пространства существует такой набор чисел ₁, ... , _n, что справедливо равенство a=₁e₁ + ... + _ne_n.

Если в линейном векторном пространстве существует базис из n элементов, то данное пространство называется n-мерным.

Для того, чтобы элементы e₁, ... , e_n образовывали базис в неком пространстве, необходимо и достаточно, чтобы они были линейно независимы.

Если дан набор векторов, который принимается за новый базис, то матрица, составленная из этих векторов, называется матрицей перехода к новому базису и новое представление любого вектора находится по формуле

………………………………

Евклидово пространство.

Линейное векторное пространство называется евклидовым, если в нем для любых двух его элементов

……………………… и …………………… определено число, называемое скалярным произведением, обозначаемое символом

…………………………, удовлетворяющее следующим условиям:

1° ……………………………

2° ………………….

3° ………………………….

4° …………………………………

………………………….- норма (модуль) вектора

Ортогонализация базиса.

Элементы …………………….. и …………………….. евклидова пространства называются ортогональными, если их скалярное произведение равно 0.

Вектор ………………………. называется нормированным, если его длина равна 1.

Векторы ……………………… называются ортонормированными, если выполняется следующее условие: …………………

В любом n-мерном евклидовом пространстве существует ортонормированный базис.

Собственные значения и собственные и присоединенные вектора матрицы.

Число  называется собственным значением (собственным числом, точкой спектра) квадратной матрицы A, а ненулевой вектор …………………- соответствующим ему собственным вектором, если выполняется равенство (A-I)x=0 (или Ax=x).

Пусть вектор h₁ - собственный вектор, отвечающий кратному собственному значению . Тогда вектор h₂ будем называть первым присоединенным к вектору h₁, если выполнено равенство (A-I)h₂=h₁; вектор h₃ будем называть вторым присоединенным к вектору h₁, если выполнено равенство (A-I)h₃=h₂ и т. д.

Суммарно число собственных и всех присоединенных к ним векторов равно кратности собственного значения , для которого они строятся.