Вопрос №4

Теоретические сведения.

Случайной величиной называется величина, принимающая случайные значения, зависящие от ряда факторов, действия которых на исследуемую величину нельзя предусмотреть.

Полный набор значений, которые принимает случайная величина, называется генеральной совокупностью. Набор случайно отобранных из генеральной совокупности объектов называют выборочной совокупностью или выборкой. Объёмом совокупности называют число объектов в ней. При больших объёмах генеральной совокупности для обеспечения теоретических построений объём генеральной совокупности принимается равным бесконечности.

При исследовании систем массового обслуживания (СМО) широкое применение находят различные непрерывные и дискретные распределения. Первые из них описывают непрерывные случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток. Дискретные распределения соответствуют дискретным случайным величинам, возможными значениями которых являются отдельные изолированные числа, которые эта величина принимает с определенными вероятностями.

Примерами случайных непрерывных величин, с которыми приходится иметь дело в процессе исследования СМО, могут служить интервалы между моментами поступления требований в систему, время обслуживания требования и т д. Примерами дискретных случайных величин могут быть число требований, прибывающих в систему за некоторый фиксированный промежуток времени, длина очереди, число отказов в системе и т д.

Случайная величина характеризуется полностью, если указаны вероятности, с которыми она принимает то или иное значение генеральной совокупности. Вероятности могут быть описаны с помощью интегральной функции распределения F(x) или дифференциальной функции плотности распределения f(x).

Функция распределения (закон распределения) определяет вероятность (Р(x)) того, что случайная величина X принимает значение не больше заданного, т.е. F(x)=P(X<x)

Плотность распределения вероятности случайной величины X – это функция f(x) – первая производная от функции распределения F(x)

f(x)=F'(x)

Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:

Среднее значение случайной величины называется математическим ожиданием.

Дисперсия - это математическое ожидание квадрата отклонения величины x от центра её распределения m_x:

- среднее квадратическое отклонение (стандартное отклонение).

- плотность нормального распределения.

Рассмотрим основные способы моделирования непрерывных и дискретных случайных величин с заданными законами распределения.

Равномерное распределение. При моделировании случайных величин особое место занимает непрерывное распределение, называющееся равномерным. Функция плотности вероятности случайной величины, имеющей равномерное распределение на интервале (a, b), имеет вид:

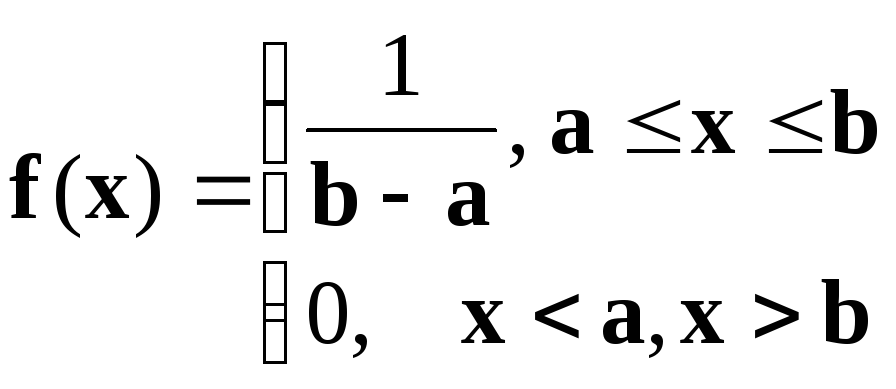(2.1)

Большинство способов моделирования случайных величин основано на использовании псевдослучайных р

Рис.1. Принцип преобразования равномерного распределения в заданное

авномерно распределенных в интервале (0,1) последовательностей чисел. При этом в основу положена следующая известная в математической статистике теорема: если случайная величина X имеет плотность распределения f(x), то распределение случайной величины Y=F(x) является равномерным в интервале (0, 1)

Таким образом, задаваясь функцией распределения F(x), можно выбирать случайное значение Y из равномерного распределения в интервале (0,1) и определять значение аргумента, для которого F(x)=Y (рис.2.1). Полученная таким образом случайная величина X будет иметь заданную функцию распределения F(x). Эта операция может быть представлена аналитически следующим выражением:

(2.2)

согласно которому определяется значение х_i, соответствующее значению функции распределения, равному y_i. Для некоторых частных законов распределения уравнение (2.2) удается решить непосредственно, в других случаях прибегают к приближенным способам решения, в частности к аппроксимации подынтегральной функции полиномами, интегрируемыми в квадратурах.

Моделирование дискретных случайных величин с известным распределением вероятностей в общем случае производится следующим образом. Предположим, что заданы численные значения вероятностей p₁, p₂, ..., p_п для независимых событий А₁, А₂, ..., А_п, составляющих полную группу. В соответствии с этим интервал (0,1) разбивается на п отрезков так, чтобы длина i-го отрезка равнялась вероятности p_i. Производя выборку случайных чисел ξ_i из равномерного распределения в интервале (0,1), будем определять, на какой отрезок попадает число ξ_i. Попадание числа на i-й отрезок фиксируется как факт свершения события А_i .

Другой способ моделирования дискретных величин состоит в формировании интервалов между моментами наступления соседних событий. При этом задача сводится к уже описанному выше случаю моделирования непрерывной случайной величины.

Экспоненциальное распределение. Непрерывная случайная функция, распределенная по экспоненциальному закону, имеет функцию распределения F(x) и плотность распределения f(x) вида:

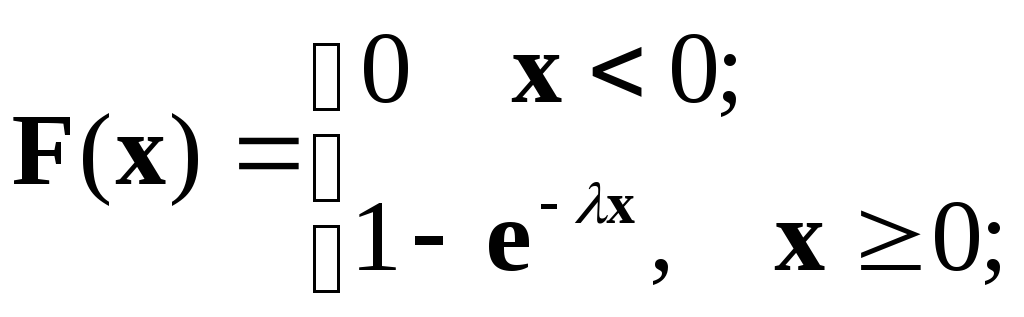(2.3)

(2.4)

Значения математического ожидания и дисперсии для экспоненциального закона распределения равны соответственно 1/λ и 1/λ².

Экспоненциальное распределение занимает в теории массового обслуживания особое место. Это связано с тем, что распределение многих величин, таких, например, как интервалы между наступлениями соседних событий, времена обслуживания и др., во многих задачах массового обслуживания принимаются имеющими экспоненциальное распределение. Хотя реальные распределения (в частности распределение времени обслуживания) часто существенно отличаются от экспоненциального, использование последнего позволяет намного упростить решение задач. Кроме того, использование экспоненциального распределения позволяет получить во многих случаях оценку для более напряженного режима обслуживания.

Рис. 2 Функция плотности и распределения для экспоненциального закона распределения

Для моделирования случайных величин x_i ,имеющих экспоненциальное распределение, можно воспользоваться непосредственным решением уравнения (2.2). Действительно, с учетом (2.4) получаем:

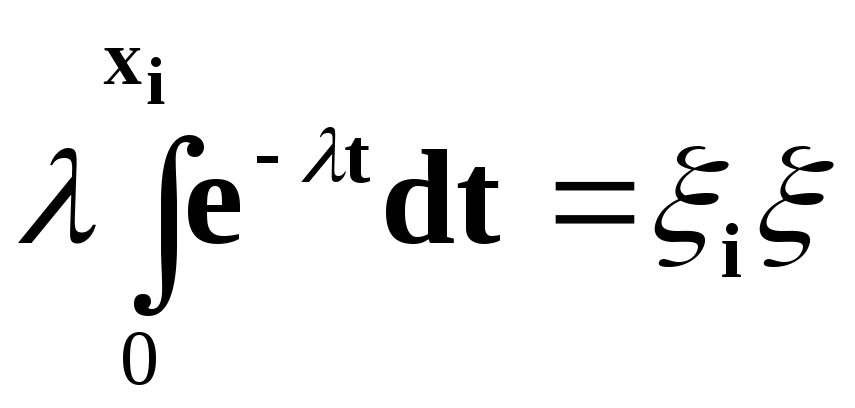(2.5)

После интегрирования имеем:

(2.6)

Поскольку случайная величина (1-_i) имеет также равномерное распределение в интервале (0,1) окончательно получаем:

x_i = -(1 / ) ln  _i = -  ln  _i (2.7)

где альтернативной параметризацией является параметр масштаба θ=1/λ).

Алгоритм формирования значений случайной величины, распределенной по экспоненциальному закону:

1. Вводятся исходные значения: количество генерируемых величин N (не менее 100) и математическое ожидание экспоненциального закона распределения (THETA);

2. Обнуляется переменная К для подсчета количества генерируемых случайных величин;

3. Генератор псевдослучайных чисел формирует число;

4. Вычисляется случайная величина по формуле 2.7;

5. Значение величины выводится на печать;

6. Значение счётчика случайных величин увеличивается на единицу;

7. Процедура формирования случайных величин повторяется до тех пор, пока не будет получено заданное количество.

Нормальное распределение. Большое число стохастических процессов описываются нормальным распределением (законом Гаусса). Этот закон, согласно теореме Ляпунова, справедлив в случаях, когда результат (исход) процесса зависит от большого числа независимых случайных факторов, каждый из которых в отдельности влияет на результат незначительно.

Нормальный закон распределения характеризуется плотностью вероятности:

(2.8)

И имеет функцию распределения:

(2.9)

Рис. 3 Функция плотности и функция распределения для нормального закона распределения вероятностей

Распределение Пуассона. Распределение Пуассона нашло очень широкое применение в теории массового обслуживания для моделирования потоков событий, поскольку оно является единственным распределением, позволяющим в большинстве случаев достаточно легко получать результаты.

Потоком событий называется последовательность событий, наступающих одно за другим в случайные моменты времени.

Поток событий называется пуассоновским если он удовлетворяет распределению Пуассона, является ординарным и не имеет последействия.

Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможными значениями являются 0,1,2, ... m ..., а вероятность того, что Х=т, выражается формулой

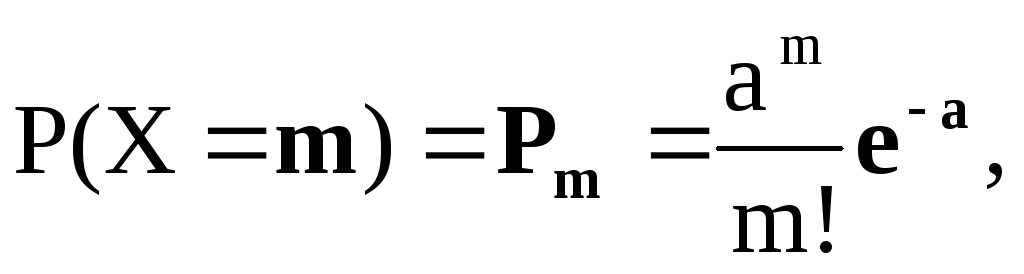(2.10)

где а>0 — параметр закона Пуассона. Для пуассоновского потока число событий, попадающих на любой участок времени (t₀ ,t₀+τ), распределения в соответствии с выражением (2.10), причем математическое ожидание числа точек, попадающих на этот участок, равно:

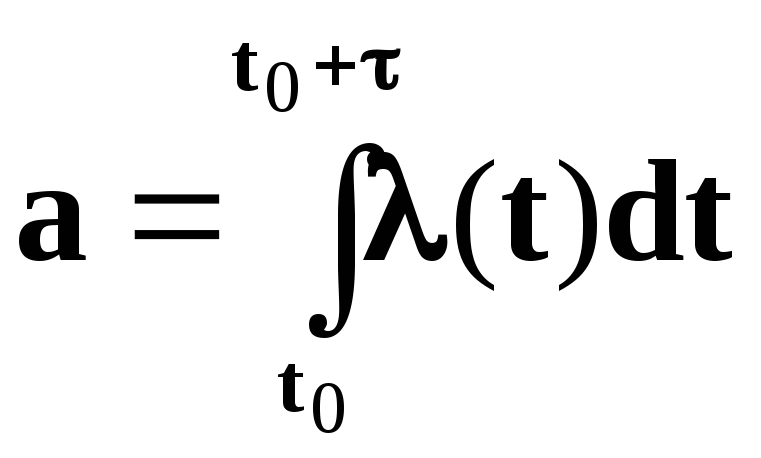(2.11)

В выражении (2.11) λ(t) есть плотность потока. В частности, если λ(t)=const, то пуассоновский поток называется стационарным пуассоновским или простейшим.

Для простейшего потока вероятность появления k событий за время т определяется законом Пуассона с параметром а= λτ, т. е.

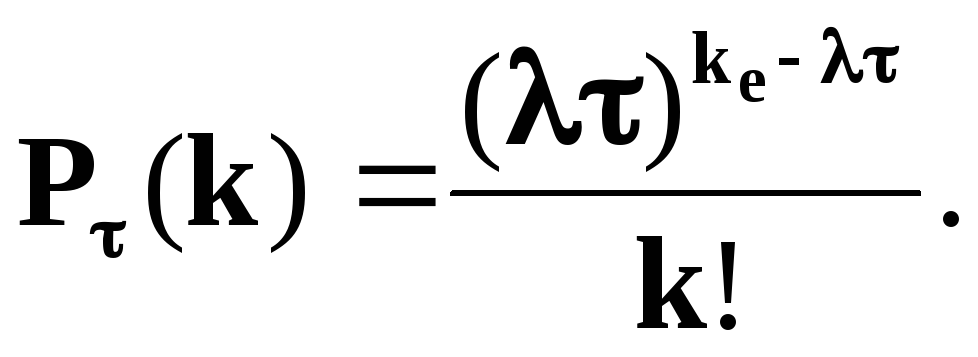(2.12)

Расстояние Т между двумя соседними событиям в простейшем потоке есть непрерывная случайная величина, распределенная по экспоненциальному закон с функцией распределения

(2.13)

Моделирование пуассоновского потока может производиться двумя способами, соответствующими выражениям (2.10) и (2.13). При первом способе в соответствии с заданными численными значениями вероятностей P₁ , Р₂, ..., Р_п независимых событий A₁ А₂, ..., А_п производится разбиение интервала (0, 1) на п отрезков так,, чтобы длина 1-го отрезка равнялась вероятности Р. Затем, выбирая из равномерного распределения в интервале (0, 1) случайные числа ξ_i определяют, на какой из отрезков попадает число ξ_i . Попадание случайного числа на i-й участок фиксируется как факт свершения события А_i.

Справочная информация по технологии работы в среде ППП EXCEL

Проведение имитационных экспериментов в среде ППП EXCEL можно осуществить путем использования инструмента "Генератор случайных чисел" дополнения "Анализ данных" (Analysis ToolPack). Если дополнение не установлено, установить его можно через меню "Сервис". Выбрать пункт "Надстройки" и поставить галочку напротив этого дополнения.

В режиме работы "Генерация случайных чисел" формируется массив случайных чисел. В зависимости от выбранного теоретического распределения меняются параметры диалогового окна Генерация случайных чисел. Общими параметрами для всех подрежимов (распределений) являются:

1. число переменных – вводится число столбцов значений, которые необходимо разместить в выходном диапазоне, если число не введено, то все столбцы будут заполнены;

2. число случайных чисел – вводится число случайных значений, которое необходимо вывести, если число не введено, то все строки будут заполнены;

3. распределение – из раскрывающегося списка выбирается тип распределения;

4. случайное рассеивание – вводится стартовое число для генерации определенной последовательности СЧ;

5. выходной интервал.

Строить графики дифференциальных и интегральных функций распределения удобно с помощью мастера диаграмм. Для этого необходимо предварительно сформировать интегральные и дифференциальные массивы значений, для этого использовать функцию, соответствующую выбранному распределению, используя в качестве её аргументов сгенерированную последовательность СЧ.

Пример

Для закупки и последующей реализации мужских курток фирмой было проведено выборочное обследование мужского населения города в возрасте от 18 до 65 лет в целях определения его среднего роста. В результате было установлено, что средний рост 176 см, стандартное отклонение 6 см. Необходимо определить, какой процент общего числа закупаемых курток должны составлять куртки пятого роста (182-186 см). Предполагается что рост мужского населения распределен по нормальному закону. Построить графики функции и плотности распределения

Решение

Сначала в MS Excel последовательность случайных чисел. Для этого:

1. вызовем из меню Сервис команду Анализ данных→Генерация случайных чисел.

2. Заполним диалоговое окно как показано на рис.4.

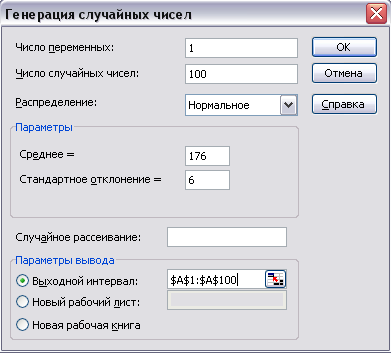
Рис.4.

После нажимаем кнопку OK и в указанном нами диапазоне получаем последовательность псевдослучайных чисел.

3. Упорядочиваем их по возрастанию.

4. Для подсчета значений функции плотности нормального распределения используем функцию НОРМРАСП с аргументом интегральная=0. Таким образом, по формуле представленной на рис. 5 для числа x=154,6192 из ячейки А1 получим значение = 0,000116

Рис.5.

5. Значения функции распределения считаем используя функцию НОРМРАСП с аргументом интегральная=1. Таким образом, по формуле представленной на рис. 6 для числа x=154,6192 из ячейки А1 получим значение = 0,000183

Рис.6.

6. Решаем задачу по формуле:

=НОРМРАСП(186;176;6;1)-НОРМРАСП(182;176;6;1)=0,949675-0,84109=10,858≈11%

Вывод: куртки 5-го роста должны составлять приблизительно 11% от общего числа закупаемых курток.

7. Строим графики полученных функций, используя мастер диаграмм. Выделяем диапазон ячеек А1:С100 и вызываем мастер диаграмм.

8. На первом шаге выбираем тип диаграммы – точечная, вид – со сглаживающими линиями без маркеров.

9. На втором шаге проверяем правильность выбранного диапазона данных.

10. Указываем параметры диаграммы на третьем шаге и расположение на четвертом. Нажимаем кнопку Готово. Получаем результат (рис.7)

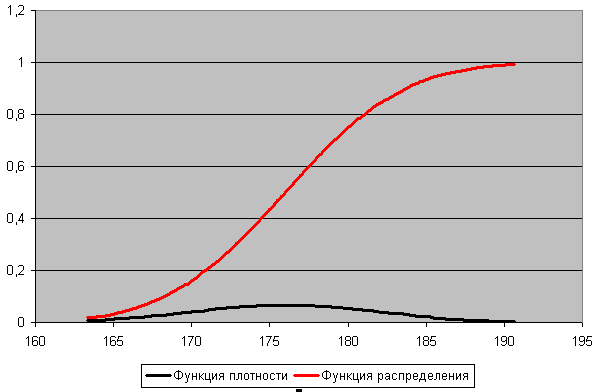
Рис.7.

8