ГОСЫ Методы вычислений 18 стр Январь 2012

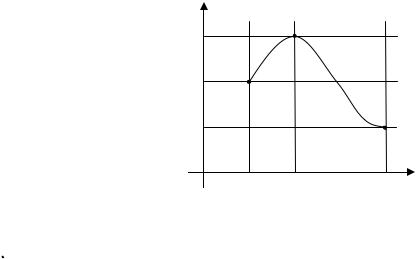
4. Интерполяционный многочлен Лагранжа. Погрешность многочлена (без вывода).

.

! # ! $

f ( x) n + 1 ! :

x0 , x1, K, xn

–

!

f ( x) – #

! #

f0 , f1, K, fn

–

!

f ( xi ) = fi , i = 0, n – ! #

f1

f0

fn

x0

x1

xn

: & ## f ( x)

# n

!,

!

! # # ! # !

f ( x) = Ln (x) : Ln (xi ) = fi ,

i = 0, n (( & # n).

! #

.

L ( x) = a

+ a x + a

x2 + L+ a

xn

(1) – n-$ #. %- &

n

0

1

2

n

# #:

2

n

y0 = Ln ( x0 ) = a0 + a1x0 + a2 x0

+ L + an x0

y = L ( x ) = a

+ a x + a

x2 + L + a xn

1

n

1

0

1 1

2 1

n 1

(2)

LLLLLLLLLLLLLLLLL

2

n

yn = Ln ( xn ) = a0

+ a1xn + a2 xn

+ L + an xn

4 - $ # # – *

x

x

2

L xn

1

0

0

0

1

x

x

2

L xn

= ∏(xi − x j ) ≠ 0

1

1

1

L L L L L

0≤ j <i ≤n

1

x

x

2

L xn

n

n

n

, # x j !. 0, # # (2) "

# ( %). ! # ' # # #

(1). .# # & - ai # ' (

" - $ # # ! & " n ( , n = 20).

# , " ( # #.

11

# :

		n
	Ln ( x) = ∑ fi li ( x)		(3) ,
		i =0
li ( x) – n- $ # $,
		0, #i ≠ j	(4)
li	( x j	) =
		1, #i = j	(5)

* ! li ( x) & ( ! .

! # (4) #,

li ( x) = A( x − x0 )K( x − xi −1 )( x − xi +1 )K( x − xn )

6 ! # (5)

1

A =

( xi − x0 )K( xi − xi −1 )( xi − xi +1 )K( xi − xn )

	n	x	− x j
	4 #( li (x) = ∏
		x	− x
	j =0			j
		i

j≠i

, :

n

n

x

− x j

∑ fi

∏

x

− x

i=0

j=0

j

i

j≠i

! % ( )

f(x) = Ln(x)

f(x) = Ln(x) + Rn(x), Rn(x) – " #

Rn

( x) = f ( x) − Ln

( x) =

f ( n +1) (c)

ωn ( x),

Rn ( x)

≤

M n +1

ωn ( x)

, ωn ( x) = ( x − x0 )K( x −xn )

(n + 1)!

(n + 1)!

12

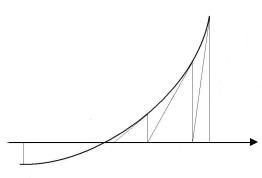
5. Решение нелинейных алгебраических уравнений методом хорд и методом Ньютона. Геометрическая интерпретация методов. Оценка погрешности.

.

# ! f ( x) . , # $ #

f ( x) = 0 . % – - #, # , # ' #

& # ξ : f (ξ ) ≡ 0 . ε – # " !, ! # ( ε << 1)

! # # !.

1)## #, # & $. . $ !,

( (! ! $);

2). - !, # ' # #$ , $

& ! # $ # (.

.

% ' # $# , ! # # !$ f ( x) . # # # ! ! !, & - ! # ' #, "$ , . & #

y = f ( x) # $ # # # ( # ##. # #

& ! $. # !

- p( x) = t( x) , y = p( x) y = t ( x) (

# & . 6 # ## # - #

. & ! $ ( ! .

1. * + ( #) y = f(x)

a ξ x3 x2 x1 b=x0

x0 – &

4 (x0, f(x0)).

- $ # (. #$ x0: y = f′(x0)· (x – x0) + f(x0).

. ! - # #$ # # ( # ## – (x1, 0):

x1 = x0 −	f ( x0 )
		.
	f ′( x0 )

4 (x1, f(x1)). - $ # (. . .

= x

−

f ( xn )

< ε .

!"#:

x

n+1

n

, # #:

f (x

)

f ′( xn )

n+1

0 # # # . ( .

− ξ

≤

f ( xn )

f ′( x)

≥ m [a, b] (!

f (x ) − f (ξ )

=

f ′(Θ)

x − fξ

4 " #

x

n

,

).

m

n

n

13

2. % ! * +.

$ ! ( # , & " (

# (, # ' (, ( #$, $ ". y = f(x)

a ξ x3 x2 x1 b=x0

	:	xn +1	= xn	−	f ( xn )
					f ′( x0 )

* - & # &$ ! ! (, # # &,

.

3.#

* . ( # # ! ( , # . & ! # ( $, ! $ &.

y = f(x)

x2	x3 x4
a=x1	ξ	b=x0

4 (x0, f(x0)) (x1, f(x1))

! - . $, '$ ! x0 x1:

x − x1	=	y − f ( x1 )	, f(x0)· f′′(x0) > 0 – # $ .
		f ( x0 ) − f ( x1)
x0 − x1

. ! - # # # ( # ## – (x2, 0):

	= x1	−	f ( x1 ) ( x0	− x1 )
x2					.
			f ( x0 ) − f ( x1 )

4 (x2, f(x2)). # (x0, f(x0)) (x2, f(x2)). . .

:

x

= x −

f ( xn ) ( xn − x0 )

, # #:

f (x

)

< ε .

n+1

n

f ( xn ) − f ( x0 )

n+1

0 # # # # # # #$ ##.

4 " #

x

n

− ξ

≤

f ( xn )

,

f ′( x)

≥ m [a, b] .

m

14

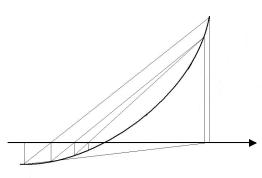
4. % ! #.

# ! # '$, # # # ,

& . 0 # # # - ", , ",

. (.

y = f(x)

x2	x4 x5	x3
a=x1	ξ	b=x0

:	xn+1 = xn	−	f ( xn ) ( xn − xn −1 )
			f ( xn ) − f ( xn−1)

, !, ## :

1)% #$ & ( . ();

2)& $ ! &.

# # # # 1-4. #:

1)	/ f ( x) & [a, b] ;
2)	. ! [a, b] # ' # #$ f ( x) = 0 ( f (a) f (b) < 0) ;
3)	! f ′( x), f ′′( x) # ( ! [a, b] ' ( # 0;
4)	. & x0	# f ( x0 ) f ′′( x0 ) > 0 .
, ! # #		( f ( x) = 0 .

15

6. Метод простой итерации решения систем линейных алгебраических уравнений. Условия сходимости метода.

* .

! ## # . # # -# x = ( x1 , K, xn )T . . x – - #, (' # ('

#:

1. x ≥ 0, x = 0 x = 0 ;

2.αx = α x ;

3. x + y ≤ x + y .

, ## #

n

1.

x

1 =

x1

+ L +

xn

= ∑

xi

;

i =1

n

2.

= x12

+ L + xn2

=

∑xi2

;

x

2

i =1

3.x ∞ = max xi .

i =1, n

* !.

# # # x = ( x1 , K, xn )T x , # #$ # $ $

# #	A = (aij )m x n ! (		A		= sup			Ax			–
								x
					x ≠0
(# #	# $ ).

. A – - #, (' # (' #: 1. A ≥ 0, A = 0 A = 0 ;

2.αA = α A ;

3. A + B ≤ A + B ;

4. Ax ≤ A x ;

5. A B ≤ A B ;

0 # # # # # #

m

1.A = max ∑ aij – # ! # $ #;

1 1≤ j ≤ n i =1

2. A 2 = max λ (AT A) , λ – # # # ATA;

n

3. A ∞ = max1≤i ≤m ∑ aij – # ! # $ #.

j =1

16

.

# # n $ # $ # n ! #:

			a x		+ a x		+ K + a x				= b
			11 1		12 2		1n n				1
			a	x	+ a	x	+ K + a		x		= b
				21 1		22 2		2n n			2
			LLLLLLLLLLLL
			a	x	+ a	x	+ K + a		x		= b
				n1 1		n 2 2		nn n			n
										≠ 0 . ) " # # #
# # # # # ", #									A
ξ = (ξ , K, ξ		n	)T , # # #, # ' # & #.
1
0 # $ :
					Ax = b (1) ,
A = (aij )n x n	– -

b= (b1 , K, bn )T – # #

x = ( x1 , K, xn )T – # ! #

, # & " # # ! # " # $

# (.

! (,-.

. & # # (1) # # #

x = Bx + c (2)

B = (b )	n x n	, c = (c , K, c )T ,		x = ( x , K, x )T		,
ij		1	n	1	n

(1) → (2) & # ! # #, :

Ax = b

x= x + F ( Ax − b)

x= x + FAx − Fb

x= (E + FA) x − Fb

14243 {

			B	c
F – !	& .
		& ' !
. & " x = Bx + c . * ( & x(0) = (x(0)					,K, x(0) )T	. .
				1	n
# (' & x(1) = Bx( 0) + c, x( 2) = Bx(1) + c, K.
:		x( n +1) = Bx( n) + c	.

0 # ! # x( 0) . # B " , (

& x( 0) #$# ξ.

17

' # !.

# B < 1 ( & x( 0) #$ " # #

$ # $ # # " ( # #.

:

x = Bx + c,

B

< 1 – # # (2)

ξ = (ξ , K, ξ

n

)T

– " , # ξ ≡ Bξ + c

1

x( n +1) = Bx( n) + c

. & !: x( 0) : lim x( n ) = ξ, (x( n ) → ξ), #

x( n) − ξ

→ 0

n →∞

n →∞

n→∞

$% ": ) ## ! #

x( n) − ξ = (Bx( n −1) + c) − (Bξ + c) = B( x( n −1) − ξ ) ≤ B x( n −1) − ξ =

= B(Bx( n − 2) + c) − (Bξ + c) = B B( x( n − 2) − ξ ) ≤ B 2 x( n − 2) − ξ =

= L ≤ B n x( 0) − ξ → 0, ( B < 1)

n →∞

& & " # #$ .

x( n) − ξ = (Bx( n −1) + c) − (Bξ + c) = Bx( n −1) − Bξ = Bx( n −1) − Bξ + Bx( n) − Bx( n) ≤

≤ Bx( n −1) − Bx( n) + Bx( n) − Bξ ≤ B x( n) − x( n −1) + B x( n ) − ξ

) ! " - # #

x( n)

− ξ

,

B

< 1

x( n) − ξ

≤

B

x( n) − x( n −1)

1 −

B

. # - $ # ' # # ! ## # "

# # ( ε:

x( n +1) − x( n ) ≤ 1 − B ε

B

18