ПП _07 _Законы распр и числ хар

ПП 7. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ХАРАКТЕРИСТИКИ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

Случайная величина (с.в.) Х в результате опыта принимает то или иное значение {X = x1}, {X = x2}, …, {X = xn}….

Множество {xi },(i =1,2,...,n,...)– множество возможных значений с.в.

С.в. Х – функция элементарного события: Х=ϕ (ω), где ω Ω. Множество {xi } возможных значений с.в. Х состоит из всех значений, которые принимает

функция ϕ (ω).

С.в. называется дискретной, если множество {xi } – конечно или счетно (образует конечный или бесконечный ряд чисел) и непрерывной, если множество {xi } – несчетно (значения с.в. заполняют конечный или бесконечный про-

межуток числовой оси).

Закон распределения (ряд распределения) д.с.в. задается в виде таблицы:

	X		x1	x2	x3		…		xn
	P		p1	p2	p3		…		pn
где xi , (i =1,2,...,n,...)		– возможные значения с.в.					X ,
pi = P(X = xi ) – вероятность того, что в резуль-
тате опыта с.в.	X примет						Pi
	n
значение xi ,	∑pi =1.
	i=1
Многоугольник (полигон) распределения -
множество точек Mi (xi ; pi ), (i =1,2,...,n,...).							0		1 2 3 xi

7.1. Функция распределения с.в.

Функцией распределения с.в. X называется вероятность того, что с.в. X примет значение меньшее, чем заданное х, F (x)= P(X < x), −∞ < x < ∞ .

1. F (x2 )≥ F (x1 ) при x2 > x1 ;

2. F (−∞)= lim F (x)= 0 ;

x→−∞

3. F (+∞)= lim F (x)=1.

x→+∞

Функция распределения дискретной случайной величины

Ряд распределения дискретной с.в.:

X

0

1

2

3

P

0,24

0,46

0,26

0,04

Найдем F (x):

•

если x ≤ 0,

то F (x)= 0 ;

•

если 0 < x ≤1, то F (x)= P (X = 0)= 0, 24 ;

•

если 1 < x ≤ 2 , то

F (x)= P (X < x)= P (X = 0)+ P (X =1)= 0, 24 +0, 46 = 0,70;

•

если2 < x ≤ 3, то

F (x)= P (

X = 0)+ P (X =1)+ P(X = 2)= 0, 24 +0, 46 +0, 26 = 0,96 ;

•

если x > 3, то F (x)= P (X = 0)+ P (X =1)+ P (X = 2)+ P (X = 3)=1.

Функция распределения непрерывной случайной величины

F (x)= P{X < x} = ∫x f (x)dx ,

−∞

f (x) – плотность распределения с.в. X ,

ƒ(x)≥0,	∞∫ f (x)dx =1.
	−∞

P{α < X < β}= P{X < β}− P{X <α}= F

.

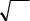
7.2. Числовые характеристики случайных величин

1. Математическое ожидание

Математическим ожиданием (средним значением случайной величины)

дискретной с.в. называется сумма произведений всех возможных ее значений на вероятности этих значений.

M(X )= ∑xi pi = mx

i=1n

1.M (c) = c , с - константа;

2.M (cX )= cM (X );

3.M (X ±Y ) = M (X )± M (Y );

4.M (X − M (X ))= 0 ;

5.M (X Y )= M (X ) M (Y ), ( X , Y - независимые с.в.).

Математическим ожиданием непрерывной с.в. Х с плотностью ƒ(х) назы-

вается величина mx = M (X )= ∞∫ x f (x)dx .

−∞

2. Дисперсия. Среднее квадратическое отклонение

Дисперсией D(x) = Dx с.в. Х называется Dx= M ((X – Mx)2),

разность X – Mx называется отклонением с.в. Х от ее математического ожидания.

n

Для дискретной с.в.: Dx = ∑( xi − mx )2 pi ,

i=1

для непрерывной с.в.: Dx = ∞∫(x − mx )2 f ( x )dx .

−∞

Dx = M ((X −Mx )2 )= M (X 2 )− M x2 .

1.D(X )≥ 0 ;

2.D(c)= 0 ;

3.D(cX )= c2 D(X );

4.D(X +Y )= D(X )+ D(Y ), ( X , Y - независимые с.в.);

5.D(X +c)= D(X ).

3.Среднее квадратическое отклонение (с.к.о.) с.в:

Dx =σx .

4. Стандартной случайной величиной, соответствующей случайной ве-

личине X называется случайная величина Y =

X − MX

.

σx

X − MX

MX − MX = 0 ,

X − MX

DX

MY = M

=

DY = D

=

=1.

σx

σx

(σx )

2

σx

5. Мода, медиана, квантили

Мода Мoх дискретной с.в. – это наиболее вероятное значение с.в.; для непрерывной с.в. – это точка максимума плотности распределения.

Медиана Мeх с.в. - это такое значение непрерывной с.в., для которого

P{X < xm}= P{X > xm}= 12 .

Если плотность распределения симметрична относительно прямой x = a и распределение одномодально, то:

M (X )= Mex = Mox .

Квантилью уровня p qp с.в. X называется решение уравнения F (qp )= p , где F (x) – функция распределения с.в. X , p – некоторое число,

0 < p <1.

Медиана распределения является квантилью уровня 0,5: Mex = q0,5 .

6. Моменты случайных величин

Начальным моментом k-ого порядка с.в. X называется число αk (X ), рав-

ное математическому ожиданию k-й степени этой величины, X k :
	αk (X )= M (X k ).
n	∞
αk (X )= ∑xik pi , αk (X )= ∫ xk f (x)dx – для дискретной и непрерывной
i=1	−∞

с.в. соответственно. При k =1, то M (X )=α1 (X ).

ο

Центрированной случайной величиной X называется отклонение слу-

ο

чайной величины от ее математического ожидания: X = X −mx .

Центрирование случайной величины означает перенос начала координат

в точку mx .

Центральными моментами называются моменты центрированной слу-

чайной величины (аналог моментов относительно центра массы в механике). Центральным моментом порядка k с.в. X называется величина

	ο k		k	).
µk (X )= M X			= M ((X −mx )

n

k

∞

µk

= ∑(xi −mx )

pi ,

µs = ∫(x −mx )k

f (x)dx – для дискретной и непрерыв-

i=1

−∞

ной с.в. соответственно.

Абсолютные моменты (начальные и центральные):

k

(X )= M

(

k

)

k

(X )

ο

k

(

x

k

)

β

X

, ν

= M

X

= M

X −m

.

Связь между начальными и центральными моментами

µ = M

X = M (X − m )= 0 .

ο

1

x

µ2

= M

ο 2

= α2 − mx2

µ2 = Dx .

X

µ

= M

D

=

α

−3α m

+

2m3 .

3

X 3

3

x

2

x

7. «правило трех сигм»

Значения случайной величины Х с

3σx

3σx

вероятностью, близкой к 1, не выходят

за пределы интервала mx

±3σx .

mx

Если многоугольник

распределения дискретной случайной величины или плотность распределения непрерывной случайной величины

симметричны относительно прямой x = mx , то все центральные моменты нечетного порядка µ2k +1 = 0, k =1,2,... равны нулю.

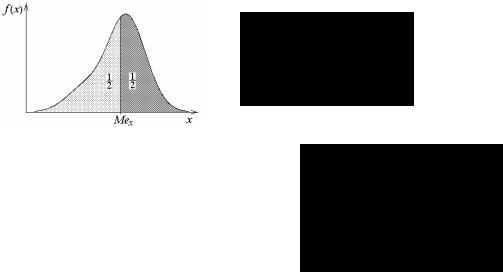
8. Коэффициент асимметрии

As = Sk = µ3 .

σx3

I – кривая с положительной асимметрией, As >0 ,

II – с отрицательной асимметрией, As < 0 .

9. Эксцесс					ε	x	=		µ4	−3.
								σ4
									x
		Эксцесс нормального распределения равен
ε	x	= 0 ,	µ4	= 3 .
		σ4
			x

7.3.Основные законы распределения случайных величин

иих числовые характеристики

7.3.1. Законы распределения дискретной с.в.

1. Биномиальное распределение:

P (X = k) =Ck pk (1− p)n−k , 0 < p <1, k = 0,1,2,...n

n

n

n!

k

Cn

=

.

k !(n −k )!

M (X i )= p , D (Xi )= pq .

n

n

σ (X )= npq .

M

∑Xi = np , D

∑Xi

= npq ,

i=1

i=1

X

X

pq

X

=

pq

M

=

p , D

=

, σ

.

n

n

n

n

n

2. Распределение Пуассона (предельный случай биномиального распределения

при n→∞, р→0, lim(np) = λ = const , описывает так называемый поток собы-

n→∞

тий):

P (X = k )= λk e−λ . ∑∞ P (X = k )=1, k = 0,1,2,....

k! k =0

M (X )= D (X )= λ , λ – среднее количество событий за определенный

промежуток времени (средняя интенсивность потока).

Ниже приведены вероятности для различных значений k при некоторых значениях λ. Смысл имеют значения функций только при целых x .

3.Распределение Паскаля:

P(n, p,m) =Cn+ − pm (1− p)n

m n 1

−вероятность того, что до появления события А m раз оно не появится n раз. 4. Геометрическое распределение (частный случай распределения Паскаля):

Pn ( X = k) = p (1− p)k , 0 < p <1, k =1,2,3,.....

−вероятность появления события А в первый раз после точно k испытаний.

	m		= 1 − p		; D =	1 − p .
		x	p		x	p2
5. Гипергеометрическое распределение:
P ( X = k) =	CMk		CNn−−kM		, k = 0,1,2,...,min (M,n).
			CNn
n

7.3. Законы распределения непрерывной с.в.

1. Равномерное распределение:

	0,		x ≤ a и x > b,
f (x) =
	1			, при a < x ≤ b
	b - a

−∞< a <b <∞

График функции распределения:

0, при x ≤ a,

F (x) = x - a , при a < x ≤ b ,b - a

1, при x>b.

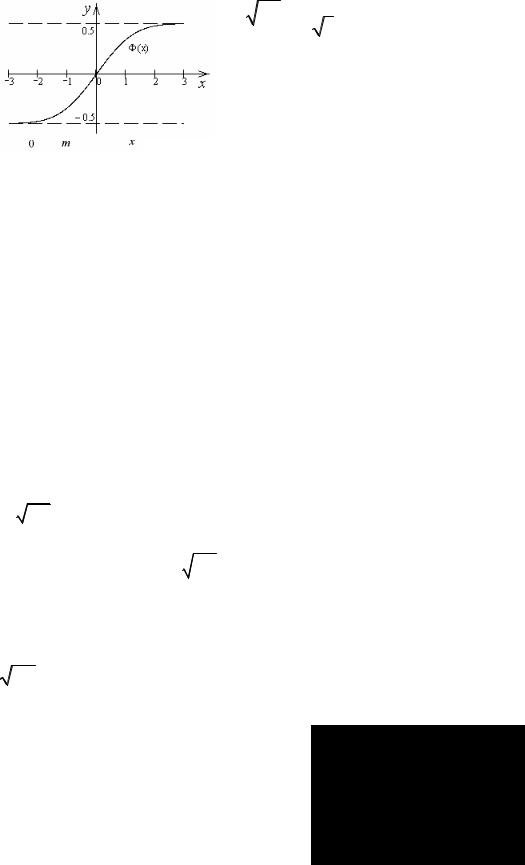
x

x2 − x1

P{x1 < X < x2}= ∫2

f ( x )dx =

.

x1

b − a

m

x

=

a +b

= Me

,

D

x

=

(b − a)2

, σ

x

=

D

=

b − a

. Мода отсутствует.

2

x

12

x

2

3

µ3 = 0, коэффициент асимметрии Sk = 0, µ4

= ( b − a )4

;

µ4

80

эксцесс ε

x

=

−3 = −1,2 < 0 .

σx4

2. Показательное (экспоненциальное)

распреде-

ление – аналог закона Пуассона для непрерывных

с.в.:

−λx

f (x) =

λe

, x ≥ 0,

x < 0,

0,

λ > 0 - параметр распределения.

Функция распределения F(x):

.

−λx

F(x) =

1−e

, x ≥ 0,

0,

1

x < 0.

1

2

µ3

m

=σ

=

; D =

, µ

=

, Sk =

= 2 > 0 .

x

x

λ

x

λ2

3

λ3

σ3

x

3. Нормальное распределение (распределение Гаусса) N (m,σ ):

f ( x ) =

1

e−

(x−m)2

2σ2

σ

2π

m,σ - параметры распределения, они равны

m= Мех=Moх=m, σ =

Dx .

µ4

= 3 , ε

x

=

µ4

−3 = 0

σ

4

σ

4

x

x

1

x

t2

Ф(x) =

∫e− 2 dt

- функция Лапласа (специ-

2π

0

альные таблицы).

β − m) −Ф(α − m) .

P{α < X < β} =Ф(

σ

σ

Свойства функции Лапласа:

1)Ф(0)= 0 ,

2)Ф(−x)= −Ф(x) (нечетная),

3)Ф(∞)= 0,5.

F (x)= P(X < x)= P(−∞< X < x)= 1 +Ф х−m 2 σ

{	Ф	(		)	}
α = −∞, β = х,			−∞		= −0,5 .

Вероятность того, что величина отклонения меньше δ > 0 :

P(

X −m

δ

, при m = 0:

P(

X

δ

<δ )= 2Ф

<δ )= 2Ф

.

σ

σ

4. Гамма – распределение.

Тесно связано с нормальным так называемое Γα ,λ распределение с плотно-

стью

f (x)= Γα(λλ )xλ−1e−x , x ≥ 0.

Здесь α > 0 , λ > 0 – параметры, Γ(λ)= ∞∫xλ−1e−xdx – гамма-функция Эйлера;

0

при λ > 0 Γ(λ +1)= λΓ(λ) (аналог факториала, (n +1)! =(n +1)n!).

Распределение χ2 (хи-квадрат).

Пусть независимые случайные величины Xi распределены по нормальному закону с M (Xi )= ai и средними квадратическими отклонениями σi ,

i =1,...,n . Для каждой из этих случайных величин образуем стандартизованную случайную величину

W =

Xi

−ai

,

i =1,...,n .

i

σi

Сумма квадратов стандартизованных переменных

2

χ

2

=W

2

+W

2

+ ...+W

2

=

X

1

− a

2

+

X

2

− a

2

2

+ ...+

X

n

− a

n

1

n

1

2

n

σ1

σ2

σn

называется случайной величиной, распределенной по закону χ2

сν = n сте-

пенями свободы. Плотность распределения этой величины связана с гамма-

распределением: χn2 =Γ1

,

n ,

2

2

α

λ

ν

χ2

f (χ2 )=

(χ2 )

−1 e−

.

2

2

ν

ν

22 Γ

2

На практике, как правило, используются квантили χ2 -распределения χα2 ,ν . Квантиль χα2 ,ν , соответствующий заданному уровню вероятности α – решение

(

α ,ν )

∞

(

) (

)

уравнения P

χ2

=

∫

f

χ2

χ2

=α .

> χ2

d

χ

2

α ,ν

Распределение Стьюдента ( t -распределение).

Пусть Wi , i =1,...,n

– стандартные случайные величины, распределенные

по закону N (0,1). Распределение случайной величины

tn =

W

=

W

1 χn2

1 ∑Wi

n

n i=1

n

называется распределением Стьюдента с n степенями свободы.

Плотность распределения

ν +1

Γ

ν +1

+ t

2

−

2

f (t )= S (t,ν )=

2

1

,

ν

ν

πνΓ

2

M (t )= 0 ,

D(t )=

n

(n > 2).

n

− 2

Это распределение широко используется при статистических вычислениях. При увеличении числа степеней свободы t -распределение приближается к

стандартному нормальному N (0,1). На практике используются квантили t -

распределения tα

,ν

. Квантиль tα

, соответствующий заданному уровню веро-

2

2

,ν

α

∞

(

)

∫

ятности α – решение уравнения P

t

> t

= 2

f

t dt =α .

2 ,ν

tα

,ν

2

ПП 7.1. Числовые характеристики случайных величин

№ п/п Задание

Ответ

Вероятность попадания стрелком в мишень равна 23 .

Стрелок сделал 15 выстрелов. Случайная величина X − число попаданий в мишень. Найдите числовые характеристики (моду, математическое ожидание, дисперсию, ПП СКО) числа попаданий и вероятность того, что случайная

7.№1. величина X примет значение, отличающееся от математического ожидания не более чем на СКО.

РЕШЕНИЕ:

Интересующая нас величина распределена по биномиальному закону: Pn (X = k) =Cnk pk (1− p)n−k .