ПП _02 _Алгебра событий_Классическое опр вер

ПП2. СЛУЧАЙНЫЕ СОБЫТИЯ И ОПЕРАЦИИ НАД НИМИ КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Событие ─ исход наблюдения или эксперимента. Когда оно при реализации некоторой совокупности условий может произойти, а может и не произой-

ти, получаем случайное событие.

1. Пространство элементарных событий (исходов опыта)

Рассмотрим какой-нибудь идеализированный опыт. Каждый исход этого опыта представляется одним и только одним элементарным событием.

Совокупность всех элементарных исходов опыта образует пространство Ω элементарных событий. Любое случайное событие A , связанное с этим опытом, можно рассматривать как подпространство благоприятствующих этому событию элементарных событий пространства Ω.

С конкретным опытом можно связать невозможное и достоверное Ω события.

Пространство элементарных событий называется дискретным, если оно состоит лишь из конечного числа точек (исходов) или из бесконечного числа точек, которые могут быть занумерованы в простую последовательность.

Примеры соотношений между событиями в терминах теории множеств:

1)A B или B A : { A влечет за собой B } или { B является следствием A } означает, что если произошло событие A , то тем самым произошло и В;

2)C = A + B : {произошло или A , или B , или и то и другое вместе}.

	Событие С является объединением ( ) или суммой (+) событий A и B и
	состоит в наступлении хотя бы одного их них.
	A + B = B + A ,
	(A + B)+C = A +(B +C );
3)	C = A B : {произошло и A , и B }.
	Событие C является пересечением ( ∩) или произведением ( ) событий
	A и B , состоит в их одновременном наступлении.
	Если одно из событий A или B не произойдет, то не произойдет и C ;
4)	Два события A и B , пересечение которых ─ невозможное событие
	(A B =), называются несовместными.
	Объединением двух несовместных событий A и B называется событие C ,
	заключающееся в появлении либо события A , либо события B ;
5)	Два события A и B называются совместными, когда существует хотя бы
	одно элементарное событие, благоприятствующее и событию A ,
	и событию B .
6)	Если объединение событий A и B ─ достоверное событие (A + B =Ω),

а пересечение (A B =) ─ невозможное событие, то события A и B на-

зываются противоположными: A = B и B = A .

1

A A = A ,

A B = B A ,

A (B C )=(A B) C ,

A B = A B .

Все вышеизложенное крайне важно для вычисления вероятности событий!

ПП 2.1. Алгебра событий

№ п/п	Задание	Ответ
	Монета подбрасывается три раза. Наблюдаемый резуль-
	тат – появление герба Г или цифры Ц на верхней сторо-
	не монеты. Постройте множество элементарных исхо-
	дов Ω опыта и множества элементарных исходов, соот-
	ветствующих указанным событиям (подмножествам ис-
	ходного опыта):
	А {герб выпал ровно один раз};
ПП 2.1.	B {ни разу не выпала цифра};
	C {выпало больше гербов, чем цифр};
№1
	D {герб выпал не менее, чем два раза подряд}.
	РЕШЕНИЕ:
	Ω= {ГГГ, ГГЦ, ГЦГ, ГЦЦ, ЦГГ, ЦГЦ, ЦЦГ, ЦЦЦ};
	А {ЦЦ, ЦГЦ, ЦЦГ};
	В {ГГГ};
	С {ГГЦ, ГГГ, ЦГГ, ГЦГ};
	D {ГГЦ, ГГГ, ЦГГ}.
ПП 2.1.	Какие из событий:
№2	А {попадание в мишень первым выстрелом},
	B {попадание в мишень по крайней мере одним из че-
	тыре выстрелов},
	C {попадание точно в мишень одним из 2 выстрелов},
	D {попадание в мишень не более чем 5 выстрелами}
	являются частью другого события?
	РЕШЕНИЕ:
	A C B D
ПП 2.1.	В чем состоит событие ( A + B ), для событий
№3	А {появление двух гербов при подбрасывании двух мо-
	нет} и
	B {появление герба и цифры при подбрасывании двух
	монет}?
	РЕШЕНИЕ:
	( A + B ) {появление хотя бы одного герба при подбрасы-
	вании двух монет}.

2

ПП 2.1.	В чем состоит событие ( A + B +C ) для событий
№4	А {появление 6 очков при бросании игральной кости},
	B {появление 5 очков при бросании игральной кости},
	С {появление 4 очков при бросании игральной кости}?
	РЕШЕНИЕ:

(A + B +C ) {появилось не меньше 4 очков}.

ПП2.1. Наугад отобранная деталь может оказаться первого сор- №5 та (событие А), или второго (событие В), или третьего

(событие С).

В чем состоят события A + B , A +C , A C , (A B)+C ?

Выполняется ли равенство

A

В

=

А В

?

РЕШЕНИЕ:

A + B {деталь либо первого, либо 2 сорта},

{деталь 2 сорта},

A +C

A C =,

(A B)+C = +C =C .

Нет, C ≠ Ω.

ПП 2.1.

Пусть А, В и С ─ случайные события, которые являются

№6

элементарными событиями одного и того же простран-

ства исходов опыта. Запишите такие события:

а) произошло только А,

б) произошло одно и только одно из данных событий,

в) произошли два и только два из данных событий,

г) произошли все три события,

д) произошло хотя бы одно из данных событий,

е) ни одно из событий не произошло.

РЕШЕНИЕ:

а)

А

,

B

C

б)

(A

)+(

B

)+(

C ),

B

C

A

C

A

B

в)

(A B

)+(A

C )+(

B C ),

C

B

A

г)

A B C ,

д) A + B +C ,

е)

.

A

B

C

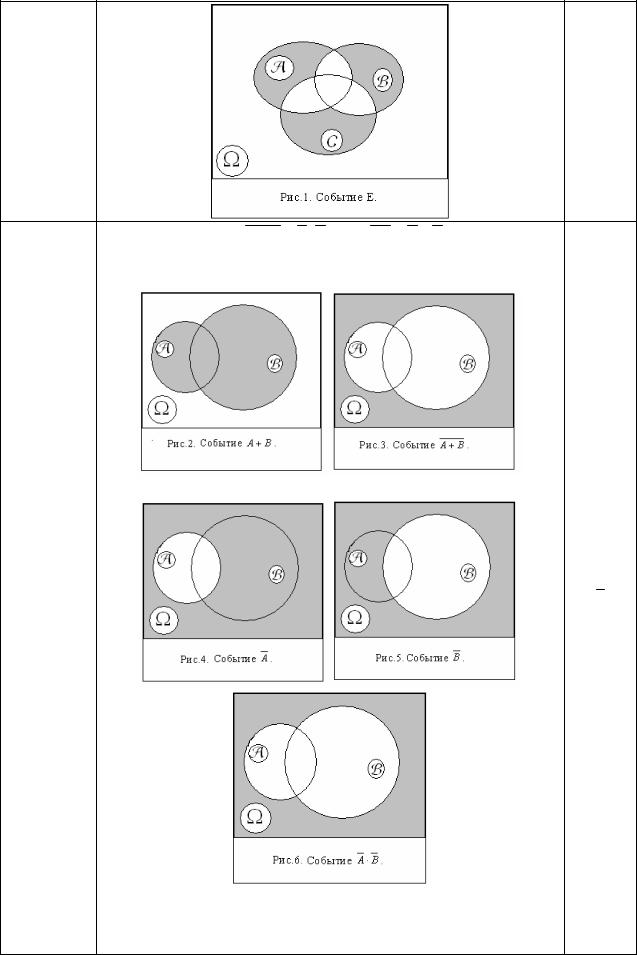
ПП 2.1.

Пусть для трех событий A, B, C выполняется событие Е

№7

{произойдет только одно из событий A, B, C}:

Постройте множество всех элементарных исходов и со-

став всех подмножеств, соответствующих событию Е.

РЕШЕНИЕ:

Ω ={

}

ABC,ABC,ABC,ABC,ABC,ABC,ABC,ABC

E ={

}

ABC,ABC,ABC

.

3

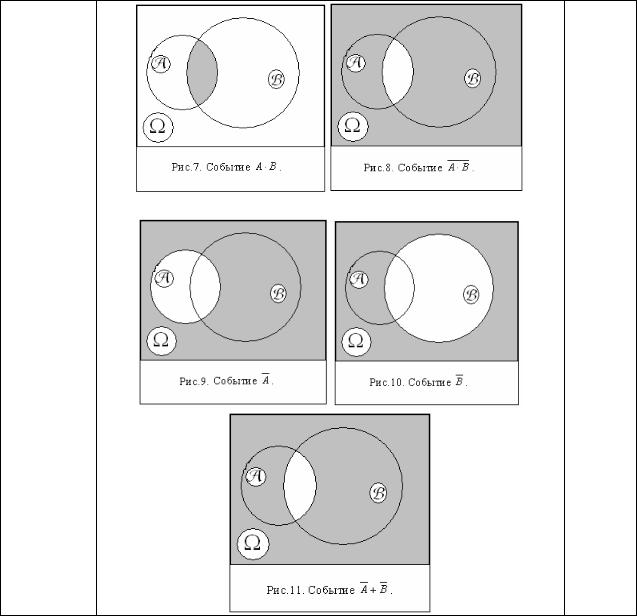
ПП 2.1.

№8

Докажите, что а) A + B = A B и б) AB = A + B . РЕШЕНИЕ:

a) Левая часть равенства:

Правая часть равенства:

4

3

б) Левая часть равенства

4

Правая часть равенства

2. Общие схемы идеализированных опытов

Рассмотрим множество или генеральную совокупность из п элементов. Многие опыты предполагают извлечение из генеральной совокупности некоторого подмножества из k элементов. Для наглядности можно представить, что элементы выбираются один за другим.

В этом случае возможны две процедуры.

Первая – выбор с возвращением, когда каждое извлечение делается из полной генеральной совокупности, так что один и тот же элемент может быть выбран несколько раз.

Вторая процедура – выбор без возвращения, когда элемент, выбранный однажды, исключается из генеральной совокупности.

В зависимости от условий опыта и искомых вероятностей мы приходим к сочетаниям, перестановкам или размещениям с повторениями или без них в качестве выборок из генеральной совокупности.

5

1.Схема выбора k элементов из п элементов без упорядочения и без возвращения приводит к сочетаниям. Число таких выборов N(Ω) = Cnk .

2.Схема выбора k элементов из п элементов без упорядочения c возвращением приводит к сочетаниям с повторениями.

Число таких выборов N(Ω) = Dnk .

3.Схема выбора k элементов из п элементов без возвращения с упорядочением приводит к размещениям.

Число таких выборов N(Ω) = Ank .

В частном случае k=n такие выборки становятся перестановками, их число N(Ω) = Рn.

4.Схема выбора элементов k из п элементов с упорядочением и с возвраще-

нием приводит к размещениям с повторениями. Число таких выборов

N(Ω) = пk.

5.Схема разбиения генеральной совокупности объема п на подмножества из

ki (i=1, 2, …, r) элементов приводит к N(Ω) = (k1, k2, … kr) числу возможных способов размещений.

3. Классическое определение вероятности

Обозначим множество исходов опыта через Ω = {ω 1, ω 2,…, ω n}, где ω i (i = 1, 2,…n) – i-ый исход из п равновозможных.

Число элементарных исходов опыта N(Ω) = n.

Пусть событию А отвечают исходы А = {ω 1, ω 2,…, ω k}, A Ω, N (A) = k. В классическом определении вероятности полагают, что для опыта с равновозможными исходами вероятности элементарных исходов равны между со-

бой и P (ω i) = P(ωj )= 1n , (i, j = 1, 2, … n).

Вероятность Р(А) события А

равна отношению числа элементарных событий, входящих в А, к общему числу элементарных событий в Ω:

Р (А) = NN((ΩA)) = kn ,

где k – число исходов опыта, благоприятствующих наступлению события А, а п – общее число событий опыта.

Для определения вероятности события мы должны уметь подсчитывать число как всех возможных исходов опыта, так и число исходов, при которых наступает интересующее нас событие с помощью комбинаторного анализа.

4. Формулы комбинаторики

Число перестановок из п элементов

Pn = n!

Число размещений из п элементов по k

6

	Ak = n (n −1) ... (n − k +1)=	n!
		(n − k )!
	n

Число сочетаний из п элементов по k

	Cnk =	n!		=	n(n -1)...(n - k +1)	=	Ak
							n
		k !(n - k)!			k !		k !

Число разбиений множества из n элементов на группы из k1, k2, …, kr элементов

Cn (k1 , k2 ,...kr )=

n!

k !k

2

!...k

r

!

1

Число сочетаний из п элементов по k с повторениями

Dk

=Cn−1

= Ck

n

n+k −1

n+k −1

ПП 2.2. Классическое определение вероятности

№ п/п

Задание

Ответ

Имеются 6 ключей. Какова вероятность выбрать

ПП 2.2.

нужный ключ?

РЕШЕНИЕ:

0,16

№1

P (A)

=

N (A)

=

1

= 0,16 .

N (Ω)

6

ПП 2.2.

В книге 500 страниц. Чему равна вероятность того,

№2

что наугад открытая страница будет иметь порядко-

вый номер, кратный 7?

РЕШЕНИЕ:

N (Ω)=5000.

Номер страницы, кратный 7, имеет вид 7k, где k ─

0,142

целое число, 0 < 7k <500 , k <

500

=

71 3

k = 71. Из них

7

7

благоприятствуют наступлению интересующего нас

события N (A)= 71.

P (A)=

N (A)

=

71

= 0,142 .

N (Ω)

500

ПП 2.2.

На 5 карточках написаны буквы А, К, Л, О, Д. Какова

№3

вероятность того, что при случайном последователь-

ном выборе карточек получится слово «ЛОДКА»?

РЕШЕНИЕ:

Число возможных расположений пяти букв на пяти

0,008

местах равно N (Ω)= P5 = 5! =120 . Так как нас инте-

ресует одна комбинация из них, то:

P ( A) =

N (A)

=

1

= 0,008 .

N (Ω)

120

ПП 2.2.

Из 5 карточек с буквами А, В, Б, Г, Д, наугад одна за

0,017

№4

другой выбираются три и располагаются в ряд в по-

7

рядке появления. Какова вероятность того, что полу-

чится слово «ДВА»?

РЕШЕНИЕ:

Число возможных расположений пяти букв на трех

местах равно N (Ω) = A53 . Так как нас интересует од-

на комбинация из них, то:

P ( A) =

N (A)

=

1

=

1

=

1

= 0,017 .

N (Ω)

A53

5 4 3

60

ПП 2.2.

Ребенок играет с четырьмя буквами разрезной азбуки

№5

А, А, М, М. Какова вероятность того, что при слу-

чайном расположении букв, в ряд получится слово

«МАМА»?

РЕШЕНИЕ:

Число способов расположить букву «М» на двух

местах из четырех равно C42 , а букву «А» на двух ос-

0,167

тавшихся – C22 .

Число возможных последовательностей этих пар

букв равно N(Ω) = C42 C22 .

Нас устраивает одна из этих комбинаций, поэтому:

P ( A) =

N(A)

=

1

=

1

=

1

=

1 =0,167.

N (Ω)

C42

C22

4!

4 3 2

6

2!2!

2 2

ПП 2.2.

Дан набор букв М, М, Т, Т, А, А, А, Е, И, К.

№6

Какова вероятность того, что при случайном раскла-

дывании получится слово «МАТЕМАТИКА»?

РЕШЕНИЕ:

М

М

Число упорядоченных комбинаций из данных букв

(М, А, Т, Е, И, К) равно числу сочетаний из п эле-

ментов с повторениями:

≈ 0,66 10−4

N(Ω) = C10

(2, 3, 2, 1, 1, 1).

Нас интересует одна из таких комбинаций, вероят-

ность ее появления равна

P (A)=

N (A)

=

1

=

2! 3! 2!

=

N (Ω)

C10

(2, 3, 2 )

10!

=

1

≈ 0,000066

151200

ПП 2.2.

Набирая номер телефона,

абонент забыл последние

№7

три цифры, и, помня лишь, что эти цифры различны,

набрал их наудачу. Найдите вероятность того, что

0,0083

набраны нужные цифры.

РЕШЕНИЕ:

8

P (A) =

N (A)

=

1

=

1

=

1

= 0,0083 .

A103

N (Ω)

10

9 8

720

ПП 2.2.

При наборе телефонного номера абонент забыл две

№8

последние цифры и набрал их наугад, помня только,

что эти цифры нечетные и разные. Найдите вероят-

ность того, что номер набран правильно.

РЕШЕНИЕ:

0,05

Число возможных расположений пяти нечетных

цифр (1, 3, 5, 7, 9) на двух местах равно A52 .

Вероятность набора единственно верной комбинации

P ( A) =

N (A)

=

1

=

1

=

1

=0,05 .

N (Ω)

5 4

A52

20

ПП 2.2.

В лотерее 2000 билетов. Из них выигрышных биле-

№9

тов: 1 ─ 100 руб., 4 ─ 50 руб., 10 ─ 20 руб., 20 ─ 10

руб., 165 ─ 5 руб., 400 ─ 1 руб., остальные ─ невыиг-

рышные. Какова вероятность выиграть по билету не

0,0175

менее 10 руб.?

РЕШЕНИЕ:

P(A)=

N (A)

=1+4 +10 + 20 =

35

= 0,0175 .

2000

N (Ω)

2000

ПП 2.2.

Числа натурального ряда 1,2,3,….n расставлены слу-

№10

чайно. Какова вероятность того, что числа 1 и 2 рас-

положатся рядом и притом в порядке возраста-

ния?

РЕШЕНИЕ:

Число способов N (Ω) расставить n чисел нату-

рального ряда равно Pn

= n!.

Число способов, когда числа 1 и 2 стоят на первом

1

и втором местах, равно числу перестановок осталь-

n

ных (n −2) чисел на остальных местах: Pn−2 = (n −2)! .

Различных положений чисел 1 2, когда они находят-

ся рядом в порядке возрастания: (n −1).

Событие А {числа 1 и 2 расположатся рядом и

притом в порядке возрастания}.

N (A)=(n −2)!(n −1)=(n −1)!.

P (A)=

N (A)

=

(n −1)!

= 1 .

n!

N (Ω)

n

ПП 2.2.

В театре, в одном ряду, содержащем 15 мест, произ-

№11

вольно рассаживаются 8 человек. Какова вероятность

0,133

того, что два определенных лица окажутся рядом?

РЕШЕНИЕ:

9

Число способов N (Ω) рассадить 8 человек по 15

местам равно N (Ω)= A158 =157!! . Число благоприятст-

вующих исходов: два соседних кресла в ряду из 15 можно расположить 14 способами (1-2, 2-3, и т.д.), эти два места соседи могут занять двумя способами; остальные 6 человек могут рассаживаться на остав-

	шихся 13 местах A6 способами, откуда
	13			= 2 14 13! = 2 14! .
	N (A)=14 2 A6
			13	7!	7!
		N (A)
	P (A)=		= 2 14! 7! =			2	= 0,133.
		N (Ω)			15
				7! 15!

ПП 2.2. Вокруг круглого стола стоят 12 стульев. 12 человек №12 занимают места за столом в случайном порядке. Какова вероятность того, что два определенных лица

окажутся рядом? РЕШЕНИЕ:

1 способ. Число способов рассадить12 человек по 12 стульям равно P12 =12!. Число благоприятствующих

исходов: два соседних стула в круге из 12 можно расположить 12 способами (1-2, 2-3,…11-12, 12-1),

эти два места соседи могут занять двумя способами; 0,(18) остальные 10 человек могут рассаживаться на ос-

тавшихся 13 местах P10 способами, откуда

P(A)= NN ((ΩA)) = 2 1212!10! =122 1211 =112 .

2 способ. Первый человек занимает 1 стул, оставшихся стульев – 11, из них соседних – 2. Вероятность второму человеку занять соседний стул –

112 = 0,(18).

ПП 2.2. В группе из 12 студентов, среди которых 8 отлични- №13 ков, по списку наудачу отобрали 9 студентов. Найдите вероятность того, что среди отобранных студентов

5 отличников. 0, 25 РЕШЕНИЕ:

	P (A)=	N (A)		C85 C44	8!			4! 9! 3! 14
			=		=				12! = 55 ≈ 0, 25.
		N (Ω)		C129		5! 3!		4! 1!
ПП 2.2.	Сколько существует способов раздать 10 вариантов									1814400;
№14	контрольной работы восьми студентам? Какова ве-									0,0(2)
	роятность события A{варианты 1 и 2 окажутся неис-

10