Конспект лекций-2010

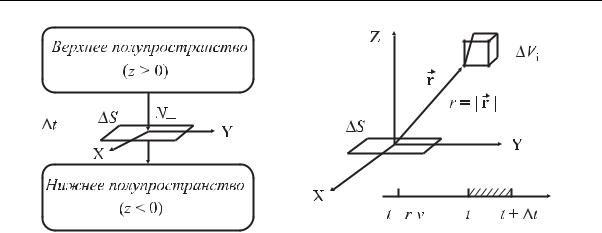
2.2. Плотность диффузионного тока нейтронов

Рис. 2.2. Пояснение к расчету плотности тока нейтронов
результирующий ток N− как сумму
N−( S, t) = ∑ Ni( S, t),			(2.2)
i

где Ni – вклад элементарного объема Vi в результирующий ток N− через площадку S. Однако не все частицы, находящиеся в объеме Vi, дадут вклад в Ni. Вероятность такого “удачного” события p определяется тремя независимыми событиями:

a) в результате столкновения произойдет рассеяние, а не поглощение нейтрона (пусть вероятность этого события равна p1);

б) направление движения рассеявшегося нейтрона будет ориентировано на площадку S (вероятность этого события обозначим p2); в) ориентированный нейтрон не будет выведен из “пучка” при дви-

жении к площадке (вероятность этого события обозначим p3).

Очевидно, вероятность реализации “удачного” столкновения равна произведению вероятностей трех независимых событий:

p = p1 ·p2 ·p3.

(2.3)

При заданном поле n(r,t) количество частиц в элементарном объеме Vi любой момент времени t будет

F Vi,t n(r,t )· Vi.

(2.4)

Для того чтобы нейтрон “попал” во временное´ “окно” регистрации от t до t + t, он должен претерпеть рассеяние заранее, в промежутке времени от t до t + t , причем t = t −τ. Здесь опережение τ = r/v – время, необходимое нейтрону, движущемуся со скоростью v, для прохождения расстояния r от объема Vi до площадки S (взаимодействие

29

Глава 2. Односкоростное диффузионное уравнение

предполагается мгновенным). Тогда можно определить вероятность p из отношения

p =	Ni(	S, t)	.	(2.5)
	F (
		Vi,t )

Если количество частиц, рассеянных в объемеVi за время от t до t + t обозначить через Ci ( Vi, t), то по определению

p1	=	Ci ( Vi, t)	.	(2.6)
		F ( Vi,t )

Подставляя эти соотношения в (2.3) и сократив знаменатели в левой и правой частях, получим

	Ni( S, t) =Ci ( Vi, t)·p2 ·p3.	(2.7)
Количество рассеяний в объеме Vi за промежуток времени		t полу-
чается интегрированием плотности рассеяний:
Ci =	dt Σs ·ϕ(r,t −r/v)dV ≈ Σs ·ϕ(r,t −r/v)· Vi · t.	(2.8)
t	Vi

Здесь, в силу малости промежутков Vi и t, дважды применена теорема о среднем.

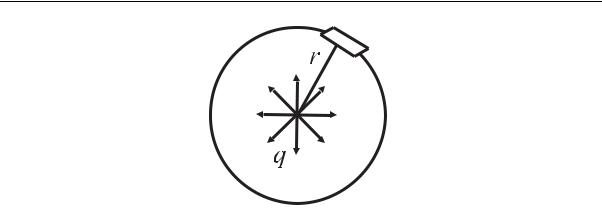
Рассеяние, по условию 3, изотропно. Это означает, что в единичный телесный угол вылетает после рассеяния одинаковое количество нейтронов, а именно 1/4π нейтронов. Рассмотрим точечный изотропный источник мощностью q нейтрон/с, окруженный сферой радиуса r (рис. 2.3). Пусть источник расположен в вакууме, т.е. взаимодействие со средой отсутствует. Вычислим количество нейтронов, пересекающих в 1 с площадку размером 1 см2 на поверхности сферы. Пусть эта величина равна j. Если ее умножить на площадь поверхности сферы 4πr2, найдем число нейтронов, пересекающих в 1 с поверхность всей сферы. Нейтроны не взаимодействуют внутри сферы, поэтому мощность источника равна мощности выхода нейтронов с поверхности

	сферы:			q
	j ·4πr2 = q,	отсюда	j =			(2.9)
					.
				4πr2

Вернувшись к задаче ориентации нейтрона в сторону площадки S, найдем вероятность для нейтрона вылететь в направлении площадки:

S ·cos θ

p2 = 4πr2 . (2.10)

30

2.2. Плотность диффузионного тока нейтронов

Рис. 2.3. Точечный изотропный источник в вакууме, окруженный сферой r

Множитель 1/4π объяснен выше (см. (2.9)). Множитель S ·cos θ представляет собой “видимый размер” площадки S из точки r, который,

очевидно, зависит не только от величины площадки	S, но и от ее
ориентации относительно точки r.
Осталось “довести” нейтроны (2.10) до площадки	S. На пути от

точки r до площадки нейтроны будут претерпевать и рассеяния, и поглощения. Некоторые рассеяния незначительно отклонят нейтроны от первоначального направления, и они пересекут площадку S. Надо ли их учитывать? Да, и они будут учтены посредством интегрирования по объему, когда будут суммироваться вклады всех рассеивающих точек. Поэтому следует считать, что каждое столкновение выводит нейтроны из пучка (2.10). Вспомнив закон ослабления пучка (1.30),

запишем

j(r)

p3 =

= exp (−Σ ·r).

(2.11)

J0

Собирая все вместе и подставляя в (2.7), получим

Ni( S, t) =

S ·cos θ

·

Σs

·

ϕ(r,t

−

r/v)

·

exp[

−

(Σa +Σs)

·

r] Vi t. (2.12)

4πr2

Остается просуммировать вклад объема

Vi

(2.12) по всем объемам

Vi верхнего полупространства. Уменьшая объемы разбиения полу-

пространства: maxi			( Vi) → 0, переходим к интегралу:
N dV ≡	Σs	S		t cos θ				·exp [−(Σs +Σa)·r]·ϕ(r,t −r/v)dV.	(2.13)
		4π				r2
V				V
z>0				z>0

Как следует из выражения (2.13), количество нейтронов, пересекающих площадку за промежуток времени t, – величина аддитивная. Ее

31

Глава 2. Односкоростное диффузионное уравнение

производная j_ называется плотностью тока нейтронов, пересекающих единичную площадку в плоскости (х,у) за единичный промежуИнтеграл (2.13) запишем в сфериче-

ток времени в направлении (−z).	2	dr ·sin θdθdψ:
ской системе координат, где V = r

	≡ t→→0		1	V
j_	lim		S t		CSGP dV		=
	S 0

×exp [−(Σs +Σa)·

Σ ∞	2π		π/2
4πs 0	dr 0	dψ 0 ϕ(r,t −r/v)×
r]cos θsin θ dθ.				(2.14)

Подынтегральное выражение в (2.14) содержит быстро убывающую функцию exp(−.): при расстояниях r > 3 ·l, где l = 1/(Σs +Σa) – длина свободного пробега, экспонента убывает более чем в 20 раз. Из этого следует, что основной вклад в интеграл дают рассеяния вблизи площадки. Разложим функцию ϕ в ряд Тейлора вблизи начала координат и сформулируем еще одно ограничение диффузионной теории. Предположим,

что на расстояниях до трех длин свободного пробега функция плотности потока нейтронов ϕ(r,t) хорошо описывается членами нулевого и первого порядка разложения в ряд Тейлора.

По условию 5 на данных расстояниях плотность потока меняется незначительно и можно приближенно считать ϕ(r,t −r/v)≈ϕ(r,t). Запишем цепочку упрощений:

ϕ(r,t −r/v)≈ ϕ(r,t) ≈ ϕ0 +x ·	∂ϕ	0	+y ·	∂ϕ	0	+z ·	∂ϕ	0 .	(2.15)
	∂x			∂y			∂z

Здесь индекс “0” означает, что соответствующая величина берется в начале координат. Наконец, вспомним ограничение 4 и заменим в показателе экспоненты: Σs +Σa ≈ Σs.

Для вычисления интеграла (2.14) подставим разложение (2.15) в выражение (2.14) и рассмотрим каждый член получившейся суммы:

Σ

0 0

π/2

∂ϕ

∂ϕ

∂ϕ

0

∞

2π

ϕ0 +x

·e−Σs·r cos θ ·sin θdθ =

s

dr

dψ

0+y

0+z

4π

∂x

∂y

∂z

0

= A

+B +C +D.

(2.16)

32

2.2.Плотность диффузионного тока нейтронов

1.Вычисления начнем с интеграла A:

Σs

∞

2π

π/2

Σsϕ0

∞

0

dr

dψ ϕ0 ·e−Σs·r cos θ ·sin θdθ =

2π

e−Σs·r dr

cos θd(cos θ) =

4π

4π

0

0

0

0

π/2

0

0

∞

cos2 θ

ϕ

ϕ

ϕ

∞

1

Σs2

0

= −

2

π/2

·

0

Σs d(e−Σsr) = −

= 40 .

(2.17)

40 e−Σsr

2.Обратимся к вычислению интеграла B, вспомнив связь (1.15)

x= r ·sin θ ·cos ψ:

Σ

∞

2π

π/2

∂ϕ

0

x ·

s

dr0

dψ

·e−Σs·r cos θ ·sin θdθ =

4π

0

0

∂x

∂ϕ

0

Σ

∞

π/2

2π

= ∂x

·

4πs

0

r ·e−Σs·r dr

0

cos θ ·sin2 θdθ

0

cos ψdψ =

2π

∞

π/2

∂ϕ

Σ

0

0

= sin ψ

·

∂x 0· 4πs

r ·e−Σs·r dr cos θ ·sin2 θdθ = 0.

(2.18)

0

=0

3.Интеграл C равен нулю, поскольку он представляет собой интеграл от периодической по ψ функции на интервале периода 2π.

4.Остается вычислить интеграл D, заменив z = r ·cos θ:

Σ

∞

2π

π/2

∂ϕ

s

dr0

dψ

z ·

0 ·e−Σs·r cos θ ·sin θdθ =

4π

0

0

∂z

Σ

∂ϕ

∞

π/2

0 2π0

=

4πs

∂z

r ·e−Σs·r dr

0

cos2 θ ·sin θdθ =

=

∂ϕ

0

Σ

∞

0

∂z

·

2s ·0

r ·e−Σs·r dr

cos2 θd(cos θ) =

π/2

33

Глава 2. Односкоростное диффузионное уравнение

0

cos3 θ 0

∂ϕ

Σ

∞

=

·

0 ·

s

· r ·e−Σs·r dr =

3

π/2

∂z

2

∞

∞

Σ

0

r

1 ∂ϕ

∂ϕ

= −

s

·

0 ·

d(e−Σs·r) = −

·

0 ·r ·e−Σs·r0

+

6

∂z

Σs

6

∂z

1

=0

1

∂ϕ

∞

1

∂ϕ

∞

1

∂ϕ

+

0

·0

e−Σs·r dr

=

0

·0

d(e−Σs·r) =

0

. (2.19)

6

∂z

6

∂z

Σs

6Σs

∂z

При вычислениях применена формула интегрирования по частям. Запишем окончательное выражение для диффузионной плотности тока, направленного против оси z:

	ϕ		1	·	∂ϕ	0 .
j_ =	0	+					(2.20)
	4		6Σs		∂z

Отличия вычислений плотности тока в положительном направлении оси z состоят в изменении пределов интегрирования по углу θ: в этом

случае интегрируется от π/2	до π и диффузионная плотность тока j+
отличается только знаком:				·		0 .
	ϕ		1		∂ϕ
j+ =	40	−			∂z		(2.21)
			6Σs

Результирующая плотность тока в положительном направлении оси z равна разности между j+ и j_:

j+z = j+ − j_ = −	1	·	∂ϕ	0	= −D ·	∂ϕ	0	,	(2.22)
			∂z			∂z
	3Σs

где D = (3Σs)−1 – обычное обозначение коэффициента диффузии. При получении формул для плотности тока были введены ограни-

чения, которые могут быть в значительной степени сняты. Это будет сделано ниже, после вывода диффузионного уравнения.

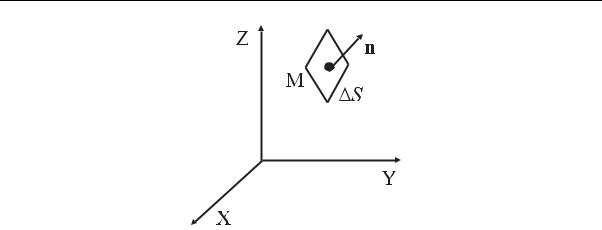
Обобщим полученный результат. Если площадка S ориентирова-

на произвольно (рис. 2.4), то можно убедиться, что плотности тока нейтронов в направлении нормали и в противоположном направлении таковы:

j+ =

ϕM

−

1

·

∂ϕ

M

,

4

6Σs

∂n

(2.23)

_

∂n M

4

− 6Σs

·

ϕM

1

∂ϕ

=

.

j

34

2.2. Плотность диффузионного тока нейтронов

Рис. 2.4. Произвольная ориентация элементарной площадки S

Здесь ∂ϕ/∂n – производная по нормали: индекс M означает, что соответствующая величина берется в точке M S. Результирующая плотность тока в точке M в направлении n

jn = j+ − j_ = −	1	·	∂ϕ	M	= −D ·	∂ϕ	M .	(2.24)
	3Σs		∂n			∂n

Из формулы (2.24) следует, в частности, что результирующее перетеканиенейтроновпроисходитизобластисбольшейплотностьювобласть с меньшей плотностью: если jn >0, то с необходимостью ∂ϕ/∂n <0, т.е. ток положителен в сторону убывания функции ϕ, а значит, и функции плотности нейтронов n(.) (ϕ ≡ n(.)·v)

Воспользовавшись известной формулой ∂ϕ/∂n = n · ϕ, перепишем выражение (2.24) в виде

jn = −D ·	∂ϕ	M	= −D ·n · ϕ.	(2.25)
	∂n

Величина (−D ·n · ϕ) называется векторным током нейтронов j:

j = −D ·n · ϕ ≡ −D ·gradϕ,

(2.26)

и результирующая плотность тока (2.25) может быть записана как скалярное произведение:

jn = (j ·n).

(2.27)

Отметим,чтовсевыражениядляплотностидиффузионноготока(2.22)– (2.27) с точки зрения математики представляют собой первый закон Фика (Адольф Фик, 1855).

35

Глава 2. Односкоростное диффузионное уравнение

2.3. Вывод диффузионного уравнения

Обратимся к рис. 2.1 и получим компоненты балансного соотношения для конечного объема V за малый промежуток времени t. При заданном поле n(r,t) количества нейтронов в объеме V в момент времени t и в момент времени t + t соответственно равны

Nv(t) = n(r,t)dV ;	Nv(t + t) = n(r,t + t)dV.	(2.28)
V	V

Следовательно, приращение количества нейтронов в объеме V за промежуток времени t:

Nv( t) = [n(r,t + t)−n(r,t)] dV.	(2.29)
V

Изменение количества нейтронов (2.29) обусловлено: а) источниками; б) поглощением и в) диффузионным перетеканием через поверхности объема V . Вычислим последовательно эти компоненты уравнения баланса:

а) если плотность распределения источников q(r,t), то соответствующий вклад источников Nq за промежуток времени t

Nq = t · q(r,t)dV ;	(2.30)
V
б) количество поглощений в объеме V за промежуток времени	t Na

вычисляется интегрированием плотности поглощающих столкновений:

Na = t · Σa ·ϕ(r,t)dV ;	(2.31)
V

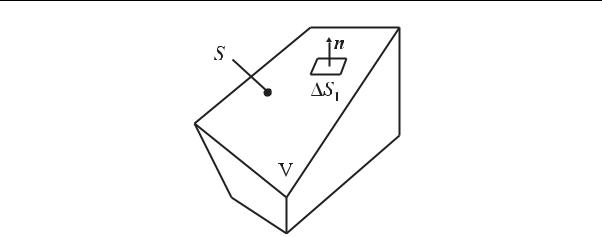
в) для вычисления перетекания нейтронов через поверхность S объема V (рис. 2.5) разобьем поверхность S на элементарные площадки Si. Через каждую площадку Si за промежуток времени t в направлении нормали выходит, в соответствии с выражением (2.25), t ·(−D ·n · ϕ)· Si нейтронов. Для определения количества нейтронов Nsur, выходящих через всю поверхность объема V за время t, необходимо просуммировать вклады всех площадок. Устремив, далее, максимум разбиения Si к нулю, приходим к интегралу по замкнутой поверхности S, ограничивающей объем V:

Nsur = t · (−D ·n · ϕ(r,t)) dS.	(2.32)
S

36

2.3. Вывод диффузионного уравнения

Рис. 2.5. Элементарная ориентированная площадка Si на поверхности S объема V

Воспользуемся теоремой Остроградского-Гаусса и переведем поверхностный интеграл в объемный, так как величины всех остальных вкладов Nv,q,a – объемные интегралы:

Nsur = t (−D ·n · ϕ(r,t)) dS = t	(−D ·n · ϕ(r,t)) dV. (2.33)
S	V

Запишем, наконец, соотношение баланса (см. рис. 2.1):

	Nv =		Nq − Na − Nsur → [n(r,t +		t)−n(r,t)] dV =
				V
	=			t · [q(r,t)−Σa ·ϕ(r,t)+ D ϕ(r,t)] dV.		(2.34)
				V	t → 0, получим
Поделим обе части (2.34) на t и, устремив
		r,t	)	−q(r,t)+Σa ·ϕ(r,t)− D ϕ(r,t) dV = 0.
		∂n(				(2.35)
V		∂t

Ввидупроизвольностиобъемаинтегрированияинепрерывностиподынтегральной функции из (2.35) следует

∂n	− D ϕ +Σa ·ϕ −q = 0.	(2.36)
∂t

Перейдем к одной функции ϕ ≡ n ·v и получим диффузионное уравне-

ние			∂ϕ
1		·		= D ϕ −Σa ·ϕ +q.	(2.37)
	v		∂t

37

Глава 2. Односкоростное диффузионное уравнение

В однородной среде коэффициент диффузии D не зависит от координат: D = const, поэтому уравнение упрощается:

1	·	∂ϕ	= D ·Δϕ −Σa ·ϕ +q,	(2.38)
		∂t
v

где ≡ 2 – оператор Лапласа, о котором см. п.2.1. Очень часто в приложениях возникают стационарные задачи (например, при работе реактора на постоянной мощности), в которых плотность потока не изменяется во времени, т.е. ∂ϕ/∂t = 0. В этом случае рассматривают стационарное диффузионное уравнение

D ·Δϕ −Σa ·ϕ +q = 0.

(2.39)

Отметим, что уравнение диффузии с точки зрения математики представляет собой второй закон Фика (Адольф Фик, 1855).

2.4. Ограничения диффузионного приближения

Обратимся теперь к ограничениям,сделанным перед выводом формулы для диффузионного тока, и рассмотрим, могут ли они быть сняты или ослаблены. Кратко повторим здесь эти ограничения.

1. Среда бесконечна и однородна.		Ограничение 1 может быть снято в
2.	В среде нет источников.	том смысле, что среда может быть
3.	Рассеяние изотропно в L.	и конечной, но оптические разме-
4.	Σa Σs, Σs ≈ Σ.	ры ее в длинах свободного пробега
		должны быть достаточно велики.
5.	τ = 1/v ≤ T .	Более того, удовлетворительными

следует считать те результаты, полученные по диффузионной теории, которые относятся к областям, удаленным от границ не менее чем на 2-3 длины свободного пробега.

Ограничение2 также может быть ослаблено, если плотность источников в среде относительно плотности рассеивающих столкновений мала, т.е. q(r) ϕ ·Σs, что на практике обычно наблюдается. В практических задачах обычно соблюдается и ограничение 5.

Окончательно сформулировать условия применимости диффузионного приближения можно следующим образом:

38