матлог

Свойства операций над множествами.			3.	Существование универсальных границ:
1.	Ассоциативность:	,		А U 0 = A: A ∩ 0 = 0: A ∩ U = U: A ∩ U = A
2.	Дистрибутивность: (AUB)∩C=(A∩C)U(B∩C),		4.	Двойное дополнение (двойное отрицание):
	(A∩B)UC=(AUC)∩(BUC)
			5.	,
	Поглощение: A U A = A, A ∩ A = A.
			6.	Законы двойственности или закон Де – Моргана
				,

Вопрос 6. Декардово произведение множеств.

Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств.

Пусть	и - множества. Выражение вида		, где	и	, называется упорядоченной парой. Равенство
вида	означает, что	и	. В общем случае, можно рассматривать упорядоченную n-ку
	из элементов		. Упорядоченные n-ки иначе называют наборы или кортежи.
Определение 4. Декартовым (прямым) произведением множеств					называется множество
упорядоченных n-ок (наборов, кортежей) вида

Определение 5. Степенью декартового произведения 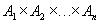называется число множеств n, входящих в это декартово произведение.

Замечание. Если все множества 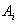одинаковы, то используют обозначение

.

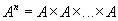Вопрос 7. 1.Фун-ии алгебры логики. 2.Представление произвольной фун-ии алгебры алгебры логики в виде формулы алгебры логики.

1. Функции алгебры логики (ФАЛ)

Радиоэлектроника в настоящее время во многом определяет научнотехнический прогресс и объединяет ряд отдельных областей науки и техники, развившихся из радиотехники и электроники.

Радиотехника - область науки и техники, связанная с разработкой устройств и систем, обеспечивающих генерирование, усиление, преобразование, хранение, а также излучение и прием электромагнитных колебаний радиочастотного диапазона, используемых для передачи информации.

Всовременных радиотехнических системах и комплексах до 90% разрабатываемых устройств реализуется на элементах цифровой и вычислительной техники и используются цифровые методы обработки сигналов.

Внастоящее время бурно развивается по экспоненциальному закону вычислительная техника и ее элементная база. А не так давно первые интегральные микросхемы (1958 год) содержали до десяти транзисторов. Сегодня современные микропроцессоры содержат до 10 миллионов транзисторов на один кристалл, и менее чем через десять лет это число достигнет 100 миллионов транзисторов.

Уже отошла в историю дискретная схемотехника, когда различные узлы строились на печатных платах с использованием отдельных навесных радиоэлектронных компонентов: транзисторов, резисторов, конденсаторов и

11

других элементов. Ранее соединения выполнялись с помощью внешнего печатного монтажа, теперь соединения и монтаж осуществляется внутри кристалла. Поэтому современный инженер электронной техники должен владеть передовыми методами и технологиями, чтобы уметь приспособить их завтра к вычислительной технике будущих поколений, овладеть практическими приемами проектирования устройств на программируемых логических интегральных схемах.

Логические выражения n двоичных переменных с помощью конечного числа логических операций можно рассматривать как некоторую функцию, отражающую взаимную связь между входными и выходными переменными.

Логические операции конъюнкции 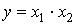и дизъюнкции 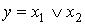можно представить простейшими

функциями вида: 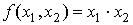и 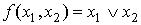. Эти функции называются аналогично логическим операциям – функциями И и ИЛИ.

Такие ФАЛ подобно логическим выражениям могут быть заданы аналитическим и табличным способами. При аналитическом способе ФАЛ задается в виде логических выражений, получаемых путем логических преобразований с помощью законов и правил Булевой алгебры.

При табличном способе ФАЛ задается таблицей истинности, где число всех возможных наборов (комбинаций)

аргументов конечно. Если число аргументов ФАЛ равно n, то число их возможных наборов 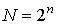, а число

различных функций 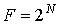, тогда при n=2, F=16. Составим таблицу истинности для функций двух аргументов. Таблица 1.

Аргументы		Функции
			.
0	0	0	0	0	0		0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0		1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1		0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1		0	1	0	1	0	1	0	1	0	1	0	1
В таблице 1 приведены элементарные ФАЛ									двух аргументов. В левой части таблицы перечислены все

возможные наборы аргументов и 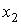, в правой части приведены значения ФАЛ на соответствующих входных наборах. Значения всей совокупности этих наборов переменных представлены в таблице последовательностью чисел в двоичной системе счисления.

Каждая ФАЛ 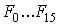обозначает одну из 16 возможных логических операций над двумя переменным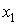и и 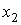, имеет свою таблицу истинности, собственное название и условное обозначение.

Основные сведения об элементарных функциях 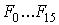даны в таблице 2. Таблицы истинности для каждой ФАЛ составляются отдельно по таблице 1.

Таблица 2

		Операционные	Обозначения, названия	Зарубежные аналоги
	Функция	символы
		0	Константа 0	Const 0
			И – лог. умножитель	AND –
				Conjunctor
			Запрет	Inhibition
			Повторитель	BF – Buffer
			Запрет	Inhibition
				BF – Buffer
			Повторитель
			Исключающее ИЛИ	Exlusive – OR

12

		ИЛИ – лог. сумматор	OR – Disjunctor
		ИЛИ – НЕ, функция	NOR,
		Пирса	Peers F.
		Исключ. ИЛИ – НЕ	EX – NOR
			NOT – Invertor
		НЕ – инвертор
		Импликатор	Implicator
			NOT – Invertor
		НЕ – инвертор
		Импликатор	Implicator
		И – НЕ, функция	NAND, Shaffer
		Шеффера	F.
	1
		Генератор 1	Generator 1
В таблице 2 часто применяемыми являются функции:
	-повторители 1-го и 2-го аргументов;
	– инверсии 1-го и 2-го аргументов;
– функция И (конъюнкция), логическое умножение;

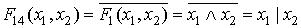– функция И-НЕ (базис Шеффера);

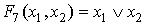– функция ИЛИ (дизъюнкция), логическое сложение;

– функция ИЛИ-НЕ (базис Пирса);

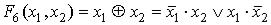– функция неравнозначности, реализуется ЛЭ ―Исключающее ИЛИ‖ (сумматор по модулю два);

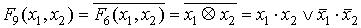– функция равнозначности реализуется ЛЭ ―Исключающее ИЛИ-НЕ‖.

Рассмотренные элементарные функции двух аргументов играют важную роль при преобразованиях сложных логических выражений, а также при преобразовании функциональных цифровых узлов.

Функции n переменных, значения которых заданы во всех точках области определения, считаются полностью определенными ФАЛ. Если какая-либо функция имеет запрещенные наборы переменных и ее значения на указанных наборах не определены, то такая ФАЛ называется не полностью определенной. Такие наборы будем отмечать в таблицах истинности (*) и при необходимости доопределять их значениями 0 и 1. Эти вопросы будут рассматриваться позже.

Логические функции, которые считаются полностью определенными, могут быть представлены различными формами. ДНФ – дизъюнктивная нормальная форма записи ФАЛ представляется в виде суммы (дизъюнкции) ряда элементарных

13

членов (минтермов), каждый из которых является произведением (конъюнкцией) аргументов или их инверсий. Термин ―нормальная форма‖ предполагает, что в логическом выражении, задающем функцию, последовательно выполняются не более двух базовых операций (кроме инверсии).

Запишем ФАЛ в ДНФ:

;

(1)

Функцию (3.19) можно записать в виде дизъюнкции минтермов:

,

где - конъюнкции аргументов ФАЛ, называемые минтермами.

СДНФ – совершенная дизъюнктивная нормальная форма записи ФАЛ представляется в ДНФ, где в каждом элементарном члене (минтерме), имеющем одинаковую размерность, представлены все аргументы функции или их инверсии.

Запишем ФАЛ в СДНФ:

. (2)

Если записать ФАЛ в виде:

,

(3)

то форма представления данной функции не является СДНФ, так как второй минтерм не содержит аргумент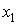а , а

также не является ДНФ, так как третий минтерм 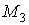не является элементарным.

Функцию 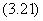можно упростить (минимизировать) и представить минимальной ДНФ (МДНФ).

(4)

Полученные элементарные члены МДНФ называются импликантами.

КНФ – конъюнктивная нормальная форма записи ФАЛ, представляется в виде произведения (конъюнкции) ряда элементарных членов (макстермов), которые являются суммой (дизъюнкцией) аргументов ФАЛ.

Запишем функцию в КНФ:

.

(5)

СКНФ – совершенная конъюнктивная нормальная форма записи ФАЛ представляется в КНФ, где в каждом элементарном члене (макстерме) представлены все аргументы функции либо их инверсии.

Запишем функцию	в СКНФ:
	.	(6)

По функциям, представленным в СДНФ и СКНФ, можно построить таблицу истинности и наоборот – по таблице истинности можно записать ФАЛ в СДНФ и СКНФ.

На основании общей табл. 1 составим таблицу истинности функции неравнозначности 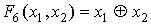и запишем ее в СДНФ и СКНФ.

На наборах N(2,3), где функция принимает значения 1, записываем ФАЛ в СДНФ, а на наборах N(1,4) – в СКНФ. При

записи ФАЛ в СДНФ аргументы x=0 записываются с инверсией 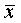, а в СКНФ – без инверсии.

При записи функции в СДНФ по таблице истинности необходимо записать столько дизъюнктивных членов (минтермов), представляющих собой конъюнкции всех аргументов, сколько единиц содержит функция в таблице. Минтермы соединяются знаком логического суммирования.

Если в наборе значение аргумента равно нулю, то в конъюнкцию входит инверсия данного аргумента.

При записи ФАЛ в СКНФ необходимо записать столько конъюнктивных членов (макстермов), сколько нулей содержит функция. Макстермы (конъюнкции аргументов) соединяются знаком логического умножения. Если в наборе значение аргумента равно нулю, то в дизъюнкцию входит аргумент без инверсии.

2. ????????????? нет ответа.

14

Вопрос 8. Закон двойственности.

Формулы А и А* называются двойственными, если формула А* получается из формулы А путем замены в ней каждой операции на двойственную.

Имеет место следующий закон двойственности: если формулы А и В равносильны, то равносильны и им двойственные формулы, т.е. А* В*.

Вопрос 9. 1.Дизъюнктивная нормальная форма и 2.совершенная дизъюнктивная нормальная форма.

1. Определение 3: Переменная 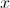или 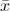называется литералом (или буквой).

Определение 4: Конъюкция литералов, встречающихся не более чем по одному разу, называется элементарной конъюнкцией. Число букв входящих в неѐ называется еѐ рангом. Элементарная конъюнкция называется полной относительно рассматриваемой булевой функции, если еѐ ранг равен числу переменных данной функции.

Определение 5: Дизъюнкция конечного множества элементарных конъюнкций называется дизъюнктивной нормальной формой(ДНФ). Число элементарных конъюнкций, образующих дизъюнктивную нормальную форму(ДНФ) называется длиной ДНФ. ДНФ содержащая только полные элементарные конъюнкции называется совершенной ДНФ(или СДНФ). Любую логическую формулу А можно представить в виде ДНФ, а затем ДНФ в виде СДНФ.

2. СДНФ (Совершенная Дизъюнктивная Нормальная Форма) — это такая ДНФ, которая удовлетворяет трѐм условиям:

в ней нет одинаковых элементарных конъюнкций

в каждой конъюнкции нет одинаковых пропозициональных букв

каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке.

Для любой функции алгебры логики существует своя СДНФ, причем единственная.

Вопрос 10. 1.Конъюктивная нормальная форма и 2. совершенная конъюктивная нормальная форма.

1. Определение 6: Дизъюнкция литералов, встречающихся не более чем по одному разу, называется элементарной дизъюнкцией. Число литералов является рангом дизъюнкции. Элементарная дизъюнкция содержащая максимальное число литералов называется полной.

Определение 7: Конъюнкция конечного множества элементарных дизъюнкций называется конъюнктивной нормальной формой(или сокращенно КНФ). Число элементарных дизъюнкций образующих КНФ называется длинной. КНФ состоящая только из полных элементарных дизъюнкций называется СКНФ. Произвольную формулу B vможно представить в виде КНФ, а затем КНФ в виде СКНФ.

2. Этот способ очень похож на предыдущий, только операции & и 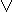меняются ролями. В скобках оказываются цепочки, соединенные операциями 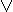, а сами скобки объединяются операциями &. Доказательство СКНФ очень похоже на доказательство СДНФ. В целом метод построения СКНФ заключается в следующем (жирным шрифтом выделены отличия от СДНФ):

Для каждой строки с нулем в крайнем правом столбце образуем скобки и объединяем их операцией &. В каждую скобку вставляем последовательность из простых элементов, объединенных операцией V: для ячейки таблицы, где проставлен 0, пишем переменную-аргумент, а для каждой ячейки, где проставлена 1, пишем переменную-аргумент со знаком ~ перед ним.

Вопрос 11. Проблема разрешимости.

15

Проблема разрешимости — вопрос, сформулированный в рамках какой-либо формальной системы, требующий ответа «да» или «нет», возможно, зависящего от значений некоторых входных параметров.

Например, проблема «дано два числа x и y, делится ли x на у?» является проблемой разрешимости. Ответ может быть дан либо «да» либо «нет» и зависит от значений x и y. Метод решения проблемы разрешимости, представленный в форме алгоритма, называется разрешающей процедурой для этой проблемы. Так, разрешающая процедура для проблемы разрешимости «дано два числа x и y, делится ли нацело x на у?» должна определять совокупность действий, которые следует предпринять для проверки делимости нацело x на у для данных x и y. Один из таких алгоритмов деление столбиком изучается в начальной школе. Остаток равный нулю означает ответ «да», иначе «нет». Проблема разрешимости, для которой существует разрешающая процедура, называется разрешимой.

Исследования в области теории рекурсии часто сфокусированы на проблемах разрешимости, поскольку к ним без потери общности сводятся многие задачи.

Вопрос 12. Релейно-контактные схемы

Релейно-контактные схемы (их часто называют переключательными схемами) широко используются в технике автоматического управления.

Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящее из следующих элементов:

1)переключателей, которыми могут быть механические устройства, электромагнитные реле, полупроводники и т.д.;

2)соединяющие их проводники;

3)входы в схему и выходы из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.

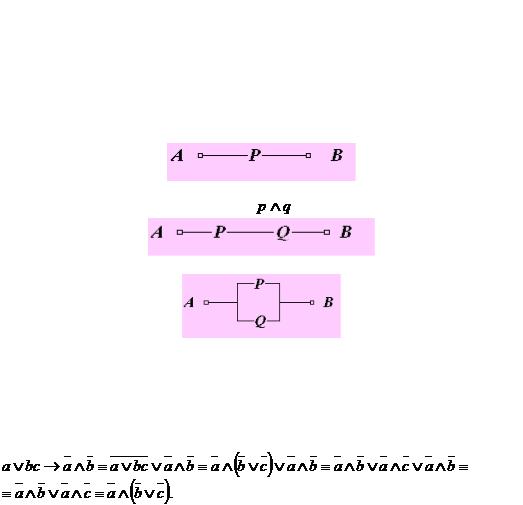
Простейшая схема содержит один переключатель Р и имеет один вход А и один выход В. Переключателю Р поставим в соответствии высказывание р, гласящее: - ―Переключатель Р замкнут ‖. Если р истинно, то импульс, поступающий на полюс А, может быть снят на полюсе В без потери напряжения, то есть схема пропускает ток. Если р ложно, то переключатель разомкнут и схема тока не проводит. Таким образом, если принять во внимание не смысл высказывания, а только его значение, то можно считать, что любому высказыванию может быть поставлена в соответсвие переключательная схема с двумя полюсами (двухполюсная схема).

Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.

Так, конъюнкции двух высказываний

ставится в соответствие схема:

а дизъюнкции 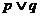- схема:

Так как любая формула может быть записана в ДНФ или КНФ, то ясно, что каждой формуле алгебры логики можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры логики.

Пример 1. По данной формуле составить РКС .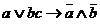

Решение. Упростим данную формулу с помощью равносильных преобразований:

16

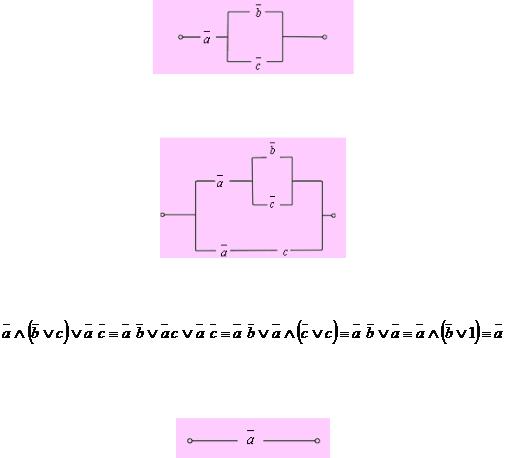
Тогда РКС для данной формулы имеет вид:

Пример 2. Упростить РКС:

Решение. Составим по данной РКС формулу (функцию проводимости) и упростим ее:

(к последним двум слагаемым применили закон поглощения).

Тогда упрощенная схема выглядит так:

Вопрос 13. 1.Исчисление высказываний. 2. Система аксиом исчисления высказываний.

1. Логика высказываний (или пропозициональная логика от англ. propositional logic, или исчисление высказываний[1]) — это формальная теория, основным объектом которой служит понятие логического высказывания. С точки зрения выразительности, еѐ можно охарактеризовать как классическую логику нулевого порядка.

Несмотря на свою важность и широкую сферу применения, логика высказываний является простейшей логикой и имеет очень ограниченные средства для исследования суждений[1].

Базовыми понятиями логики высказываний являются пропозициональная переменная — переменная, значением которой может быть логическое высказывание, и (пропозициональная) формула, определяемой индуктивно следующим образом[2]:

1.Если P — пропозициональная переменная, то P — формула.

2.Если A — формула, то — формула.

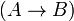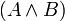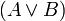3.Если A и B — формулы, то , и — формулы.

4.Других формул нет.

Множество пропозиционных формул называется языком логики высказываний (англ. propositional language, PL)[2].

Знак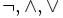и и (отрицание, конъюнкция, дизъюнкция и импликация) называются пропозициональными связками. Подформулой называется часть формулы, сама являющаяся формулой. Собственной подформулой называется подформула, не совпадающая со всей формулой.

2. Систему аксиом исчисления L составляет бесконечное счетное множество формул исчисления, построенных с использованием следующих трех схем аксиом:

17

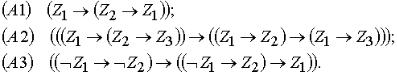
Аксиомой считается каждая формула, полученная подстановкой в схему аксиом любых формул исчисления L вместо переменных Z1, Z2, Z3.

Вопрос 14. 1.Понятие формулы исчисления высказываний. 2.Определение доказуемой формулы.

1. Исчисление высказываний – это аксиоматическая логическая система, интерпретацией которой является алгебра высказываний.

Описание всякого исчисления включает в себя описание символов этого исчисления (алфавита), формул, являющихся конечными конфигурациями символов, и определение выводимых формул.

^ Алфавит исчисления высказывани состоит из символов трех категорий:

1.

Символы первой категории: 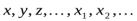Эти символы будем называть переменными высказываниями.

2.

Символы второй категории: 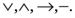они носят общее название логических связок. Первый из них – знак дизъюнкции или логического сложения, второй – знак конъюнкции или логического умножения, третий – знак импликации или логического следования и четвертый – знак отрицания.

3.

Третью категорию составляет пара символов ( ), называемая скобками.

Других символов исчисление высказываний не имеет.

^ Формулы исчисления высказываний представляют собой последовательности символов алфавита исчисления высказываний. Для обозначения формул будем пользоваться большими буквами латинского алфавита. Эти буквы не являются символами исчисления. Они представляют собой только условные обозначения формул.

Определение формулы исчисления высказываний.

1.

Всякая переменная 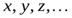является формулой.

2.

Если А и В- формулы , то слова 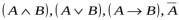- тоже формулы.

3.

Никакая другая строчка символов не является формулой.

Переменные высказывания будем называть элементарными формулами.

2. Следующим этапом в построении исчисления высказываний является выделение класса доказуемых (выводимых) формул.

Определение доказуемых формул имеет тот же характер , что и определение формулы.

Сначала определяются исходные доказуемые выводимые формулы (аксиомы), а затем определяются правила вывода, которые позволяют из имеющихся доказуемых формул получить новые доказуемые формулы.

Образование доказуемой формулы из исходных доказуемых формул путем применения правил вывода называется выводом (доказательством) данной формулы из аксиом.В основу исчисления высказываний могут быть положены различные системы аксиом, эквивалентные между собой в том смысле, что определяемый ими класс выводимых формул – один и тот же.

18

Вопрос 15. 1. Правила вывода. 2. Производные правила вывода.

1.Правило подстановки(ПП).

Если формула А выводима (доказуема) в исчислении высказываний, х- переменная, В- произвольная формула исчисления высказываний, то формула , полученная в результате замены в формуле А переменной х всюду , где она входит, формулой В, является также выводимой(доказуемой) формулой (ситуация та же, что имела место в алгебре логики, которая является интерпретацией исчисления высказываний).

Операция замены в формуле А переменной х формулой В, носит название подстановки и символически записывается так:

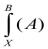или .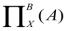

Уточним сформулированное правило:

а) если формула А есть собственно переменная х , то подстановка дает , очевидно, В;

б) если формула А есть переменная y , отличная от х ,то подстановка 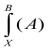дает А;

в)подстановка формулы В вместо х в отрицание формулы А есть отрицание подстановки , т. е. подстановка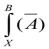

дает;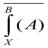

г) если А1 и А2- некоторые формулы, то подстановка 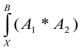дает 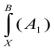*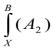, где через символ *

обозначен любой из символов операций конъюнкция, дизъюнкция или отрицание

Если А- выводимая (доказуемая ) формула, то будем писать, как и ранее, ├А. Тогда ПП можно записать схематически следующим образом:

├А____ .

├

И читается эта запись так: ―Если формула А выводима (доказуема), то выводима (доказуема) и формула

.

^ 2 Правило заключения (ПЗ).

Если формулы А и А→В выводимы (доказуемы) в исчислении высказываний, то формула В также выводима (доказуема). Схематическая запись этого правила имеет вид:

├А;├А→В (Modus ponens)

├В

Правомерность этого правила очевидна: если импликация и посылка истинны, то заключение в импликации может быть только истинным(см. таблицу истинности операции ―импликация‖).

19

2. Другим примером правил, с помощью которых можно, при необходимости вывести новые правила функциональной зависимости, являются так называемые производные правила вывода.

Что это за правила, как они получаются?

Известно, что если из одних правил, уже существующих, законными логическими методами вывести другие, то эти новые правила, называемые производными, можно использовать наряду с исходными правилами.

Необходимо специально отметить, что эти самые произвольные правила являются «производными» именно от пройденных нами ранее правил вывода Армстронга.

Сформулируем производные правила вывода функциональных зависимостей в виде следующей теоремы.

Теорема.

Следующие правила являются производными от правил вывода Армстронга.

Правило вывода 1. ├ X Z → X;

Правило вывода 2. X → Y, X → Z ├ X Y → Z;

Правило вывода 3. X → Y Z ├ X → Y, X → Z;

Здесь X, Y, Z, W, так же как и в предыдущем случае, – произвольные подсхемы схемы отношения S.

1. Первое производное правило называется правилом тривиальности и читается следующим образом:

«Выводится правило: ―объединение подсхем X и Z функционально влечет за собой X‖».

Функциональная зависимость с левой частью, являющейся подмножеством правой части, называется тривиальной. Согласно правилу тривиальности ограничения тривиальной зависимости выполняются автоматически.

Интересно, что правило тривиальности является обобщением правила рефлексивности и, как и последнее, могло бы быть получено непосредственно из определения ограничения функциональной зависимости. Тот факт, что это правило является производным, не случаен и связан с полнотой системы правил Армстронга. Подробнее о полноте системы правил Армстронга мы поговорим чуть позднее.

2.Второе производное правило называется правилом аддитивности и читается следующим образом: «Если подсхема X функционально определяет подсхему Y, и X одновременно функционально определяет Z, то из этих правил выводится следующее правило: ―X функционально определяет объединение подсхем Y и Z‖».

3.Третье производное правило называется правилом проективности или правилом «обращение аддитивности». Оно читается следующим образом: «Если подсхема X функционально определяет объединение подсхем Y и Z, то из этого правила выводится правило: ―X функционально определяет подсхему Y и одновременно X функционально определяет подсхему Z‖», т. е., действительно, это производное правило является обращенным правилом аддитивности.

Любопытно, что правила аддитивности и проективности применительно к функциональным зависимостям с одинаковыми левыми частями позволяют объединять или, наоборот, расщеплять правые части зависимости.

При построении цепочек вывода после формулировки всех посылок применяется правило транзитивности с той целью, чтобы включить функциональную зависимость с правой частью, находящейся в заключении.

Вопрос 16. 1.Понятие выводимости формулы из совокупности формул. 2.Понятие вывода. 3.Правила выводимости.

1. Будем рассматривать конечную совокупность формул Н={А1,А2,…,Аn}. Определение формулы, выводимой из совокупности Н.

1)Всякая формула Аi H ,является формулой, выводимой из Н.

20