
матлог
.pdfREADME, BEACH=))) Теоретические ответы на вопросы по матлогике. В содержании есть пара неполных ответов (7, 16), пара безответных вопроса(17, 31) и один пропущенный (27). Если есть жгучее и непреодолимое желание дополнить ответы на эти вопросы, то дописываем.
Вопрос 1. Задача и предмет логики. Алгебра логики. Понятие высказывания. (стр.2) Вопрос 2. Логические операции над высказываниями. (стр. 3)
Вопрос 3. Формулы алгебры логики. Равносильные формулы. Равносильные преобразования формул. (стр. 4) Вопрос 4. Алгебра Буля. Алгебра множеств. (стр. 7)
Вопрос 5. Операции над множествами. Свойства операций над множествами. (стр. 8) Вопрос 6. Декардово произведение множеств. (стр. 11)
Вопрос 7. Фун-ии алгебры логики. Представление произвольной фун-ии алгебры алгебры логики в виде формулы алгебры логики. (ответ неполон, но он есть) (стр. 11)
Вопрос 8. Закон двойственности. (стр. 15)
Вопрос 9. Дизъюнктивная нормальная форма и совершенная дизъюнктивная нормальная форма. (стр. 15) Вопрос 10. Конъюктивная нормальная форма и совершенная конъюктивная нормальная форма. (стр. 15) Вопрос 11. Проблема разрешимости. (стр. 15)
Вопрос 12. Релейно-контактные схемы. (стр. 16)
Вопрос 13. Исчисление высказываний. Система аксиом исчисления высказываний. (стр. 17)
Вопрос 14. Понятие формулы исчисления высказываний. Определение доказуемой формулы. (стр. 18) Вопрос 15. Правила вывода. Производные правила вывода. (стр. 19)
Вопрос 16. Понятие выводимости формулы из совокупности формул. Понятие вывода. Правила выводимости. (ответ не полон, но он есть) (стр. 20)
Вопрос 17. Доказательство некоторых законов логики. (нет ответа) (стр. 21)
Вопрос 18. Связь между алгеброй высказываний и исчислением высказываний. (стр. 21) Вопрос 19. Проблемы аксиоматического исчисления высказываний. (стр. 22)
Вопрос 20. Логика предикатов. Одноместные, двухместные и многоместные предикаты. (стр. 24) Вопрос 21. Логические операции над предикатами. Кванторные операции. (стр. 25)
Вопрос 22. Понятие формулы логики предикатов. Основные равносильности логики предикатов. (стр. 25) Вопрос 23. Предваренная нормальная форма. Общезначимость и выполнимость формул. (стр. 26)
Вопрос 24. Проблема разрешимости в логике предикатов. (стр. 27)
Вопрос 25. Запись математических предложений в виде формул логики предикатов. (стр. 27) Вопрос 26. Построение противоположных утверждений. (стр. 28)
Вопрос 27. отсутствует. (пропущен) (.i.)
Вопрос 28. Доказательство методом от противного. (стр. 29)
Вопрос 29. Замечания об аксиоматическом исчислении предикатов. (стр. 29) Вопрос 30. Понятие алгоритма и его характерные черты. (стр. 30)
Вопрос 31. Численные и логические алгоритмы. (нет ответа) (стр. 31)
Вопрос 32. Разрешимые и эффективно перечислимые множества. Теорема Поста. (стр. 31) Вопрос 33. Три направления в подходах к определению точного понятия алгоритма. (стр. 31)
Вопрос 34. Эффективно вычислимые, частично рекурсивные и общерекурсивные функции. Операции над функциями. Тезис Чѐрча. (стр. 31)
Вопрос 35. Машина Тьюринга. Устройство машины Тьюринга. Основная гипотеза теории алгоритмов. (стр. 33) Вопрос 36. Понятие нормальных алгоритмов Маркова. (стр. 34)
Вопрос 37. Неразрешимые алгоритмические проблемы. (стр. 35) Вопрос 38. NP-полнота. (стр. 35)
Автор: К. Мальцев
1
Вопрос 1. 1. Задача и предмет логики. 2. Алгебра логики. 3. Понятие высказывания.
1. Логика — одна из древнейших наук» возникла в рамках философии более 2300 лет назад в трудах древнегреческого философа Аристотеля, который впервые систематизировал формы и правила мышления.
Логика изучает мышление. Познание мира, как его отражение в сознании, осуществляется в двух формах: чувственное и абстрактное познание.
Символическая логика использует для анализа форм и законов мышления средства и методы, по традиции считающиеся принадлежащими математике.
Мышление изучается многими науками. Предметом изучения логики являются формы мышления, законы выводного знания, законы связи мыслей. Логика изучает формы правильного рассуждения. Традиционная формальная логика исследует законы связи между сложившимися мыслями, методы оперирования ими.
Логика мышления представляет собой определенный способ отражения действительности. Имен но соблюдение логических законов делает мышление правильным, т.е. способным при выполнении ряда условий достигать истинного знания. Таким образом, логика изучает то общее, что связывает мысли в их движении к познанию истины.
2.Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B,  ,
, 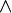 ,
, 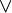 , 0, 1}, где B — непустое множество, над элементами которого определены три операции:
, 0, 1}, где B — непустое множество, над элементами которого определены три операции:
 отрицание (унарная операция),
отрицание (унарная операция),
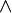 конъюнкция (бинарная),
конъюнкция (бинарная),  дизъюнкция (бинарная),
дизъюнкция (бинарная),
а также константы — логический ноль 0 и логическая единица 1.
Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например 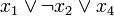 ). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например
). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например 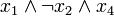 ).
).
3. Основным (неопределяемым) понятием математической логики является понятие «простого высказывания».
Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь»
Пpиведем пример высказываний:
1.Санкт –Петербург стоит на Неве
2.Париж — столица Англии
3.Карась не рыба
4.Число 6 делится на 2 и на 3
5.Если юноша окончил среднюю школу, то он получает аттестат зрелости,
высказывания 1), 4), 5) истинны, а высказывания 2) и 3) ложны.
Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием. Различают два вида высказываний:
Высказывание, представляющее собой одно утверждение, принято называть простым, или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).
Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если .... то ...», «тогда и только тогда», принято называть сложными, или составными.
Так, высказывание 3) получается из простого высказывания «Карась - рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на З», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если ..., то ...». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда».
В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Элементарные высказывания обозначаются малыми буквами латинского алфавита: х, у, z, ..., а, b, с, ...; истинное значение высказывания цифрой 1, а ложное значение - буквой цифрой 0.
Если высказывание а истинно, то будем писать а = 1, а если а ложно, то а = 0. Основные понятия:
2

Суждение — это некоторое высказывание, которое может быть истинным или ложным.
Утверждение — это суждение, которое требуется доказать или опровергнуть.
Рассуждение — это цепочка взаимосвязанных суждений, фактов, общих положений и умозаключений, получаемых из других суждений по определенным правилам вывода.
Дедукция — это рассуждения от общего к частному.
Индукция — это рассуждение от частного к общему.
Вопрос 2. Логические операции над высказываниями.
Логическая операция — это способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Во избежание неодинаковой трактовки смысла каждой из связок определим этот смысл следующими ниже таблицами.
1. Логическое отрицание (инверсия) образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что...» (см. табл. 1.2).
Обозначения логического отрицания: НЕ А, ¬А, NOT A, А'.
Таблица 1.2. Логическая связка ¬.
А |
¬A |
1 |
0 |
0 |
1 |
Из таблицы следует, что отрицание высказывания истинно, когда высказывание ложно, и ложно, когда высказывание истинно.
2. Логическое умножение (конъюнкция) образуется соединением двух высказываний в одно с помощью союза «и» (см.
табл. 1.3).
Обозначения логического умножения: А и B, А \/ В, А & В, А * В, A AND В.
Таблица 1.3. Логическая связка &.
А |
В |
А & В |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Из таблицы следует, что конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна тогда и только тогда, когда ложно хотя бы одно из высказываний.
3. Логическое сложение (дизъюнкция) образуется соединением двух высказываний в одно с помощью союза «или»
(см. табл. 1.4).
Обозначения логического сложения: А или B, А V B, А|В, А+В, A OR В.
Таблица 1.4. Логическая связка V
А |
В |
А V В |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
Из таблицы следует, что дизъюнкция двух высказываний истинна тогда и только тогда, когда хотя бы одно из высказываний истинно, и ложна тогда и только тогда, когда ложны оба высказывания,
3

4. Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи
«если то ...» (см. табл. 1.5).
Обозначения логического следования: А —>, А => В. Говорят: если А, то В; А влечѐт В; В следует из А.
Таблица 1.5. Логическая связка =>
А |
В |
A=>В |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Из таблицы следует, что импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное (когда истинная посылка влечѐт ложное заключение).
5. Логическое равенство (эквиваленция) образуется соединением двух высказываний с помощью оборота речи «тогда и только тогда, когда...» (см. табл. 1.6).
Обозначения логического следования: А ~ B, А <=> В, А = В. Говорят: А тогда и только тогда, когда В.
Таблица 1.6. Логическая связка <=>
А |
В |
A<=>В |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Вопрос 3. 1.Формулы алгебры логики. 2.Равносильные формулы. 3.Равносильные преобразования формул.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
0 |
|
x y |
|
x<y |
|
~x |
|
x>y |
|
~y |
|
x |
y |
|
x|y |
|
x&y |
|
x |
y |
|
y |
|
x |
y |
|
x |
|
x |
y |
|
x |
y |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
0 |
|
0 |
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
|
1 |
|
0 |
|
1 |
|
|
0 |
|
1 |
|
|
0 |
|
1 |
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
0 |
|
1 |
|
0 |
|
0 |
|
1 |
|
1 |
|
0 |
|
0 |
|
1 |
|
|
1 |
|
0 |
|
0 |
|
|
1 |
|
1 |
|
|
0 |
|
0 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
1 |
|
1 |
|
1 |
|
|
1 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1 |
|
1 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
1 |
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~(x & y) = x | y ~(x | y) = x & y ~(x > y) = x 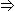 y ~(x
y ~(x  y) = x > y ~(x < y) = x
y) = x > y ~(x < y) = x 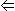 y ~(x
y ~(x  y) = x < y
y) = x < y
~(x 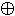 y) = x
y) = x  y ~(x
y ~(x  y) = x
y) = x 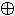 y ~(x
y ~(x 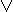 y) = x
y) = x  y ~(x
y ~(x  y) = x
y) = x 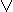 y
y
x & y = y & x
x 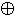 y = y
y = y 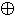 x x
x x 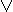 y = y
y = y 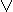 x
x
x  y = y
y = y  x
x
x  y = y
y = y  x x | y = y | x
x x | y = y | x
x > y = y < x x  y = y
y = y  x
x
4
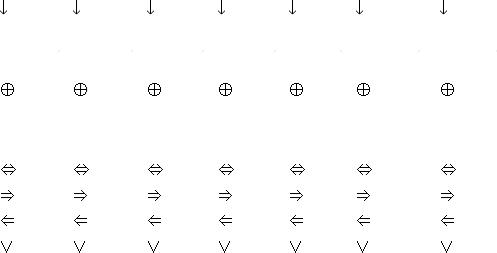
(x & y) & z = x & (y & z) (x 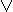 y)
y) 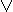 z = x
z = x 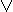 (y
(y  z)
z)
(x  y)
y) 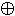 z = x
z = x 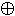 (y
(y  z) (x
z) (x  y)
y)  z = x
z = x  (y
(y  z)
z)
x & (y 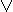 z) = (x & y)
z) = (x & y)  (x & z) (x
(x & z) (x 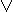 y) & z = (x & z)
y) & z = (x & z) 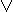 (y & z) x
(y & z) x 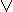 (y & z) = (x
(y & z) = (x  y) & (x
y) & (x 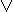 z) (x & y)
z) (x & y) 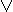 z = (x
z = (x 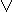 z) & (y
z) & (y  z)
z)
x & (y 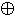 z) = (x & y)
z) = (x & y)  (x & z) (x
(x & z) (x  y) & z = (x & z)
y) & z = (x & z) 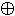 (y & z)
(y & z)
x 0 = ~x |
0 |
x = ~x |
x 1 = 0 |
1 |
x = 0 |
x x = ~x |
x ~x = 0 |
~x x = 0 |
|
|
|
|
|
|
|
||
x < 0 = 0 |
0 < x = x |
x < 1 = ~x |
1 < x = 0 |
x < x = 0 |
x < ~x = ~x |
~x < x = x |
||
|
|
|
|
|
|
|
||
x > 0 = x |
0 > x = 0 |
x > 1 = 0 |
1 > x = ~x |
x > x = 0 |
x > ~x = x |
~x > x = ~x |
||
|
|
|
|
|
|
|
|
|
x 0 = x |
0 |
x = x |
x 1 = ~x |
1 |
x = ~x |
x x = 0 |
x ~x = 1 |
~x x = 1 |
|
|
|
|
|
|
|
||
x | 0 = 1 |
0 | x = 1 |
x | 1 = ~x |
1 | x = ~x |
x | x = ~x |
x | ~x = 1 |
~x | x = 1 |
||
|
|
|
|
|
|
|
||
x & 0 = 0 |
0 & x = 0 |
x & 1 = x |
1 & x = x |
x & x = x |
x & ~x = 0 |
~x & x = 0 |
||
|
|
|
|
|
|
|
|
|
x 0 = ~x |
0 |
x = ~x |
x 1 = x |
1 |
x = x |
x x = 1 |
x ~x = 0 |
~x x = 0 |
|
|
|
|
|
|
|
|
|
x 0 = ~x |
0 |
x = 1 |
x 1 = 1 |
1 |
x = x |
x x = 1 |
x ~x = ~x |
~x x = x |
|
|
|
|
|
|
|
|
|
x 0 = 1 |
0 |
x = ~x |
x 1 = x |
1 |
x = 1 |
x x = 1 |
x ~x = x |
~x x = ~x |
|
|
|
|
|
|
|
|
|
x 0 = x |
0 |
x = x |
x 1 = 1 |
1 |
x = 1 |
x x = x |
x ~x = 1 |
~x x = 1 |
|
|
|
|
|
|
|
|
|
~(x & y) = ~x 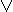 ~y ~(x
~y ~(x 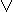 y) = ~x & ~y
y) = ~x & ~y
x  y = (x
y = (x  y) & (x
y) & (x  y) x
y) x 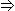 y = y
y = y 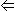 x
x
x 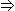 y = ~x
y = ~x 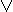 y x
y x 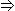 y = ~y
y = ~y 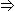 ~x
~x
x > y = x & ~y x < y = ~x & y
x 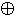 y = (x & ~y)
y = (x & ~y)  (~x & y)
(~x & y)
x  y = ~x & ~y = ~(x
y = ~x & ~y = ~(x 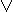 y)
y)
x  y = (x & y)
y = (x & y) 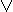 (~x & ~y) x
(~x & ~y) x 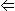 y = x
y = x 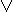 ~y
~y
x  y = ~x
y = ~x 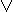 y
y
x | y = ~x 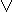 ~y = ~(x & y)
~y = ~(x & y)
x 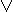 y = ~(~x & ~y) x & y = ~(~x
y = ~(~x & ~y) x & y = ~(~x 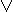 ~y)
~y)
~x = x | x
x 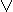 y = (x | x) | (y | y) ~x = x
y = (x | x) | (y | y) ~x = x 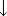 x
x
x & y = (x  x)
x)  (y
(y  y)
y)
~x = x 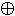 1
1
x  y = x
y = x 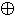 y
y 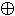 (x & y)
(x & y) 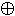 1 x
1 x 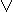 y = x
y = x 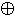 y
y 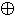 (x & y)
(x & y)
x | y = (x & y) 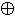 1 x
1 x  y = x
y = x 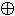 y
y 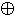 1 x > y = x
1 x > y = x 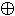 (x & y)
(x & y)
5
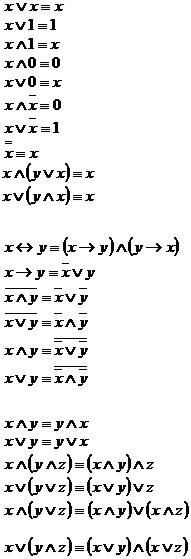
x  y = x
y = x 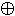 (x & y)
(x & y) 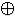 1 x < y = y
1 x < y = y 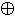 (x & y)
(x & y)
x  y = y
y = y 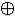 (x & y)
(x & y) 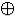 1
1
2. Определение. Пусть f и g — две формулы, а A1,...,Ап — все высказывательные переменные, входящие в запись хотя бы одной из этих формул. Общей логической возможностью формул f и g называется всякий набор конкретных значений истинности для высказывательных переменных A1,...,Ап .
Можно определить понятие общей логической возможности для любого конечного числа формул.
Определение. Две формулы f и g называются равносильными: f=g, если во всякой общей для f u g логической возможности f и g принимают одинаковые значения т.е. таблицы истинности одинаковы.
3. Определение 1. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в них высказываний
(А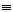 В).
В).
Важнейшие равносильности можно разбить на три группы: I. Основные равносильности:
1.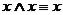 законы
законы
2. |
идемпотентности. |
3. |
|
4. |
|
5. |
|
6. |
|
7. |
- закон противоречия. |
8. |
- закон исключенного третьего. |
9.- закон снятия двойного отрицания.
10. |
законы |
11. |
поглощения. |
|
II. Равносильности, выражающие одни логические операции через другие: |
1. |
|
2. |
|
3. |
законы |
4. |
де Моргана. |
5. |
|
6. |
|
|
III. Равносильности, выражающие основные законы алгебры логики: |
1. |
- коммутативность конъюнкции. |
2. |
- коммутативность дизъюнкции. |
3. |
- ассоциативность конъюнкции. |
4. |
- ассоциативность дизъюнкции. |
5. |
- дистрибутивность конъюнкции относительно |
|
дизъюнкции. |
6. |
- дистрибутивность дизъюнкции относительно |
|
конъюнкции. |
Используя равносильности группы I, II и III, можно часть формул алгебры логики или всю формулу заменить равносильной ей формулой. Такие преобразования называются равносильными. Равносильные преобразования формул применяются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
6
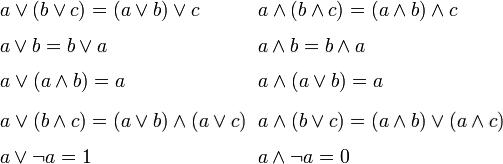
Вопрос 4. 1.Алгебра Буля. 2. Алгебра множеств.
1. Булевой алгеброй называется непустое множество A с двумя бинарными операциями 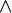 (аналог конъюнкции),
(аналог конъюнкции), 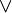 (аналог дизъюнкции), унарной операцией
(аналог дизъюнкции), унарной операцией  (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
(аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
ассоциативность
коммутативность
законы поглощения
дистрибутивность
дополнительность
2. R – множество действительных чисел.
X 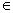 R – элемент X принадлежит множеству R.
R – элемент X принадлежит множеству R.
!Равные множества – множества, состоящие из одинаковых элементов.
A = B – множество А равно множеству B.
Ø– пустое множество.
a 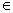 A – элемент a принадлежит множеству A
A – элемент a принадлежит множеству A
A 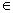 A - множество А принадлежит семейству A
A - множество А принадлежит семейству A
A 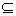 C – Множество А является подмножеством множества С.
C – Множество А является подмножеством множества С.
A  C – Множество А строго является подмножеством множества С.
C – Множество А строго является подмножеством множества С.
Если А ≠ С и А 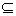 C, то А
C, то А 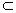 С. (строго).
С. (строго).
Если A  C и C
C и C  А, то А = С.
А, то А = С.
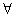 A: A
A: A 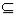 A
A
Ø A – несобственные подмножества
A – несобственные подмножества
!Множество объект неупорядочен
!Пустое множество Ø является подмножеством любого множества.
!Существуют конечные и бесконечные множества. Пусть n – число элементов данного множества А. Это число называется мощностью данного множества.
7
!У множества рациональных чисел мощность является счетной (т.е. все элементы можно пронумеровать).
!У множества иррациональных чисел мощность – континиум. Обозначается (С).
{1;2;3} = {2;1;3} (1,2,3) ≠ (2,1,3)
Вопрос 5. 1.Операции над множествами. 2.Свойства операций над множествами.
Операции над множествами (свойства включительно)
8

Объединение
Определение
Пусть даны два множества A и B.
Тогда их объединением называется множество
Примеры
Пусть A = {1,2,3,4},B = {3,4,5,6,7}. Тогда
Свойства
Объединение множеств является бинарной операцией на произвольном булеане 2X;
Операция объединения множеств коммутативна:
Операция объединения множеств транзитивна
(ассоциативность): 
Пустое множество X является нейтральным элементом операции объединения множеств: 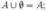
Таким образом булеан вместе с операцией объединения множеств является моноидом;
Операция пересечения множеств идемпотентна: 
Пересечение
Определение
Пусть даны два множества A и B.
Тогда их пересечением называется множество
! Гораздо реже используется обозначение AB.
Примеры
Пусть A = {1,2,3,4},B = {3,4,5,6}. Тогда
Свойства
Пересечение множеств является бинарной операцией на произвольном булеане 2X;
Операция пересечения множеств коммутативна:
Операция пересечения множеств транзитивна
(ассоциативность): 
Универсальное множество X является нейтральным элементом операции пересечения множеств:
Таким образом булеан вместе с операцией пересечения множеств является абелевой группой;
Операция пересечения множеств идемпотентна:
Если  — пустое множество, то
— пустое множество, то 
9

Дополнение
Определение
Пусть даны два множества A и B. Тогда их (теоретикомножественная) разность определяется следующим образом:
Примеры
Пусть 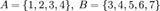 . Тогда
. Тогда
Пусть  — множество всех вещественных чисел,
— множество всех вещественных чисел,  — множество рациональных чисел, а
— множество рациональных чисел, а  — множество целых чисел. Тогда
— множество целых чисел. Тогда  — множество всех иррациональных чисел, а
— множество всех иррациональных чисел, а  — дробных.
— дробных.
Свойства
Пусть A,B,C — произвольные множества. Тогда
Симметрическая разность
Определение
Пусть даны два множества A и B. Тогда их симметрической разницей называется множество:
Примеры
Пусть A = {1,2,3,4,5},B = {3,4,5,6,7}. Тогда
A B = {1,2,6,7}.
Свойства
Симметрическая разность может быть эквивалентно определена следующим образом:
Симметрическая разница является бинарной операцией на любом булеане;
Симметрическая разность коммутативна: A B =
B A;
Симметрическая разность транзитивна: (A B)ΔC =
AΔ(B C);
Пустое множество является нейтральным элементом симметрической разности: 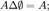
Любое множество обратно само себе относительно операции симметрической разности: 
В частности, булеан с операцией симметрической разности является абелевой группой;
Булеан с операцией симметрической разности также является векторным пространством над полем 
Пересечение множеств дистрибутивно относительно симметрической разности:
В частности, булеан с операциями пересечения множеств и симметрической разности является алгеброй с единицей.
10
