МВ (методичка)

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования

«Уральский государственный университет им. А.М. Горького»

ИОНЦ «Бизнес - информатика»

Математико-механический факультет

Кафедра вычислительной математики

МЕТОДЫ ВЫЧИСЛЕНИЙ В ЭКОНОМИЧЕСКОМ МОДЕЛИРОВАНИИ

Учебно-методическое пособие

Екатеринбург

2007

Методическое пособие подготовлено кафедрой вычислительной математики

Данное пособие предназначено для студентов специальности «Бизнес – информатика» дневной формы обучения. В нем рассматриваются актуальные экономические модели, их реализация с помощью математических методов. Приведен необходимый минимум теоретического материала по курсу «Численные методы» и рассмотрено достаточное количество примеров, что поможет студентам в самостоятельной работе по освоению данного курса и будет полезно при выполнении лабораторных работ.

© Коврижных А.Ю, Конончук Е.А., Лузина Г.Е.	2

Введение.

Моделирование является одним из методов научного познания. Математическая модель позволяет экономить материальные ресурсы и предоставляет возможность изучать поведение системы в заданных экспериментатором условиях. Использование математических методов в экономике восходит к работам Ф. Кенэ («Экономическая таблица»), А. Смита (классическая макроэкономическая модель), Д. Риккардо (модель международной торговли). Моделированию рыночной экономики посвящены работы Л. Вальраса, О. Курно, В. Парето. С применением математических методов связаны работы В.В. Леонтьева, Р. Солоу, П. Самуэльсона, Д. Хикса, В.С Немчинова, В.В Новожилова, Л.В. Канторовича и многих других выдающихся ученых.

Примерами экономических моделей являются являются модели фирмы, модели экономического роста, модели потребительского выбора, модели равновесия на финансовых и товарных рынках. Построение экономической модели требует выполнения ряда шагов. Сначала формулируется предмет и цель исследования. Затем экономисты выявляют структурные и функциональные элементы модели, взаимосвязи между ними, существенные факторы, отвечающие цели исследования и отбрасывают то, что несущественно для решения задачи. На заключительном этапе проводятся расчеты по математической модели и анализ полученного решения. Именно на завершающем этапе применяются численные методы.

0.Математические модели в экономике

В данном разделе на материале ряда экономических моделей иллюстрируется применение методов численного решения нелинейных уравнений, систем алгебраических уравнений, численного интегрирования и методов решения дифференциальных уравнений.

0.1. Статические балансовые модели

Системы линейных алгебраических уравнений применяются в макроэкономике для проведения балансового анализа многоотраслевого хозяйства. Цель балансового анализа — ответить на вопрос, каким должен быть объем производства каждой из отраслей хозяйства, чтобы удовлетворить все потребности в продукции этой отрасли? Предполагается, что каждая отрасль выступает одновременно как производитель некоторого вида продукции и как потребитель продукции других (в том числе своей) отраслей. Процесс производства рассматривается за некоторый период времени, например, за год.

Предположим, что производственная сфера хозяйства состоит из n отраслей. Каждая из этих отраслей производит однородный продукт. Часть продукции идет на производственное потребление данной отраслью и другими отраслями, а другая часть предназначена для потребления вне сферы ма-

териального производства. Далее примем следующие обозначения: xi — общий объем продукции i –

йотрасли (или её валовой объем), i=1,2,…,n; xij — объем продукции i – й отрасли, потребляемый j –

йотраслью в процессе производства, i,j=1,2,…,n; yi — объем продукции i – й отрасли, предназна-

3

ченный к потреблению в непроизводственной сфере (объём конечного потребления). В этот объём входят личное потребление граждан, создаваемые хозяйственные запасы, экспорт, инвестиции, обес-

печение общественных потребностей. Уравнения баланса выражают тот факт, что валовой выпуск xi

расходуется на производственное потребление, равное хi1 + хi2 +... + хin и непроизводственное по-

требление, равное yi . Таким образом, имеем

n
xi = ∑хij + yi , i =1,..., n .	(0.1.1)

j =1

В зависимости от того, в каких единицах измерения записываются соотношения баланса, различают натуральный или стоимостной межотраслевые балансы.

Рассмотрим величины

aij = xxij , i, j =1,...,n , (0.1.2)

j

которые называют коэффициентами прямых затрат. Дело в том, что эти величины остаются постоянными в течение ряда лет, поскольку технологии производства также остаются постоянными или мало меняются за указанный промежуток времени. На это важное обстоятельство было указано В. Леонтьевым при исследовании развития американской экономики в предвоенный период.

Согласно предположению (0.1.2) уравнения (0.1.1) принимают вид

n

xi = ∑aij xj

+ yi ,

i =1, 2,..., n .

(0.1.3)

j=1

Записывая (0.1.3) в матричной форме получаем

x = Ax + y ,

(0.1.4)

где

a11

a12

...

a1n

x1

y1

a

a

...

a

,

x =

x

,

y

A =

21

21

...

2n

2

y =

2

.

... ...

...

...

...

a

a

...

a

x

y

n

n1

n2

nn

n

Обозначая символом E - единичную матрицу, получаем

(E − A)x = y .

(0.1.5)

Если существует обратная матрица (E − A)−1 , то из (0.1.5) следует равенство

x = (E − A)−1 y .

(0.1.6)

Решение системы (0.1.4) требует применения численных методов.

Из экономического смысла задачи вытекает, что все компоненты матрицы A и вектора y яв-

ляются неотрицательными ( A ≥ 0 , y ≥ 0 ). Все компоненты вектора x также должны быть неотрица-

тельны ( x ≥ 0 ).

4

Матрица A называется продуктивной, если для любого вектора y ≥ 0 существует решение

x ≥ 0 уравнения (0.1.4). При этом модель Леонтьева называется продуктивной. Справедливы следующие критерии.

1) Матрица A ≥ 0 продуктивна тогда и только тогда, когда матрица (E − A)−1 существует и

неотрицательна.
2) Матрица A ≥ 0 продуктивна тогда и только тогда, когда сходится бесконечный ряд
E + A + A2 +....	(0.1.7)
Доказывается, что если бесконечный ряд (из матриц)
E + A + A2 +...

сходится, то его сумма есть матрица (E − A)−1 . Отметим, что если сумма элементов любого столбца неотрицательной матрицы меньше 1, то матрица А продуктивна. Действительно, пусть q – наиболь-

шая из указанных сумм, q <1 . Тогда все элементы матрицы не превосходят q. Оценим элемент мат-

рицы A2

(A2 )ij = ai1a1 j +ai2a2 j +...+ ainanj ≤ q2 .

Аналогично получаем, что (A3 )ij ≤ q3 , и т.д. Значит ряд (0.1.7) сходится и матрица A продуктивна.

0.2. Некоторые модели экономической динамики

Динамические модели характеризуют изменение экономических процессов во времени. Моделирование может осуществляться с использованием дискретного и непрерывного подхода. В настоящем разделе даются два примера такого моделирования. Эти примеры являются абстрактными. Однако в рассматриваемых случаях их решение может быть найдено в явном виде, что позволяет проанализировать особенности поведения решения для различных случаев соотношения параметров моделирования.

Паутинообразная модель рынка

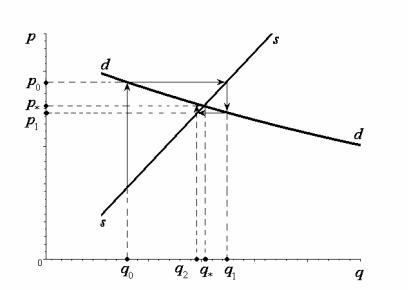
Эта модель объясняет феномен регулярно повторяющихся циклов изменения объемов продажи и цен товаров на рынке. Хорошо известно, что основными категориями рыночных отношений являются спрос и предложение. Эти категории зависят от многих факторов, главным из которых является цена товара. Примем обозначения. Пусть p – цена товара (от английского price - цена), d –объем спроса (demand – спрос), s – предложение (supply). Предполагаем, что s(p) и d(p) являются непрерыв-

ными функциями, при этом, если цена p – мала, то d( p) − s( p) > 0 (спрос превышает предложение),

а при больших ценах d( p) −s( p) < 0 и предложение превышает спрос. При данных предположения существует равновесная цена p* , удовлетворяющая равенству d ( p* ) = s( p* ) .

Паутинная модель рынка – простейшая модель поиска равновесной цены. Отметим сразу, что с математической точки зрения, решение уравнения

5

					d( p) = s( p)				(0.2.1)
может быть проведено методом простой итерации при сведении его к виду
					p =ϕ( p)				(0.2.2)
и получению последовательных приближений
					pn =ϕ( pn ),			n =1,2,... .	(0.2.3)
Так, если ϕ( p)	- дифференцируемая функция и		′		<1, то lim p		= p . Однако, переход от урав-
			ϕ ( p)			n
					n→∞			*

нения (0.2.1) к уравнению (0.2.2) может быть осуществлен множеством способов, и теперь уравнение (0.2.2) представляет собой описание модели рынка с уже другими функциями спроса и предложения d( p) = p , s( p) =ϕ( p) , хотя и с той же равновесной ценой p* . Поэтому, такой подход целесообра-

зен лишь для поиска равновесной цены, но не является приемлемым для исследования циклов изменения объемов продажи и цен исходной модели с уравнением (0.2.1).

Предположим, производители определяют величину объема производства (предложение объема товара) в текущем году на основе цен, установившихся в предшествующем периоде. Например, площадь, отводимую под посев зерновых культур, выбирают в зависимости от цены, сложившейся в предыдущем году. Таким образом, в функции предложения должен быть учтен временной лаг продолжительностью в единицу времени (в данном случае год). Действительно, предложение появится на рынке по окончании данного цикла, т.е., через год после принятия решения. Согласно данным предположениям опишем динамику цены уравнениями

qs = s ( p		), qd	= d	( p ),	qd	= qs ,	(0.2.4)
t	t t −1	t	t	t	t	t

где первое из уравнений как раз учитывает временной лаг в предложении. Справедливо равенство

dt ( pt ) = st ( pt −1) .

(0.2.5)

Проиллюстрируем применение данного подхода на конкретных примерах. Пусть теперь заданы функции

s( p) =ψ( p) ,	(0.2.6)
d( p) = c −ep ,	(0.2.7)

где ψ( p) - заданная непрерывная функция, c > 0, e > 0 - заданные параметры, такие, что существу-

ет равновесная цена p* . Следуя уравнениям (0.2.4) - (0.2.5) динамики построим последовательности

{qn } и {pn }(здесь n = t и обозначает дискретные моменты времени). Построение будет происходить рекуррентно в согласии с (0.2.6) – (0.2.7), и выбранным начальным значением q0 по следующим формулам:

p0 = d −1 (q0 ) = c −eq0 ,

q1 = s( p0 ) =ψ( p0 ) =ψ(d −1 (q0 )) =ψ c −eq0 ,

6

c

−q

(q ) = c −q1 =

c −ψ

0

e

p

= d −1

,

1

1

e

e

c −q

c −ψ

0

q2 = s( p1 ) =ψ

e

,

e

c −q

c −ψ

0

e

c −ψ

e

c

−q2

p2 = d

−1

(q2 )

=

=

,

e

e

и так далее. Возможные значения qi и

pi ,

i =1, 2,...показаны на рисунке 1.

Рис.0.1

Предположим, что

s( p) = a +bp ,

тогда рекуррентные соотношения, приведенные выше, позволяют получить явные формулы для эле-

ментов qi , i =1, 2,...:

q1 = a +lc −lq0 ,			l = b / e,
q	2	= (a +lc)(1−l) + q l2 ,
			0
q = (a +lc)(1−l +l2 ) +q l3				,
3			0
q = (a +lc)(1−l +l2			−l3 ) +q l4		,
4			0

и, наконец,

7

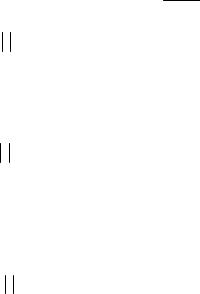
qn = (a +lc)(1−l +l2 +...+(−1)n−1ln−1 ) +(−1)n q0ln =

(a +lc)1−(−+1)n ln +(−1)n q0ln . 1 l

При этом справедливо равенство pn = c −eqn . Возможны случаи.

1) Если l <1, то справедливо равенство

lim q	n	=	(a +lc)	= q .
n→∞			1+l	*

Вэтом случае равновесие является устойчивым.

2)При l =1 получаем

q1 = a +c −q0 ,	q2 = q0 ,
q3 = a +c −q0 ,	q4 = q0 ,

итак далее. Здесь значенияqi чередуются вокруг равновесного состояния.

3)Если l >1, то {qn } расходится и равновесие не является устойчивым.

Дифференциальные уравнения в экономической динамике

Рассмотрим простейшие модели экономического роста.

Пусть некоторая отрасль производит продукцию, объём которой x(t) реализуется к моменту времени t. Предположим, что вся продукция реализуется по фиксированной цене p (рынок в этом случае ненасыщаем). Тогда доход отрасли к моменту времени t составит

X (t) = px(t).

(0.2.8)

Далее обозначим символом I(t) величину инвестиций и предположим, что скорость выпуска продукции пропорциональна величине инвестиций

′	(0.2.9)
x (t) = sI (t) .
При этом величина инвестиций есть фиксированная часть дохода, а значит
I (t) = mX (t) = mpx(t) .	(0.2.10)

Здесь m – норма дохода инвестиций, постоянная величина, 0 < m <1.

Непосредственно из (0.2.9) с учетом (0.2.8) и (0.2.10) получаем дифференциальное уравнение

′	(0.2.11)
x (t) = kx(t), k = smp .
Решение этого уравнения можно найти по формуле
x(t) = x0 exp(k(t −t0 )), x0 = x(t0 ) .
В условиях конкурентного рынка естественно предполагать, что кривая спроса	p = p(x) яв-

ляется функцией убывающей. Действительно, с увеличением объема произведенной продукции её цена падает в результате насыщения рынка. Получаем уравнение

8

	x′ = smp(x)x, x > 0, p(x) > 0			(0.2.12)
	После разделения переменных получаем
	x	dx
	∫		= sm(t −t0 ) .	(0.2.13)
		p(x)x
	x0

Аналитически вычислить интеграл в (0.2.13) не всегда представляется возможным (все зависит от ви-

да функции p = p(x) ). Это означает, что при решении уравнения (0.2.12) в общем случае, необходи-

мо применять численные методы интегрирования.

Проанализируем поведение решения x = x(t) уравнения (0.2.12). Дифференцируя по времени,

имеем

dp
x′′ = smx′		x + p(x) .	(0.2.14)
dx

Принимая во внимание определение эластичности спроса относительно цены, которое задается формулой

E p (x) =

p dx

,

x dp

запишем (0.2.14) в виде

1

x

′′

′

= smx p

E p (x)

+1 .

(0.2.15)

Условие x′′ = 0 означает, что E p (x) = −1. Возможны случаи:

1)

E p (x)

>1,

x′′ > 0 - спрос эластичен.

2)

E p (x)

<1 ,

x′′ < 0 - спрос не эластичен.

Рис.0.2

Решение уравнения (0.2.15) изображается логистической кривой (см. Рис.0.2).

9

0.3. Методы вычислений в финансовых расчетах.

Рассмотрим ряд примеров из финансовой математики, где требуется применение методов вычислений.

Определение уровня процентной ставки.

Пусть в течение n лет фирма перечисляет в банк p раз в году средства в размере R/p денежных единиц (R – величина суммарного годового платежа) с целью создания фонда накопления. Банк начисляет проценты на данные взносы m раз в году по сложной процентной ставке j. Определим наращенную сумму (величину фонда накопления) такого потока платежей на момент окончания выплат. Вычислим

R

R

j m

1

R

j m

2

R

j m

np−1

S =

p

p

p

+

1

+

+

1

+

+...+

1

+

.

p

p

p

p

m

m

m

Данная сумма представляет собой сумму геометрической прогрессии с первым элементом

x = R
1		p
и знаменателем
			m
		j p
q = 1	+		.
		m

Применяя формулу суммы первых n членов геометрической прогрессии, получаем

m np

j p

mn

1−

1

+

j

1−q

np

R

m

R

1− 1

+

S = x

=

=

m

m

m

1

1−q

p

p

j

p

j p

1−

1+

1− 1

+

m

m

Предположим теперь, что величины S, R, p, m, n известны, требуется найти уровень процентной ставки j, обеспечивающий создание фонда накопления при данных параметрах сделки. Для этого требуется решить нелинейное уравнение

Φ(S, R, p, m, n, j) = 0 ,

где
						j mn
	R	1− 1		+
Φ(S, R, p, m, n, j) = S −					m						.
	p								m
						j p
		1− 1+
						m

Уравнение решается с использованием численных методов.

10