
матлог
.pdf2)Всякая доказуемая формула выводима из Н.
3)Если формулы С и С→В выводимы из совокупности Н, то формула В также выводима из Н. Если некоторая формула В выводима из совокупности Н, то это записывают так: Н├В.
Нетрудно видеть, что класс формул, выводимых из совокупности Н, совпадает с классом доказуемых формул
вслучае, когда совокупность Н содержит только доказуемые формулы, и в случае, когда Н пуста.
Если же совокупность формул Н содержит хотя бы одну не доказуемую формулу, то класс формул, выводимых из Н, шире класса доказуемых формул.
Пример.
Доказать, что из совокупности формул Н={А ,В} выводима формула A B . Так как А H и В H , то по определению выводимой формулы
Н├А, |
|
(1) |
Н├В. |
|
(2) |
|
A,B, A |
B, A |
Возьмем аксиомы 3 и 1 , и выполним подстановки |
( 3 ) и |
( 1 ) . |
|
X ,Y ,Z |
X ,Y |
В результате получим доказуемые формулы, которые выводимы из Н по определению выводимой формулы, т.
е. |
|
|
|
|
|
|
|
|
Н├(А→А)→((А→В)→(А A B )), |
|
|
|
|
(3) |
|||
Н├В→(А→В), |
|
|
|
|
|
|
(4) |
|
Так как формула А→А доказуема, то Н├А→А. |
|
|
|
(5) |
||||
Из |
формул |
(5) |
и |
(3) |
по |
правилу |
заключения |
получаем: |
Н├(А→В)→(А A B )). |
|
|
|
|
|
|
(6) |
|
Из формулы (2) и (4) по правилу заключения получаем: |
|
Н├А→В. |
(7) |
|
||||
Из формул (7) и (6) по правилу заключения получаем: |
|
Н├А A B . |
(8) |
|
||||
И, наконец, из формул (1) и (8) получаем: |
|
|
|
|
|
|||
|
Н├ A B |
|
|
|
|
|
|
(9) |
Ясно, что при доказательстве выводимости формулы из совокупности формул можно пользоваться не только основным правилом заключения, но и правилом сложного заключения. Тогда, пользуясь этим правилом , предложение (9) можно получить из предложений (5), (7), (1) и (3).
2.Выводом из множества гипотез (посылок, допущений) называется непустая конечная последовательность формул, в которой каждая формула есть или одна из гипотез, или формула, полученная из предшествующих формул последовательности по одному из правил вывода первого рода, или теорема (это понятие определяется ниже), если при построении этой последовательности ни одна переменная не отмечает сама себя (непосредственно или по транзитивности) и ни одна переменная не оказывается безотносительно отмеченной дважды; вывод является выводом последней формулы этой последовательности, называемой заключением, из исходного множества гипотез.
Пусть Г — множество гипотез; В — последняя формула по-следовательности формул, являющейся выводом. Факт наличия вывода формулы В из множества гипотез Г записывается так: Г |— В. Последнее выражение называется утверждением о выводимости (или выводимостью, или непосредственно обосно¬ванной выводимостью) формулы В из множества гипотез Г.
При осуществлении вывода справа от него будем писать его анализ, т.е. указывать, на каком основании каждая из формул введена в вывод, например, по какому правилу и из каких формул она получена, а также, указывать сведения, касающиеся отмечивания переменных.
Чаще всего бывает удобно в начале последовательности, являющейся выводом, выписать все гипотезы. Это, однако, не обязательно. Гипотезы можно выписывать по мере надобности, причем из определения вывода следует, что одна и та же гипотеза может встречаться в выводе несколько раз. Некоторые из гипотез вообще могут не встречаться в выводе. Проиллюстрируем это на примере.
Здесь ПД — правило дедукции, ДОП — доказательство от противного, СА — сведение к абсурду. Буквы А и В в формулировке правил обозначают формулы, а Г — множество формул (возможно, пустое). Эти правила представляются естественными, их, а также все правила первого рода следует запомнить и использовать не только при письменном, но и при неписьменном анализе рассуждений.
3.???????????????????? Нет ответа
Вопрос 17. Доказательство некоторых законов логики.
Нет ответа.
Вопрос 18. Связь между алгеброй высказываний и исчислением высказываний.
Формулы исчисления высказываний можно интерпретировать как формулы алгебры высказываний. Для этого будем трактовать переменные исчисления высказываний как переменные алгебры высказываний, т. е. переменные в
21
содержательном смысле, принимающие два значения: истина и ложь (1 и 0).
Операции 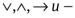 определим так же, как в алгебре высказываний.
определим так же, как в алгебре высказываний.
При этом всякая формула исчисления высказываний при любых входящих в нее переменных будет принимать одно из значений 1 или 0, вычисляемое по правилам алгебры высказываний.
Введем понятие значения формулы исчисления высказываний. Пусть А- формула исчисления высказываний, х1,х2,…,хn- попарно различные переменные, среди которых находятся все переменные, входящие в формулу А. Обозначим через а1, а2,…,аn набор значений этих переменных, состоящих из 1 и 0, длины n. Очевидно, что вектор (а1, а2,…,аn) имеет 2n значений.
Имеют место три теоремы, которые устанавливают связь между основными фактами алгебры высказываний и исчисления высказываний.
Теорема 1.
Каждая формула, доказуемая в исчислении высказываний, является тождественно истинной в алгебре высказываний.
Формулировка этой теоремы содержит в себе три положения:
1)Каждая аксиома исчисления высказываний – тождественно истинная формула в алгебре высказываний.
2)Правило подстановки, примененное к тождественно истинным формулам, приводит к тождественно истинным формулам.
3)Правило заключения, примененное к тождественно истинным формулам, приводит к тождественно истинным формулам.
Теорема 2.( о выводимости).
Пусть А –некоторая формула исчисления высказываний; х1,х2,…,хn – набор переменных, содержащих все переменные, входящие в формулу А; а1, а2,…,аn – произвольный фиксированный набор значений этих переменных. Обозначим через Н конечную совокупность формул
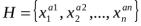 , где
, где 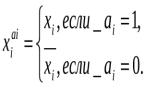 Тогда:
Тогда:
1.
Если Ra1,a2,..,an(A)=1, то H├A .
2.
Если Ra1,a2,..,an(A)=0, то H├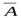 , где Ra1,a2,..,an(A)–значение формулы А на наборе а1, а2,…,аn.
, где Ra1,a2,..,an(A)–значение формулы А на наборе а1, а2,…,аn.
Теорема 3.
Каждая тождественно истинная формула алгебры высказываний доказуема в исчислении высказываний.
Вопрос 19. Проблемы аксиоматического исчисления высказываний.
Всякая аксиоматическая теория для ее обоснования требует рассмотрения четырех проблем:
1.
проблемы разрешимости,
2.
проблемы непротиворечивости,
3.
проблемы полноты,
4.
проблемы независимости.
22
Проблема разрешимости исчисления высказываний.
Проблема разрешимости исчисления высказываний заключается в доказательстве существования алгоритма, который позволил бы для любой заданной формулы исчисления высказываний определить, является ли она доказуемой или не является.
Имеет место теорема: проблема разрешимости для исчисления высказываний разрешима.
Действительно, любая формула исчисления высказываний может рассматриваться как формула алгебры высказываний, и, следовательно, можно рассматривать ее логические значения на различных наборах значений входящих в нее переменных.
Пусть А – любая формула исчисления высказываний, а х1,х2,…,хn – перечень входящих в нее переменных. Вычислим
Ra1,a2,..,an(A) на всех наборах значений а1, а2,…,аn входящих в нее переменных. Если при этом Ra1,a2,..,an(A)=1, на всех наборах а1, а2,…,аn, то формула А – тождественно истинна, и, значит, по теореме о доказуемости тождественно
истинной формулы она доказуема.
Если же существует набор значений переменных 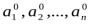 такой, что
такой, что 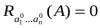 , то формула А – не тождественно истинная, и, значит, по теореме 1 §8 она не доказуема.
, то формула А – не тождественно истинная, и, значит, по теореме 1 §8 она не доказуема.
2. Проблема непротиворечивости исчисления высказываний.
Логическое исчисление называется непротиворечивым, если в нем не доказуемы никакие две формулы, из которых одна является отрицанием другой.
Иначе говоря, аксиоматическое исчисление называется непротиворечивым, если в нем не существует такая формула А,
что доказуема как формула А, так и формула  .
.
Проблема непротиворечивости заключается в выяснении вопроса: является данное исчисление непротиворечивым или нет?
Если в исчислении обнаруживаются доказуемые формулы вида А и 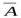 , то такое исчисление называется противоречивым. В рассмотренном нами исчислении высказываний невозможно вывести одновременно формулы А и
, то такое исчисление называется противоречивым. В рассмотренном нами исчислении высказываний невозможно вывести одновременно формулы А и
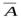 , т.е. это исчисление высказываний непротиворечиво.
, т.е. это исчисление высказываний непротиворечиво.
3.Проблема полноты исчисление высказываний.
Определение 1.
Аксиоматическое исчисление высказываний называется полным в узком смысле, если добавление к списку его аксиом любой недоказуемой в исчислении формулы в качестве новой аксиомы приводит к противоречивому исчислению.
Определение 2.
Исчисление высказываний называется полным в широком смысле, если любая тождественно истинная формула в нем доказуема.
Из этих определений следует, что проблема полноты исчисления высказываний содержит два вопроса:
1.
Можно ли расширить систему аксиом аксиоматического исчисления путем добавления к ней в качестве новой аксиомы какой-нибудь недоказуемой в этом исчислении формулы?
2.
Является ли всякая тождественно истинная формула алгебры высказываний доказуемой в исчислении высказываний?
Рассмотренное нами исчисление высказываний полно как в узком смысле, так и в широком.
4.Проблема независимости аксиом исчисления высказываний.
Для всякого аксиоматического исчисления возникает вопрос о независимости его аксиом. Вопрос этот ставится так : можно ли какую-нибудь аксиому вывести из остальных аксиом, применяя правила вывода данной системы?
Если для некоторой аксиомы системы это возможно, то эту аксиому можно исключить из списка аксиом системы, и логическое исчисление при этом не изменится, т. е. класс доказуемых формул останется без изменений.
Определение 3.
23

Аксиома А называется независимой от всех остальных аксиом исчисления, если она не может быть выведена из остальных аксиом. Система аксиом исчисления называется независимой, если каждая аксиома системы независима.
Рассмотренная нами система аксиом исчисления высказываний независима.
Вопрос 20. 1.Логика предикатов. 2.Одноместные, двухместные и многоместные предикаты.
1. Понятие ``предикат'' обобщает понятие ``высказывание''. Неформально говоря, предикат – это высказывание, в которое можно подставлять аргументы. Если аргумент один – то предикат выражает свойство аргумента, если больше – то отношение между аргументами.
Пример предикатов. Возьмѐм высказывания: ``Сократ - человек'', ``Платон - человек''. Оба эти высказывания выражают свойство ``быть человеком''. Таким образом, мы можем рассматривать предикат ``быть человеком'' и говорить, что он выполняется для Сократа и Платона.
Возьмѐм высказывание: ``расстояние от Иркутска до Москвы 5 тысяч километров''. Вместо него мы можем записать предикат ``расстояние'' (означающий, что первый и второй аргумент этого предиката находятся на расстоянии, равном третьему аргументу) для аргументов ``Иркутск'', ``Москва'' и ``5 тысяч километров''.
Язык логики высказываний не вполне подходит для выражения логических рассуждений, проводимых людьми, более удобен для этого язык логики предикатов.
Пример рассуждения, не выразимого в логике высказываний. Все люди смертны. Сократ - человек.
Следовательно, Сократ смертен.
Это рассуждение на языке логики высказываний можно записать тремя отдельными высказываниями. Однако никакой связи между ними установить не удастся. На языке логики предикатов эти предложения можно выразить с помощью двух предикатов: ``быть человеком'' и ``быть смертным''. Первое предложение устанавливает связь между этими предикатами.
2. Одноместным предикатом р(х) на множестве М называется функция вида
Двуместным предикатом p(x1,x2) на множестве М называется функция вида
Знаки свойств называются одноместными предикатами. Знаками отношений являются многоместные предикаты. Так, предикаты Р(а) и Р(х) – одноместные. Предикаты R(х,у) и R(a,b,c) – многоместные: R(х,у) – двухместный предикат; R(a,b,c) – трехместный. Часто местность предиката указывают верхним индексом: R2(х,у), R3(a,b,c).
Пример 7. Высказывание «Всякий студент знает какой-нибудь иностранный язык» может быть записано на языке классической логики предикатов в следующем виде:
"х$yR(x,y),
где х употребляется вместо «студент», у - вместо «иностранный язык», R является знаком отношения «знает».
Классы студентов и иностранных языков называются областями значений соответственно х и у.
Информацию, заключенную в исходном высказывании, можно выразить более подробно:
"x(P(x) É $y(Q(y) Ù R(x,y))),
где P и Q обозначают теперь соответственно «студент» и «иностранный язык», рассматриваемые как знаки свойств (т.е. одноместные предикаторы), а х и у имеют единую область значений – множество «объектов вообще».
Пример 8. Высказывание «Если какое-то тело вторгается в атмосферу Земли, то оно вспыхивает» на языке логики предикатов запишется так:
24
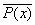
"x(P(x,a)ÉQ(x)),
где Р – отношение «вторгается»; Q – «вспыхивает»; а – «атмосфера Земли»; х – «тело».
Вопрос 21. 1.Логические операции над предикатами. 2.Кванторные операции. |
|
1. Отрицанием предиката Р(х), заданного на множестве Х, называется предикат |
, заданный на том же |
множестве и истинный при тех и только тех значениях х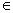 Х, при которых предикат Р(х) принимает значение лжи.
Х, при которых предикат Р(х) принимает значение лжи.
.Конъюнкцией предикатов Р(х) и Q(x), заданных на множестве Х, называется предикат Р(х)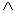 Q(x), заданный на том
Q(x), заданный на том
же множестве и обращающийся в истинное высказывание при тех и только тех значениях х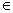 Х, при которых оба предиката принимают значения истины.
Х, при которых оба предиката принимают значения истины.
Если обозначить ТР – множество истинности предиката Р(х), ТQ – множество истинности предиката Q(х), а множество истинности их конъюнкции TPÙQ, то, по всей видимости, TPÙQ = TP Ç TQ.
Дизъюнкцией предикатов Р(х) и Q(x) называется предикат Р(х)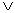 Q(x), определенный на том же множестве Х и обращающийся в истинное высказывание при тех и только тех значениях х
Q(x), определенный на том же множестве Х и обращающийся в истинное высказывание при тех и только тех значениях х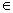 Х, при которых принимает значение истины хотя бы один из предикатов Р(х) или Q(x).
Х, при которых принимает значение истины хотя бы один из предикатов Р(х) или Q(x).
.Импликацией предикатов Р(х) и Q(x), заданных на множестве Х, называется предикат Р(х)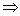 Q(x), определенный на
Q(x), определенный на
том же множестве Х и обращающийся в ложное высказывание при тех и только тех значениях х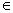 Х, при которых Р(х) принимает значение истины, а Q(x) – значение лжи.
Х, при которых Р(х) принимает значение истины, а Q(x) – значение лжи.
Эквиваленцией предикатов Р(х) и Q(x), заданных на множестве Х, называется предикат Р(х)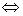 Q(x), определенный на том же множестве Х и принимающий значение истины при тех и только тех значениях х
Q(x), определенный на том же множестве Х и принимающий значение истины при тех и только тех значениях х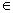 Х, при которых значения каждого из предикатов либо истинны либо ложны. Множество истинности в таком случае выглядит так: TPÛQ =
Х, при которых значения каждого из предикатов либо истинны либо ложны. Множество истинности в таком случае выглядит так: TPÛQ =
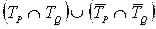 .
.
2.«для всех х» (для любого х, для каждого х) называется квантором общности и обозначается 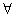 х.
х.
Высказывание «существует х» (для некоторых х, хотя бы для одного х, найдется такое х) называется квантором существования и обозначается 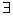 х.
х.
Высказывание «существует одно и только одно х» (для единственного значения х) называется квантором единственности : 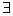 ! х.
! х.
Например: «Все кустарники являются растениями». Это высказывание содержит квантор общности («все»). Высказывание «существуют числа, кратные 5» содержит квантор существования («существуют»).
Для того чтобы получить высказывание из многоместного предиката, надо связать кванторами каждую переменную. Например, если Р(х; у) – двухместный предикат, то (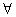 х
х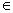 Х) (
Х) (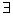 у
у Y) Р(х; у) – высказывание.
Y) Р(х; у) – высказывание.
Если не каждая переменная связывается квантором, то получается не высказывание, а предикат, зависящий от той переменой, которая не связана квантором. Так, если перед предикатом Р(х; у) поставить квантор 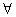 у, то получим предикат (
у, то получим предикат (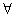 у
у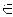 Y) Р(х; у), зависящий от переменной х.
Y) Р(х; у), зависящий от переменной х.
Вопрос 22. 1.Понятие формулы логики предикатов. 2.Основные равносильности логики предикатов.
1. ??????????
25
2. 1. 
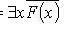 . 2.
. 2. 
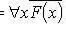 .
.
3. 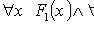
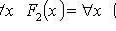
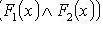 .
.
4. 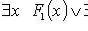
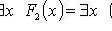
 .
.
5. 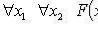
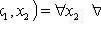
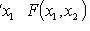 .
.
6. 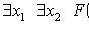
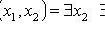
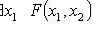 .
.
Вопрос 23. 1.Предваренная нормальная форма. 2.Общезначимость и выполнимость формул.
1. Для облегчения анализа сложных суждений формулы алгебры предикатов рекомендуется приводить к нормальной форме. Если в алгебре высказываний приняты две нормальные формы (ДНФ - дизъюнктивная и КНФ -конъюнктивная),
то в алгебре предикатов - одна предваренная нормальная форма (ПНФ), суть которой сводится к разделению формулы на две части: кванторную и безкванторную. Для этого все кванторы формулы выносят влево, используя законы и правила алгебры предикатов.
В результате этих алгебраических преобразований может быть получена формула вида: Âx1 Âx2 ¼Âxn(M), где ÂÎ{"; $}
, а М – матрица формулы. Кванторную часть формулы Âx1 Âx2 ¼Âxn иногда называют префиксом ПНФ.
В последующем матрицу формулы преобразуют к виду КНФ, что облегчает механизм по принципу резолюции.
Пример:
F=$x"y((P21.(х; y)ÚùP2.(х))&P3(y)) формула, приведенная к ПНФ; F="x(P21.(х; y)Ú$x(P2 (х))&$y(P3 (y)) формула,
неприведенная к ПНФ.
"x(P1.(х)) &"x(P2(x))="x(P1.(х) &P2(x)) слева от знака равенства формула, неприведенная к ПНФ, а справа,
равносильная ей формула, но приведенная к ПНФ.
2. Определение 1.
Формула А логики предикатов называется выполнимой в области М, если существуют значения переменных входящих в эту формулу и отнесенных к области М (иначе – существует модель), при которых формула А принимает истинные значения.
Определение 2.
Формула А логики предикатов называется выполнимой, если существует область, на которой эта формула выполнима.
Определение 3.
Формула А логики предикатов называется тождественно-истинной в области М (выполнимой), если она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.
Определение 4.
Формула А логики предикатов называется общезначимой, если она тождественна истинна на всякой области (на любой модели).
26
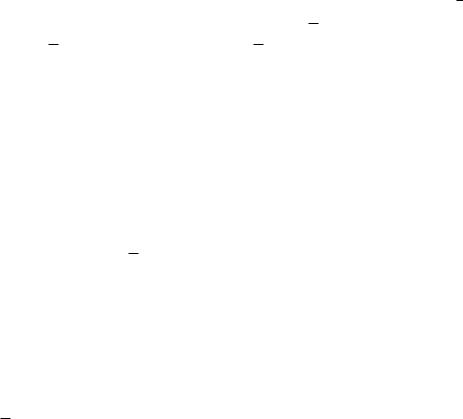
Если две равносильные формулы логики предикатов соединить знаком эквиваленции , то полученная формула будет принимать значение И для любого набора переменных в любой области, т.е. будет общезначимой.
Это понятие является обобщением понятия тождественной истинности формулы логики высказываний. Все логические законы, представленный в логике высказываний формулами (1 -30) являются общезначимыми формулами логики предикатов и выражают, как и другие общезначимые формулы, законы логики на языке логике предикатов.
Наиболее употребительные специфические законы логики предикатов, как было отмечено выше, представлены формулами (31 -54).
Общезначимость формулы логики предикатов, например, F обозначается ├F. Все общезначимые формулы могут быть источниками новых ├ формул. Например, подставляя в (14) – закон исключенного третьего x x – вместо х предикат Р(х1,…,хn), получаем общезначимую формулу Р(х1,…,хn) P (х1,…,хn). При n=1 имеем общезначимую формулу P(x) P(x) , и, таким образом , x[P(x) P(x)] - общезначимая формула логики предикатов.
Из тождественно истинной формулы логики высказываний (2) x y y x подстановкой вместо х предиката Р(х, y), а вместо y- предиката Q(x,y) получаем общезначимую формулу P(x, y) Q(x, y) Q(x, y) P(x, y) и т. д.
Определение 5.
Формула А логики предикатов называется тождественно ложной в области М, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области (иными словами, на данной модели).
Определение 6.
Формула А логики предикатов называется тождественно ложной (невыполнимой), если она тождественно ложна на всякой области (на всякой модели).
Например, формула x[P(x) P(x)] является тождественно ложной (невыполнимой) формулой логики предикатов.
Из приведенных определений с очевидностью следует:
1.Если формула А общезначима, то она и выполнима на всякой области (модели).
2.Если формула А тождественно истинна в области М, то она и выполнима в этой области .
3.Если формула А тождественно ложна в области М , то она не выполнима в этой области .
4.Если формула А не выполнима, то она тождественно ложна на всякой области (на всякой модели).
5.Для того, чтобы формула А логики предикатов была общезначима, необходимо и достаточно, чтобы ее отрицание было не выполнимо.
6.Для того, чтобы формула А логики предикатов была выполнимой, необходимо и достаточно, чтобы
формула A была не общезначима.
Вопрос 24. Проблема разрешимости в логике предикатов
Проблема разрешимости в логике предикатов ставится так же, как и в алгебре логики: существуют ли алгоритмы,
позволяющие для любой формулы А логики предикатов установить, к какому классу она относится, то есть является ли она или общезначимой, или выполнимой, тождественно ложной. Если бы такой алгоритм существовал то, как и в алгебре высказываний, он сводился бы к критерию тождественной истинности любой формулы логики предикатов.
Отметим, что в отличие от алгебры логики, в логике предикатов не применим метод перебора всех вариантов значений переменных, входящих в формулу, так как таких вариантов может быть бесконечное множество. В 1936
году американский математик А.Черч доказал, что проблема разрешимости логики предикатов в общем, виде алгоритмически не разрешима, то есть не существует алгоритма, который бы позволил установить, какому классу формул относится любая формула логики предикатов.
Вопрос 25. Запись математических предложений в виде формул логики предикатов.
27
Язык логики предикатов удобен для записи математических предложений. Он дает возможность выражать логические связи между понятиями, записывать определения, теоремы, доказательства. Приведем ряд примеров таких записей.
1. Определение предела числовой последовательности.
а = lim аn ↔ 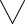 ε >
ε >  n0
n0 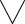 n є N(n≥n0→|an-a|< ε)
n є N(n≥n0→|an-a|< ε)
Здесь использован трехместный предикат Q(ε, n, n0): (n≥n0→|an-a|< ε)
2.Определение предела функции в точке.
b= lim F(x) ↔ 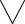 ε > 0
ε > 0  δ >0
δ >0  x є E(0<|x-x0|<δ→|f(x) - b|< ε)
x є E(0<|x-x0|<δ→|f(x) - b|< ε)
Здесь использован трехместный предикат P(ε, δ, x): (0<|x-x0|<δ→|f(x) - b|< ε)
3. Определение непрерывности функции в точке.
Функция f(х), определенная на множестве Е, непрерывна в точке x0 є E если
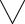 ε > 0
ε > 0 δ > 0
δ > 0 х є Е(|x-x0|<δ→<|f(x)- f(x0)|<ε).
х є Е(|x-x0|<δ→<|f(x)- f(x0)|<ε).
Здесь также использован трехместный предикат Р(ε, δ, x). 2. Определение возрастающей функции.
Функция f(x), определенная на множестве Е, возрастает на этом множестве, если
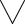 х є
х є 
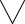 х2 є Е (х1 < х2 →f(x1)<f(x2)).
х2 є Е (х1 < х2 →f(x1)<f(x2)).
Здесь использован двуместный предикат W(x1 , x2):
(х1 < х2 →f(x1)<f(x2))
3. Определение ограниченной функции.
Функция f(x) определенная на множестве Е, если
 М є R+
М є R+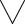 x є E (|f(x)| ≤ M).
x є E (|f(x)| ≤ M).
Здесь использован двухместный предикат L(x, M): (|f(x)| ≤ M).
Как известно, многие теоремы математики допускают формулировку в вида условных предложений. Например,
рассмотрим следующую теорему: «Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла».
Условием этой теоремы является предложение «Точка лежит на биссектрисе угла», а «включением — предложение
«Точка равноудалена от сторон угла». Видим, что и условие, и заключение теоремы представляют собой предикаты, заданные на множестве R2. Обозначая эти предикаты соответственно через Р(х) и Q(x), где х є R2 , теорему можем записать в виде формулы:
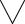 x є R2 (P(x)→Q(x)).
x є R2 (P(x)→Q(x)).
В связи с этим, говоря о строении теоремы, можно выделить в ней три части: 1) условие теоремы: предикат Р(х),
заданный на множестве R2;
2)заключение теоремы: предикат Q(x), заданный на множестве R2;
3)разъяснительная часть: в ней описывается множество объектов, о которых идет речь в теореме.
Вопрос 26. Построение противоположных утверждений.
Пусть дано некоторое математическое утверждение А. Ему будет противоположным будет утверждение 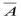 .
.
Логика предикатов позволяет путем равносильных преобразований формулы 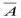 придать ей хорошо обозримый вид.
придать ей хорошо обозримый вид.
Определение неограниченной функции мы получим, беря отрицание этой формулы и проводя равносильные преобразования:
28

Последняя формула дает не негативное, а положительное определение неограниченной функции.
Из приведенного определения видно, что для построения противоположного утверждения к утверждению, заданному формулой логики предикатов, содержащей все кванторы впереди, необходимо заменить все кванторы на противоположные и взять отрицание от предиката, стоящего под знаком кванторов.
Особый интерес представляет построение утверждения, отрицающего справедливость некоторой теоремы: 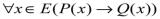 . Это будет утверждение:
. Это будет утверждение:
.
Вопрос 28. Доказательство методом от противного.
Доказательство методом от противного обычно проводится по следующей схеме: предполагается, что теорема
x є E(P(x) → Q(x)) |
(1) |
не верна, то есть существует такой объект х, что условие Р(х) истинно, а заключение Q(x) - ложно. Если из этих
предположений путем логических рассуждений приходят к противоречивому утверждению, то делают вывод о том, что
исходное |
предположение |
|
|
не |
верно, |
и |
верна |
|
теорема |
(1). |
||
Покажем, что такой подход дает доказательство истинности теоремы (1). Действительно, |
предположение о |
том, что |
||||||||||
теорема (1) не справедлива, означает истинность формулы |
|
|
|
|
|
|||||||
|
|
x є E(P(x) → Q(x)). Противоречивое утверждение, которое получается из допущенного предположения, есть |
||||||||||
|
|
|||||||||||
конъюнкция |
|
|
|
|
|
|
|
|
|
С&С, |
||
где |
С |
- |
некоторое |
высказывание. |
Таким |
|
образом, |
схема |
||||
доказательства |
от |
|
|
противного |
|
сводится |
|
к |
доказательству |
|||
истинности формулы |
; |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
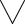 x є E(P(x) → Q(x))→С&С .
x є E(P(x) → Q(x))→С&С .
Легко видеть, что эта формула равносильна формуле (1).
Действительно,
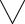 x є E(P(x) → Q(x))→С&С≡
x є E(P(x) → Q(x))→С&С≡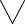 x є E(P(x) → Q(x)) v С&С≡
x є E(P(x) → Q(x)) v С&С≡
≡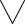 x є E(P(x) → Q(x)).
x є E(P(x) → Q(x)).
Вопрос 29. Замечания об аксиоматическом исчислении предикатов.
Аналогично тому, как была построена аксиоматическая теория высказываний, может быть построена и
аксиоматическая теория предикатов. При этом необходимо отметить следующее:
1.Определение формулы исчисления предикатов совпадает с определением формулы логики предикатов,
которое вводилось нами ранее. |
|
|
|
|
|
2. |
Выбор |
системы |
аксиом |
исчисления |
предикатов, |
как и в случае исчисления высказываний, может осуществляться по-разному. Одной из таких систем аксиом
может |
быть |
система, |
в |
которую |
включены |
одиннадцать |
аксиом |
|
исчисления |
высказываний, |
|
использованные |
нами, |
и две дополнительные аксиомы: |
|
|
|
|
||
29

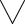 x (F(x)→F(y));
x (F(x)→F(y));
F(t)→ x F(x),
x F(x),
где t не содержит переменной х.
3. К правилам вывода, которые использовались в исчислении высказываний, добавляются еще два правила а) Правило введения квантора общности
F →G(x)
F → 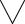 x G(x)
x G(x)
б) Правило введения квантора существования
G(x) → F
 xG(x)→F ,
xG(x)→F ,
если F не зависит от х.
4.Понятие вывода и доказуемой формулы определяются аналогично этим понятиям в исчислении высказываний.
5.Как и во всякой аксиоматической теории, рассматриваются проблемы:
а) разрешимости,
б) непротиворечивости,
в) полноты,
г) независимости.
Вопрос 30. Понятие алгоритма и его характерные черты.
Понятие алгоритма принадлежит к числу основных понятий математики. Примерами алгоритмов являются:
1.Правила выполнения арифметических действий над числами.
2.Правило отыскания наибольшего общего делителя (алгоритм Евклида).
3.Правило извлечения квадратного корня.
4.Правило отыскания решений квадратного уравнения.
5.Правило отыскания производной многочлена n-ой степени.
6.Правило интегрирования рациональной функции.
Вкаждом из приведѐнных примеров приходится иметь дело с классом однотипных задач, или, как говорят, с
массовой проблемой. Задачи такого класса отличаются друг от друга значениями входящих в них параметров. Так, в задаче отыскания решения квадратного уравнения ax2+bx+c=0 участвует три параметра a, b и c; меняя их, получаем различные задачи одного класса.
Всвязи со сказанным можно дать следующее интуитивное определения понятия алгоритма.
Алгоритмом называется общий единообразный, точно определѐнный способ решения любой задачи из данной массовой проблемы.
Отметим характерные черты понятия алгоритма.
1.Дискретность алгоритма. Алгоритм – это процесс последовательного построения величин таким образом, что в начальный момент задаѐтся исходная конечная система величин, а в каждый следующий момент система величин получается по определѐнному закону из системы величин, имевшихся в предыдущий момент.
2.Детерминированность алгоритма. Система величин, получаемых в какой-то не начальный момент, однозначно определяется системой величин, полученных в предшествующие моменты времени.
3.Элементарность шагов алгоритма. Закон получения последующей системы величин из предшествующей должен быть простым.
4.Массовость алгоритма. Начальная система величин может выбираться из некоторого потенциально бесконечного множества.
5.Результативность алгоритма. Последовательный процесс построения величин должен быть конечным и давать результат, то есть решение задачи.
30
