биофизика

Решение:

Здесь удобно использовать формулу (7.9), перейдя к противоположному событию "среди пяти отобранных костей домино нет ни одной шестерки".

Число всех исходов

	n = C215 =	28 27 26 25 24	= 98280 .
		1 2 3 4 5

Т.к. количество костей домино, не содержащих шестерку, равно 21, то число исходов, благоприятствующих противоположному событию, будет:

				m = C215 =		21 20 19 18 17	= 20349 .
		m				1 2 3 4 5
				20349
	Отсюда q =		=		= 0,207 и p =1 − q = 0,793 .
		n		98280

14. Из пяти карточек с буквами А, Б, В, Г, Д наугад выбираются три и располагаются в ряд в порядке появления. какова вероятность того, что получится слово "два".

Решение:

Так как положение буквы в комбинации имеет значение, то для определения общего числа возможных исходов следует пользоваться размещениями:

n = A53 = 5 4 3 = 60 .

Здесь m =1. т.к. требуется получить только одно слово "два". Следовательно p = 601 .

7.1.3. Относительная частота и статистическая вероятность случайного события.

Один из возможных подходов к понятию вероятности связан с явлением, которое называется устойчивостью частоты случайного события. Будем повторять данное испытание большое число раз, всякий раз наблюдая, происходит ли интересующее нас событие А. Если мы обнаружим, что в первых n испытаниях событие А произошло m раз, то отношение m/n будет называться относительной частотой или просто частотой события А для данной серии n испытаний. Если относительную частоту события А

242

обозначать через W(А), то по определению имеем W(А)= m/n. При наблюдениях относительной частоты для возрастающих значений n обнаруживается, что эта частота имеет тенденцию к стабилизации. Другими словами, частота колеблется около некоторого постоянного ее значения, и колебания эти уменьшаются при условии возрастания n. Если n - малое число, то при изменении n частота W(A) претерпевает значительные колебания. Но чем больше n, тем меньше становятся колебания частоты. Это явление и называется устойчивостью относительной частоты случайного события. Оно подтверждается многочисленными экспериментами.

Под вероятностью события А понимается постоянное число р, около которого колеблется относительная частота наступления события А при многократных испытаниях. Утверждение, что случайное событие А имеет вероятность р, обычно записывают так:

Р(А)=р.

Утверждение о существовании у события А определенной вероятности заключается, таким образом, в том, что в различных достаточно больших сериях испытаний получаемые частоты W(А) будут примерно одинаковы и близки к р.

При достаточно большом числе испытаний будем иметь приближенное равенство р=Р(А)≈W(А)= m/n. Из представления о вероятности как о числе, около которого колеблется частота W(А) случайного события А, которая, очевидно, всегда удовлетворяет равенству 0≤ W(А)≤1, вытекает, что вероятность Р(А) любого события А естественно считать лежащей между нулем и единицей.

0≤ Р(А)≤1

Так, при бросании симметричной монеты вероятность выпадения герба на основании классического определения будет, очевидно, равна 0,5. Английский статистик К. Пирсон (1857 - 1936)

243

бросил монету 24000 раз, при этом герб выпал 12012 раз, следовательно относительная частота выпадения герба оказалась равной 0,5005, т.е. примерно равна вероятности 0,5.

7.1.4. Правила сложения и умножения вероятностей .

Как уже говорилось, произведением АВ называется событие, которое происходит тогда и только тогда, когда происходит и А и В. Событие В называется зависимым от события А, если вероятность появления события В зависит от того, имело место событие А или нет. В этом случае вероятность события В называется условной и обозначается P(B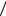 A) .

Сформулируем теперь правило умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого при

наступлении первого, т.е.
Р(А В) = Р(А) Р(В/А)	(7.10)
или
Р(А В) = Р(В) Р(А/В)	(7.11)

Если события А и В независимы, то вероятность их произведения равна произведению их безусловных вероятностей:

Р(А В)=Р(А) Р(В). (7.12)

Суммой двух событий называется событие, которое состоит в том, что произошло по крайней мере одно из событий А или В. События называются несовместными, если появление при испытании одного из них полностью исключает появление других. Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий, т.е.

244

Р(А+В)=Р(А)+Р(В) (7.13)

Если событие A является отрицанием события А, то события A и А называются противоположными.

Сумма вероятностей противоположных событий равна единице:

P(A) + P(

A

) =1.

(7.14)

Последняя формула очень важна в практическом отношении, так как позволяет вычислить вероятность события А, если известна вероятность противоположного события A . Если события Е1, Е2,...Еn несовместны, то

	n		n	(7.15)
P	∑Ei		= ∑P(Ei )
i=1			i=1

Пример 1. Определить вероятность того, что партия из 15 изделий, среди которых 5 бракованных, будет принята после выборочного контроля 4 вместе взятых изделий. Условием приемки является обнаружение не более одного бракованного изделия среди 4-х проверяемых.

Решение:

Введем обозначения:

А - событие, состоящее в том, что партия изделий принята; В - все четыре проверяемые изделия качественные; С - среди четырех проверяемых одно изделие бракованное. Очевидно, что А=В+С,

	P(B) =	C104	=		2	;	P(C) = 5	C103	=	40	;	P(A) = P(B) + P(C) =		2	+	40	=	54	.
		C154		13				C154		91			13			91		91

Пример 2. В клетке находится 10 мышей, причем 4 из них серые. Наугад берут трех мышей. Найти вероятность того, что хотя бы одна мышь серая.

Решение:

Обозначим события:

245

А – одна мышь серая, две – нет ; В – две серые, одна – нет ; С – все серые ;

D – ни одной серой.

P(A + B + C) = P(A) + P(B) + P(C) =

C41 C62

+

C42 C61

+

C43

=

5

;

C103

C103

C103

6

или

P =1 − P(D) =1 −

C63

=

5

.

C103

6

Пример 3. Некоторая вакцина

эффективна

на

75% в

формировании иммунитета. Вакцинировали 2 человек. Пусть А и В

– события, состоящие в том. что соответственно первый и второй человек приобретает иммунитет. Найти вероятность того, что:

а) оба человека приобрели иммунитет; б) первый приобрел иммунитет, а второй нет; в) оба не приобрели иммунитета.

Решение:

а) P(AB) = P(A) P(B) = 0,75 0,75 = (0,75)2 ;

б) P(AB) = P( A) (1 − P(B)) = 0,75 0,25 ;

в) P( AB) = (1 − P(A)) (1 − P(B)) = 0,25 0,25 = (0,25)2 .

Пример 4. Студент извлекает по одному билету из 34 экзаменационных. Какова вероятность того, что он сдаст экзамен, если подготовлено 30 билетов, и первый вытянутый билет студент не знал?

Решение:

Обозначим события:

А – первый билет неудачный; В – второй билет удачный.

246

P(A B) = p(A) p(B A) = 344 3033 = 18720 .

Если появление одного события не исключает появление других, то такие события называются совместными. Другими словами, вероятность суммы двух совместных событий равна сумме их вероятностей минус вероятность совместного их появления в данном испытании, т.е.

P( A + B) = P( A) + P(B) − P( A B)

(7.16)

Пример 5. В марте 7 дней шел снег, 10 – дождь, 4 дня – снег с дождем. Найти вероятность того, что в наугад выбранный день шел дождь или снег.

Решение:

P(A + B) = P(A) + P(B) − P(AB) = 317 +1031 − 314 = 1331.

Пример 6. Из 100 студентов, находящихся в аудитории, 50 человек знают английский язык, 40 – французский, 35 – немецкий. Английский и французский знают 20 человек, английский и немецкий – 8, французский и немецкий – 10. Все три языка знают 5 человек. Один из студентов вышел. Определить вероятности следующих событий:

1.Вышедший студент знает английский и французский языки.

Решение:

Обозначим события: А – знает английский; В – знает французский.

P(D) = P(A + B) = P( A) + P(B) − P( AB) = 0,5 +0,4 −0,2 = 0,7.

2. Знает английский или немецкий языки.

247

Решение:

Событие:

С – знает немецкий.

P(D) = P(A +C) = P(A) + P(C) − P(AC) = 0,35 +0,5 −0,08 = 0,77.

3. Знает немецкий или французский языки.

Решение:

P(D) = P(C + B) = P(C) + P(B) − P(CB) = 0,35 +0,4 −0,1 = 0,65.

4.Кроме английского языка знает или французский, или немецкий.

Решение:

P(D) = P(AB + AC) = P(AB) + P(AC) − P(ABC) = 0,2 +0,08 −0,05 = 0,23.

7.1.5. Формула полной вероятности.

Из правил сложения и умножения вероятностей можно вывести полезные для практики формулы. Одной из них является так называемая формула полной вероятности. Имеет место следующая теорема.

Теорема. Пусть Н1, Н2,...,Нn - полная группа попарно несовместых событий (гипотез), причем событие А может произойти только вместе с одной из этих гипотез. Тогда для вероятности Р(А) появление события А имеем :

n	(7.17)
P(A) = ∑P(Hi ) P(A Hi ) ,

i=1

т.е. вероятность события А равна сумме произведений вероятностей каждой гипотезы на соответствующие условные вероятности события А.

Пример 1. Вероятность брака при изготовлении детали равна 0,04. Приемка деталей производится по следующей системе

248

контроля: годная деталь принимается с вероятностью 0,98, а бракованная с вероятностью 0,1. Найти вероятность приемки детали.

Решение:

Пусть А – событие "деталь принята", Н1 – (гипотеза) изготовлена хорошая деталь, Н2 – изготовлена бракованная деталь.

Из условия найдем вероятности гипотез и условные вероятности: p(H1 ) = 0,96, p(H2 ) = 0,04 .

p(AH1 ) = 0,98 - вероятность того, что принятая деталь хорошая, p(AH2 ) = 0,1- вероятность того, что принятая деталь бракованная.

Полная вероятность того, что деталь будет принята, на основании формулы (7.17) равна

P(A) = p(H1 ) p(A H1 ) + p(H2 ) p(A H2 ) = 0,96 0,98 + 0,04 0,1 = 0,9448

Пример 2. Имеются три одинаковых ящика с шарами. В первом ящике 30 белых и 20 черных шаров, во втором – 15 белых и 15 черных шаров, в третьем – 5 белых и 15 черных шаров. Какова вероятность вытащить из случайно выбранного ящика черный шар.

Решение:

Обозначим гипотезы:

Н1 – выбран первый ящик, Н2 – выбран второй ящик, Н3 – выбран третий ящик.

Т.к. выбор того или иного ящика – события равновероятные, то:

p(H1 ) = p(H 2 ) = p(H3 ) = 13 .

p(A H1 ) = 5020 = 52 - вероятность того, что черный шар вытащили из первого ящика,

249

p(A H 2 ) = 1530 = 12 - вероятность того, что черный шар вытащили из второго ящика.

p(A H3 ) = 1520 = 34 - вероятность того, что черный шар вытащили из

третьего ящика.

По формуле (7.17) найдем искомую вероятность

P(A) = p(H1 ) p(A H1 ) + p(H 2 ) p(A H 2 ) + p(H3 ) p(A H3 ) =	1		2	+	1		1	+	1		3	=
= 0,55.	3		5		3		2		3		4

7.1.6. Формула Байеса.

Пусть имеется полная группа несовместимых гипотез H1, H2,....., Hn и пусть в результате произведенного испытания появилось некоторое событие А.

Впрактических приложениях часто требуется высказать суждение

отом, какая из гипотез Hi (i=1, n ) имеет место. Решить этот вопрос с полной определенностью невозможно. Поэтому ставится такая задача: какую вероятность нужно приписать каждой из гипотез Hi

(i=1, n ), если известно, что произошло событие А. При этом предполагается, что известны априорные (доопытные) вероятности Р(Hi) всех гипотез и условные вероятности P(А/Hi) события А при наличии гипотез Hi (i=1, n ).

Таким образом, поставленная задача сводится к переоценке вероятностей гипотез в связи с наличием нового фактора - наступления события А. Решение задачи дается следующей теоремой.

Теорема. Условная вероятность гипотезы Hi (i=1, n ) вычисленная в предположении, что некоторое событие А наступило, определяется по формуле:

250

P(Hi / A) =	P(Hi ) P(A / Hi )	,	(7.18)
	n
	∑P(Hi ) P(A / Hi )

i=1

называемой формулой вероятностей гипотез или формулой Байеса. Пример 1. В группе 10 студентов, пришедших на экзамен. Трое подготовлены отлично, 4 – хорошо, 2 – посредственно, 1 – плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный – на 16, посредственно – на 10, плохо подготовленный – на 5. Вызванный наугад студент ответил на 3 заданных вопроса. Найти вероятность того, что этот студент

подготовлен:

1)отлично,

2)плохо.

Решение:

Из условия задачи вытекают следующие гипотезы: Н1 – подготовлен отлично; Н2 – подготовлен хорошо;

Н3 – подготовлен посредственно; Н4 – подготовлен плохо. Вероятности этих гипотез равны:

P(H1 ) = 0,3; P(H 2 ) = 0,4; P(H3 ) = 0,2; P(H 4 ) = 0,1;

Найдем соответствующие условные вероятности:

	P(A / H1 ) =1;
	P(A / H 2 ) =	16			15			14	= 0,491;
		20		19			18
	P(A / H3 ) =	10			9			8	= 0,105;
		20		10			18
	P(A / H 4 ) =	5			4			3	= 0,009.
		20		19			18

полная вероятность

251