биофизика

Случайная величина называется величиной дискретного типа или просто дискретной, если она может принимать конечное или счетное множество значений.

Случайная величина называется величиной непрерывного типа, если она может принимать любые значения в одном или нескольких заданных интервалах.

7.2.1. Закон распределения вероятностей дискретной случайной величины.

Рассмотрим дискретную случайную величину X c конечным множеством значений x1, x2, ..., xn. Закон распределения этой случайной величины будет задан, если известны все вероятности

P(X = xi) = pi (i=1, n ).

Совокупность всех значений xi случайной величины X и вероятностей pi называется рядом распределения величины X, который может быть задан с помощью таблицы следующего вида:

X	x1		x2		.....................	xn
P(X = xi)	p1		p2		.....................	pn
Очевидно, что		всегда должно			быть выполнено условие

∑pi =1, так как события {X=xi} (i=1, n ) несовместимы и образуют полную группу.

Важный пример дискретной случайной величины дает число m появлений некоторого события в серии последовательных испытаний, проведенных по схеме Бернулли. Обозначим через X число появлений события А в n испытаниях. При этом его ряд распределения задается формулой Бернулли:

P(X=m) = Cnm pm qn-m; m = 0, 1, 2,....., n; q = 1 – p.

262

Если ряд распределения случайной величины X задается формулой Бернулли, то закон распределения вероятностей величины называется биномиальным.

Закон распределения дискретной случайной величины можно задавать по-другому, а именно с помощью так называемого интегрального закона распределения или функции распределения вероятностей. Функцией распределения F(x) случайной величины X называется вероятность того, что величина X примет значение,

меньшее чем x: F(x)=P(X<x), где x – произвольное вещественное число.

Заметим сразу же, что функция распределения вероятностей F(x) случайной величины Х является универсальной характеристикой Х, она существует для случайной величины любого типа.

	Очевидно, что если Х – дискретная случайная величина, то ее
функция распределения определяется посредством равенства
	F(x) = ∑ pi	(7.21)
	xi <x
	Пример 1. Построить функцию распределения дискретной
случайной величины Х, если известен ее ряд распределения:
Х	0	1	2
Р	0,3	0,2	0,5

Решение . Если х ≤ 0, то F(x) ≡ 0, поскольку в данном случае событие Х<х является невозможным.

Если 0 < х ≤ 1, то событие Х<х равносильно событию Х = 0. Поэтому для данного промежутка F(x) = P(X = 0) = 0,3.

Аналогично, если 1< х ≤ 2, то F(x) = P(X = 0) + P(X = 1) = 0,5.

Наконец, если х>2, то F(x)≡1, поскольку теперь событие Х<х становиться достоверным. Итак функция распределения такова:

263

0, еслихх≤0

0,3, если0 < x ≤1

F(x) =

0,5, если1 < x ≤ 2

1, еслихх> 2

График данной функции распределения имеет вид:

График F(x) дискретной случайной величины и в общем случае оказывается ступенчатым со скачками в точках х1, х2, ...., хn равными соответственно р1, р2, ...., рn. Само распределение дискретной случайной величины также называется дискретным.

Пример 2. Построить ряд распределения случайной величины Х, представляющей собой число выпадения герба при двукратном

бросании монеты.
Решение:
	Х		0			1		2
	р			1		1		1
			4			2		4

			1		1		1		1			1			1			1		1		1
	p(X = 0)	=				=		;	p(X =1) = 2					=		;	p(X = 2) =				=		.
			2		2		4			2		2			2			2		2		4

Пример 3. Из партии в 25 изделий, среди которых имеются 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения случайного числа

F(x)
1
0,5
0,3
0	1	2	x
	Рис. 7.8. Функция распределения ДСВ

264

бракованных изделий, содержащихся в выборке. Решение:

			C 3
p(X = 0) =			19			≈ 0,42;
			C253
	6C 2
p(X =1) =	19					≈ 0,45;
			C253
		19C			2
p(X = 2) =				6			≈ 0,12;
			C253
			C 3
p(X = 3) =		6			≈ 0,01;
		C253
Х					0			1	2	3

р0,42 0,45 0,12 0,01

7.2.2.Функция распределения и плотность вероятности непрерывных случайных величин.

Пусть Х является случайной величиной непрерывного типа. Множество значений такой случайной величины несчетно, поэтому мы не можем выписать в последовательность и занумерованность все ее значения и, следовательно, не можем задать ее закон распределения рядом распределения. В этом случаи на помощь приходит функция распределения, с помощью которой можно характеризовать закон распределения случайной величины любого типа. Случайная величина Х (любого типа) считается заданной, если известна ее функция распределения, т. е. функция F(x) = P(X<x).

Рассмотрим некоторые основные свойства функции распределения F(x) произвольной случайной величины Х. Прежде всего, как всякая вероятность, F(x) удовлетворяет при любом х

265

неравенству 0≤F(x)≤1, так что график функции y = F(x) всегда лежит в полосе между прямыми y = 0, y = 1.

При помощи функции распределения F(x) можно всегда определить вероятность попадания случайной величины Х на промежуток [α, β) при любых значениях α и β.

В самом деле, если через А обозначить событие, состоящее в том, что X < β , через В - событие, состоящее в том, что Х<α, и ,

наконец, через С - событие α≤х<β, то очевидно, что А=В+С. Следовательно, по правилу сложения вероятностей для

несовместимых событий Р(А)=Р(В) + Р(С), откуда Р(С) = Р(А) –

Р(В). Но Р(А) = Р(Х<β) = F(β), P(B) = F(α).
Поэтому окончательно
Р(α≤Х<β) = F(β) – F(α),	(7.20)

т. е. вероятность попадания случайной величины в промежуток [α,

β) равна приращению функции распределения на этом промежутке.

Так как вероятность Р(α≤Х<β) неотрицательна, как всякая вероятность, то из последнего равенства следует, что F(β)≥F(α), если

β>α, т. е. функция распределения любой случайной величины является неубывающей функцией.

Если случайная величина Х является ограниченной, т. е. все ее возможные значения лежат на каком-либо конечном отрезке [а, в], мы будем иметь равенства

	0,	x ≤ a
	F(x) =	x > b
	1,
В общем случае, когда величина Х может быть и
неограниченной, будут иметь место следующие соотношения:
F(- ∞) = lim	F(x) = 0
x→−∞
F(+∞) = lim	F(x)=1
x→+∞

266

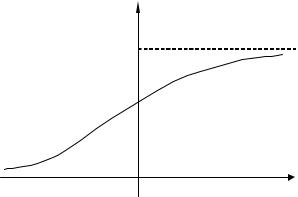
F(x)
1
0	x

Примером может служить функция распределения случайной величины, распределенной по показательному закону:

0, x ≤ 0

F(x) = 1	−e−λx ,	x > 0, λ > 0	(7.23)

Если случайная величина Х принадлежит к непрерывному типу, то для любого α имеем равенство:

Р(Х = α) = 0.

Напомним, что для дискретных случайных величин Р(Х = α)

отлично от нуля, если α совпадает с каким-либо частным значением этой случайной величины.

Таким образом, любая непрерывная случайная величина Х не может быть характеризована вероятностями своих значений, поскольку все эти вероятности равны нулю.

Чтобы преодолеть эту трудность, вводится понятие плотности вероятности.

Плотностью вероятности или дифференциальным законом распределения вероятностей случайной величины Х называется

Рис.7.9. Функция распределения НСВ.

функция f(x), определяемая равенством:

f(x) = lim P(x < X < x+∆x)/∆x

∆x→0

Рассмотрим свойства плотности вероятности.

267

Во-первых, очевидно, что f(x) ≥ 0, поскольку вероятность неотрицательна.

Во-вторых, числитель правой части последней формулы может быть заменен разностью F(x+∆x) – F(x).

На основании определения производной получим выражение плотности вероятности через функцию распределения:

f(x) = F′(x)

(7.24)

Третье свойство плотности вероятности может быть получено, если сопоставить равенство P(α<βΧ)=F(β)−F(α) для непрерывной случайной величины с формулой Ньютона-Лейбница

∫αβ f (x)dx = F(β) − F(α)	(7.25)
Это сопоставление позволяет	получить выражение для

вероятности попадания случайной величины Х непрерывного типа на интервал (α,β) через ее плотность вероятности f(x):

P(α < X < β) = ∫αβ f (x)dx

(7.26)

Заменяя в последнем равенстве β на х, устремляя α→−∞ и пользуясь определением функции распределения, получим четвертое свойство плотности вероятности, позволяющее найти функцию распределения, если известна плотность вероятности:

F(x) = ∫−x∞ f (x)dx	(7.27)
Последнее, пятое свойство получим, если верхний предел х
интеграла последней формулы устремим к + ∞:
∫−+∞∞ f (x)dx = 1.	(7.28)

Это означает, что площадь, ограниченная осью абсцисс и графиком плотности вероятности, равна 1.

268

Задача 1. Дана функция распределения непрерывной случайной величины Х:

		x ≤ 0
	0,				p
	F(x) = sin x, 0 < x ≤
					2
			p
		x >
	1,
			2

Найти плотность вероятности f(x) и построить ее график. Решение:

	x	≤ 0
0,					p
f (x) = F(x) = cos x,			0	< x ≤
					2
			p
	x	>
1,
			2

Задача 2. Дана плотность распределения случайной величины

Х:

0,	x ≤ 0
f (x) = a sin x, 0 < x ≤π
	x >π
0,

Определить коэффициент а и функцию распределения F(x), построить график функции F(x).

Решение:

f(x)

1

0

π/2

x

Рис. 7.10. Плотность распределения к примеру 2.

269

	∞	0	π		∞				1
	∫ f (x)dx = ∫dx +∫a sin xdx + ∫					0 dx =1 a =				.
									2
	−∞	−∞	0		π
			x
	x ≤ 0; F(x) = ∫0 dx = 0;
			−∞
			0	x	1		1				x
	0 < x ≤π;	F(x) = ∫0 dx +∫				sin xdx = −		cos x
					2		2
			−∞	0							0

= − 12 cos x + 12 = 12 (1 − cos x);

		0	π	1		x
	x >π; F (x) = ∫0 dx + ∫				sin x + ∫0 dx =1, т.е.
				2
		−∞	0			π
	x	0,	x ≤ 0
	F(x) = ∫		−cos x),			0 < x ≤π
		f (x)dx = a(1
	−∞		x >π
		1,

7.2.3. Числовые характеристики случайных величин.

Для полной характеристики распределения случайной величины Х необходимо знать, как мы видели, ее функцию распределения или, в случае непрерывной Х, ее плотность вероятности. Однако в ряде практических задач нет необходимости в таком полном исследовании случайной величины Х и бывает достаточно иметь хотя бы грубое представление о распределении Х, описать его посредством немногих простых параметров. В ряде случаев достаточно знать:

1)примерное расположение того интервала значений, в котором находится основная масса вероятности случайной величины Х, а так же положение «центра группирования» на числовой оси;

2)насколько широко разбросаны значения случайной величины Х по

каждую сторону от «центра группирования».

Параметры первого рода, характеризующие положение центра группирования, называются характеристиками расположения ( или положения); параметры второго рода, характеризующие разброс

270

значений случайной величины около центра группирования, называются характеристиками рассеивания.

Наиболее часто употребляемой характеристикой расположения является так называемое математическое ожидание случайной величины Х, которое будем обозначать символом М(Х).

Рассмотрим сначала математическое ожидание дискретной случайной величины Х, заданной таблицей распределения.

Математическое ожидание такой величины есть по определению сумма произведений всех ее возможных частных значений на соответствующие им вероятности:

n
M ( X ) = ∑ x i p i .		(7.29)
i =	1

Если возможные значения дискретной случайной величины Х составляют счетное множество и она задана рядом распределения Р(Х = хi) = рi, (i = 1, 2, 3, ...), то по определению математическое ожидание Х равно сумме ряда:

∞
M ( X ) = ∑ x i p i	(7.30)

i =1

Математическое ожидание непрерывной случайной величины определяется равенством

+∞
M (X ) = ∫xf (x)dx	(7.31)

−∞

В этом равенстве f(x) есть плотность вероятности.

Пример 1. Найти математическое ожидание случайной величины, принимающей только два значения: 1 и 0, с вероятностью р и q соответственно.

Решение:

По определению математического ожидания имеем:

М(Х) = 1 р + 0 q = р.

271