1.3.3. Энергия затухающих колебаний

Эта энергия складывается из потенциальной и кинетической

П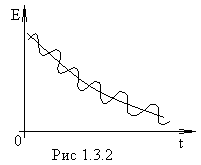осле подстановки сюда выражений,из (1.3.1) получим зависимость, которая графически представлена на рисунке 1.3.2.Уменьшение энергии колебаний обусловлено работой силы сопротивления.

Энергия системыпропорциональна квадрату амплитуды и при затухающих колебаниях убывает по закону

где -энергия колебаний в начальный момент времени(рис.1.3.2).

Продифференцировав это выражение по времени, получим скорость убывания энергии

Если изменение энергии за период мало, убыль энергииравна

тогда

- при слабом затухании добротность пропорциональна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний.

С ростом коэффициента затухания период увеличивается, и при период колебаний обращается в бесконечность, т.е. движение перестает быть гармоническим.

1.4. Вынужденные колебания

1. Уравнение вынужденных колебаний

Будучи предоставлена сама себе, любая колебательная система через некоторое время остановится вследствие трения. Чтобы колебания не затухали, необходимо периодическое воздействие внешней силы, изменяющейся - в простейшем и наиболее важном случае - по гармоническому закону . Такие колебания называются вынужденными.

Вынужденные колебания – колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы.

Теперь на колеблющуюся частицу будут действовать одновременно три силы:

• квазиупругая ,

• сила сопротивления , гдеr- коэффициент сопротивления

• внешняя вынуждающая сила F_x.

Если внешняя сила (вынуждающее действие) меняется по гармоническому закону, то вынужденные колебания будут гармоническими.

Согласно основному уравнению динамики .

Уравнение такого колебательного процесса

(1.4.1)

г_{де β – коэффициент затухания,}

_{– собственная частота системы,}

_{, где – амплитуда вынуждающей силы,}

_{– частота изменения силы.}

_{Общее решение этого неоднородного дифференциального уравнения:}

(1.4.2)

_{где и – произвольные постоянные.}

_{Получим частные решения уравнения (1.4.1), воспользовавшись методом векторных диаграмм.}

_{Пусть частное решение имеет вид:}

(1.4.3)

_тогда

_{Подставив в (1.4.1), получаем}

(1.4.4)

_{Из выражения (1.4.4) следует, что постоянные а и φ должны иметь такие значения, чтобы гармоническая функция была равна сумме трёх гармонических функций, стоящих в левой части уравнения.}

_{Если изобразить:}

_{- функцию вектором длины , направленным вправо,}

_{- то функция отобразится вектором длины , повёрнутым на π/2 против часовой стрелки,}

_{- а функция – вектором длины , повёрнутым относительно вектора a на π (рис.1.4.1)}

_{Сумма этих векторов(по теореме Пифагора) равна:}

_тогда

₍1.4.5₎

_{Из рисунка:}

_{- определяет отставание смещения по фазе на от вынуждающей силы.}

_{Формулы 1.4.5 показывают, что амплитуда колебаний и отставание смещения по фазе на от вынуждающей силы определяются свойствами самого осциллятора. и вынуждающей силы, но не начальными условиями.}

_{Подставив а и φ в (1.4.3), получим некоторое частное решение уравнения (1.4.1):}

(1.4.6)

_{Сумма общего (1.4.2) и частного (1.4.6) решений даёт решение уравнения (1.4.1), описывающего поведение системы при вынужденных колебаниях.}

_{Слагаемое (1.4.6) играет заметную роль только в начальной стадии процесса, при установлении колебаний. С течением времени из за экспоненциального множителя e}-βt _{слагаемое (1.4.2) всё больше уменьшается и далее им можно пренебречь. Функция (1.4.6) описывает установившие его вынужденные колебания с частотой, равной частоте вынуждающей силы (рис.1.4.2).}