5.8.Уравнение даламбера

При соблюдении условий ((5.18) последнее слагаемое в первом из уравнений (5.15) обращается в ноль. Кроме того, производная по времени от имеет значение

следовательно,

(5.22)

(5.23)

Таким образом, вместо двух взаимосвязанных уравнений мы получили два раздельных уравнения, причем уравнения для иφ приобрели сходную форму.

Дифференциальное уравнение вида

(5.24)

называется уравнением Даламбера. Его можно записать очень компактно, если ввести оператор Даламбера

ٱ

Тогда уравнение (5. 24) принимает вид ٱ f=

В стационарном случае производные по времени обращаются в ноль, и уравнение Даламбера переходит в уравнение Пуассона.

С использованием символа ٱ (Даламбера) уравнения (5.22) и (5.23) принимают вид

ٱٱ

Эти уравнения описывают электромагнитные поля проще, чем уравнения Максвелла, поэтому бывает легче вычислить потенциалы иφ, а потом по формуламвычислитьи.

Из уравнений Максвелла следует, что электромагнитное поле способно существовать в отсутствие электрических зарядов и токов. При этом уравнение его состояния обязательно носит волновой характер. Поле такого рода называют электромагнитными волнами.

Лекция 22

5.9.Энергия и импульс электромагнитного поля

СОХРАНЕНИЕ ЭНЕРГИИ И ИМПУЛЬСА В ИЗОЛИРОВАННОЙ СИСТЕМЕ ПРОИЗВОЛЬНО ДВИЖУЩИХСЯ ЗАРЯДОВ

Как всякий материальный объект, электромагнитное поле обладает импульсом, энергией и моментом импульса. Эти величины для поля сохраняются, если оно оказывается изолированным. Условие изолированности выполняется в тех случаях, когда в области существования поля нет электрических зарядов и токов. Такое поле называется свободным. Сохранение энергии, импульса и момента импульса изолированного поля является следствием однородности пространства и времени и изотропности пространства. При взаимодействии электромагнитного поля с зарядами и токами сохраняются суммарные величины для поля и заряженных частиц. Так, сохраняется полная сумма импульсов электромагнитного поля и заряженных частиц.

Поскольку поле всегда занимает некоторую область пространства, энергия, импульс и момент импульса всегда характеризуются их удельными значениями, т.е. соответствующей величиной, отнесенной к единице объема в данном месте пространства. Эти величины называются соответственно плотностью энергии w, импульса, и момента импульса. Каждая из этих функций зависит от времениtи радиус-вектораданной точки пространства.

Из уравнений Максвелла-Лоренца можно получить значения этих плотностей и законы их сохранения.

5.10. Работа, совершаемая полем при перемещении зарядов

Определения кинетической и потенциальной энергии, а также импульса и момента импульса, данные в механике для материальной точки и системы материальных точек, отнюдь не распространяются на поля.

Рассмотрим систему заряженных материальных точек, взаимодействующих между собой. Такая система описывается уравнениями Максвелла-Лоренца. Пользуясь этими уравнениями, распространим понятия энергии и импульса на поля, находя величины, сохраняющиеся для изолированной системы поле - заряды. Макроскопические электрические заряды, так или иначе, связаны с материальными телами, на которых они расположены. Пусть частица массой

несет заряд. Тогда по второму закону Ньютона уравнения движения имеют вид:

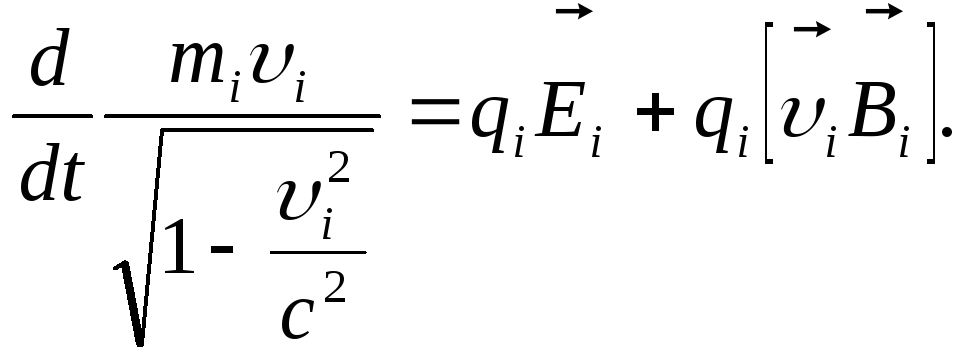. (5.25)

Умножим это выражение на , получим выражение для энергии

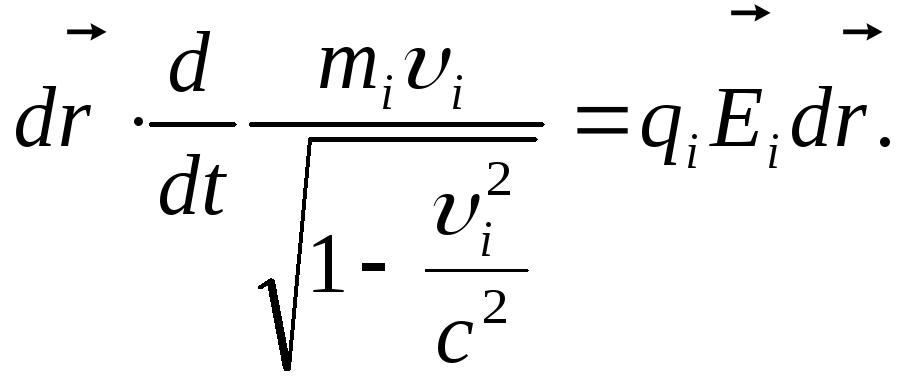
В правой части этого выражения стоит работа силы Лоренца. Она совершается только электрической составляющей этой силы, так как магнитная составляющая равна нулю ( векторы иколлинеарны).

Левую часть преобразуем с помощью тождества

.

Действительно, , тогда в левой части

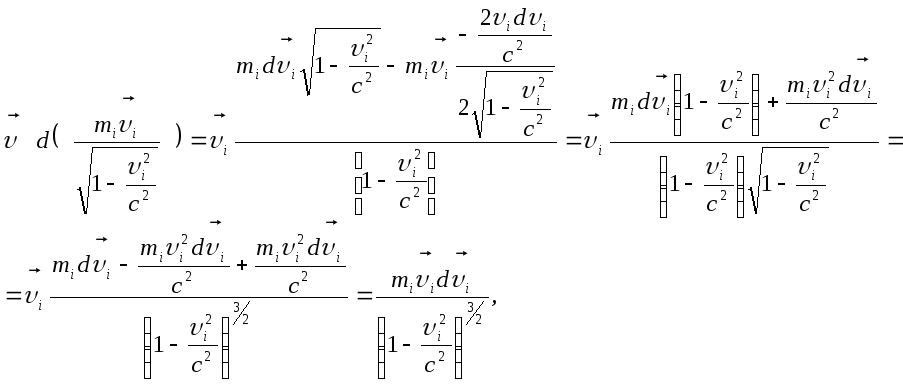
в правой части

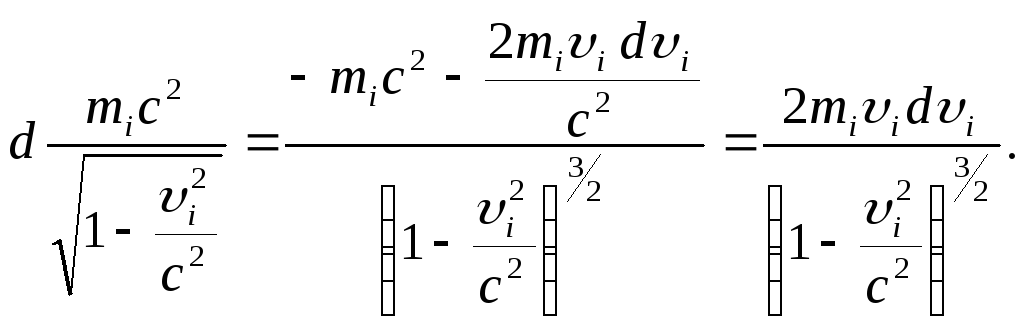
Тогда окончательно получаем

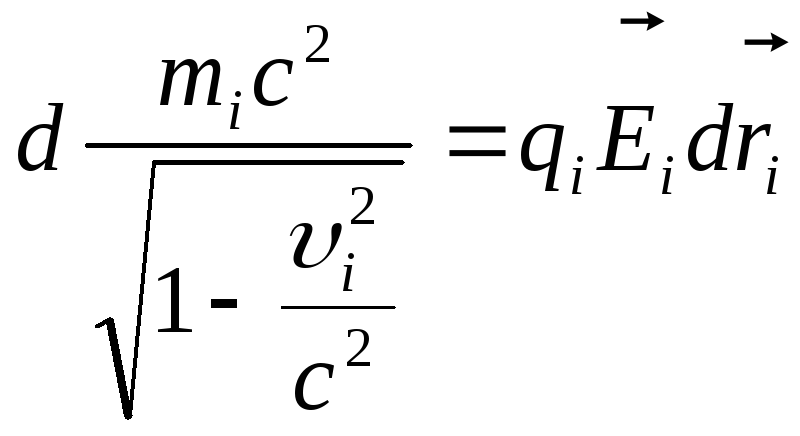
• элементарная работа силы Лоренца равна приросту релятивистской кинетической энергии заряженной материальной точки.

Просуммируем теперь элементарные работы по всем точкам системы и разделим на dt:

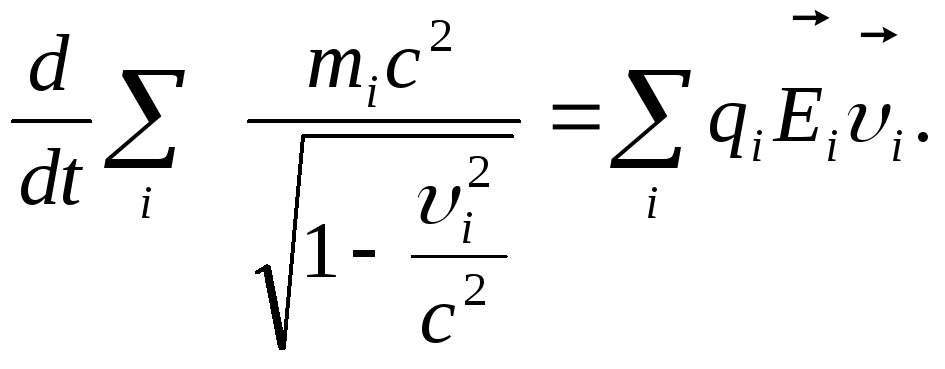(5.26)

( здесь на dt разделили левую и правую части).

Формула (5.23) выражает теорему об изменении энергии системы материальных точек в единицу времени за счет работы поля, совершенной над ними. Выведенная формула для точечного заряда обобщается и на случай непрерывно распределенного в пространстве заряда. Для работы поля в единицу времени имеем:

причем - плотность тока,- заряд одного носителя,- число носителей в единице объема. Тогда

. (5.27)

Мощность, заключенная в единице объема ( плотность мощности) равна

Итак, за счет работы поля изменяется кинетическая энергия находящихся в поле заряженных частиц. При этом энергия поля превращается в кинетическую энергию частиц.